Kőnig's lemma
|
Read other articles:

Will ForteForte di WonderCon tahun 2015LahirOrville Willis Forte IV17 Juni 1970 (umur 53)Alameda County, California, Amerika SerikatNama lainOrville ForteAlmamaterUniversitas California, Los AngelesPekerjaanAktor, pelawak, penulis, produserTahun aktif1997–sekarang Orville Willis Forte IV (/ˈfɔːrteɪ/;[1] lahir 17 Juni 1970) adalah aktor, pelawak, penulis dan produser asal Amerika Serikat. Perannya termasuk menjadi anggota di Saturday Night Live, serta pembuat dan bint…

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁地�…

Questa voce o sezione sull'argomento società calcistiche è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. Football Club ParabiagoCalcio Piccolo…

Canadian peace activist For other uses, see Russow. This biography of a living person needs additional citations for verification. Please help by adding reliable sources. Contentious material about living persons that is unsourced or poorly sourced must be removed immediately from the article and its talk page, especially if potentially libelous.Find sources: Joan Russow – news · newspapers · books · scholar · JSTOR (September 2016) (Learn how and when to…

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Grand Canal Shoppes – berita · surat kabar · buku · cendekiawan · JSTOR (Januari 2016) Grand Canal ShoppesLokasiParadise, NevadaAlamatLas Vegas BoulevardLas Vegas, NevadaTanggal dibuka1999PengembangLas Vegas San…

Soviet military commander (1896–1937) In this name that follows Eastern Slavic naming customs, the patronymic is Emmanuilovich and the family name is Yakir. Iona YakirBirth nameIona Emmanuilovich YakirBorn(1896-08-03)3 August 1896 Kishinev, Bessarabia, Imperial RussiaDied12 June 1937(1937-06-12) (aged 40) Moscow, Russian SFSR, Soviet UnionAllegiance Russian SFSR Soviet UnionService/branch Red ArmyYears of service1918–1937Rank Komandarm 1st rankUnit45th Rifle Division, 58th Rifl…

Beberapa atau seluruh referensi dari artikel ini mungkin tidak dapat dipercaya kebenarannya. Bantulah dengan memberikan referensi yang lebih baik atau dengan memeriksa apakah referensi telah memenuhi syarat sebagai referensi tepercaya. Referensi yang tidak benar dapat dihapus sewaktu-waktu. SMK KARTIKATAMA 1 METROInformasiDidirikan13 Januari 1987JenisSMK SwastaKepala SekolahSujonoRentang kelasX-XIIKurikulumKTSPAlamatLokasiJalan Kapten P.Tendean, Kecamatan margorejo, Metro, Lampung, Indonesi…

2014 American filmTekken 2: Kazuya's RevengeSingaporan theatrical release posterDirected byWych KaosWritten by Nicole Jones Steven Paul Based onTekkenby Bandai Namco GamesProduced by Steven Paul Pimol Srivikorn Starring Kane Kosugi Cary-Hiroyuki Tagawa Rade Šerbedžija Gary Daniels Kelly Wenham CinematographyWych KaosEdited by Vance Null Robert Ferretti Music byMisha SegalProductioncompanyCrystal Sky PicturesDistributed bySP DistributionRelease dates August 6, 2014 (2014-08-06)&#…

American football player (born 1983) This article is about the former football running back. For his son and current running back, see Frank Gore Jr. American football player Frank GoreGore with the San Francisco 49ers in 2012San Francisco 49ersPosition:Football personnel advisorPersonal informationBorn: (1983-05-14) May 14, 1983 (age 41)Miami, Florida, U.S.Height:5 ft 9 in (1.75 m)Weight:212 lb (96 kg)Career informationHigh school:Coral Gables Senior (Coral Gables,…

Dam in Thrissur, KeralaPeringalkuthu DamShutter of Peringalkuthu DamLocation of Peringalkuthu Dam in IndiaShow map of IndiaPeringalkuthu Dam (Kerala)Show map of KeralaOfficial namePeringalkuthu DamLocationChalakudy, Thrissur, KeralaCoordinates10°18′55″N 76°38′04″E / 10.3152°N 76.6344°E / 10.3152; 76.6344Construction began1949Opening date15 May 1957Operator(s)Kerala State Electricity BoardDam and spillwaysImpoundsChalakkudi RiverHeight23 metresLength2…

Pour les articles homonymes, voir Madison. Dolley Madison Dolley Madison, en 1818. Première dame des États-Unis 4 mars 1809 – 4 mars 1817(8 ans) Prédécesseur Martha Jefferson Randolph Successeur Elizabeth Monroe Biographie Nom de naissance Dorothea Payne Todd Madison Date de naissance 20 mai 1768 Lieu de naissance Comté de Guilford, province de Caroline du Nord, Treize colonies Date de décès 12 juillet 1849 (à 81 ans) Lieu de décès Washington, D.C., États-Unis Co…

† Большая гавайская древесница Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Завр…

Indian theoretical physicist (born 1929) Asoke Nath MitraAsoke Nath Mitra at Delhi University in April 1985 on his 56th BirthdayBorn(1929-04-15)April 15, 1929Rajshahi, Rajshahi Division, Bengal Province, British India (modern-day Bangladesh)Died(2022-11-26)November 26, 2022 (aged 93)New Delhi, IndiaAlma materDelhi University (PhD), India, Cornell University (PhD) United StatesKnown forTheoretical Nuclear Physics, Particle Physics, Quantum Field TheoryAwardsBhatnagar AwardScientific car…

Ethnological Museum of BerlinLocation of Ethnological Museum in Berlin, GermanyShow map of BerlinEthnological Museum of Berlin (Germany)Show map of GermanyFormer nameMuseum für Völkerkunde Berlin-DahlemEstablishedOriginal in 1873, new building in 1886, and after World War II rebuilt in present form in 1970LocationMitteCoordinates52°31′03″N 13°24′10″E / 52.5175°N 13.402778°E / 52.5175; 13.402778TypeEthnologicalDirectorViola KönigWebsiteEthnologisches Museum …

SaloméPosterSutradaraCharles BryantProduserAlla NazimovaDitulis olehOscar WildeNatacha RambovaPemeranAlla NazimovaMitchell LewisRose DioneEarl SchenckArthur JasmineNigel De BrulierFrederick PetersLouis DumarSinematograferCharles Van EngerDistributorNazimova ProductionsTanggal rilis 15 Februari 1923 (1923-02-15) Durasi74 menitNegaraAmerika SerikatBahasaAntarjudul InggrisAnggaran$350,000 Salomé (1923), sebuah film bisu garapan Charles Bryant dan dibintangi oleh Alla Nazimova, adalah sebuah …

The 91st United States Congress began on January 3, 1969. There were 12 new senators (four Democrats, eight Republicans) and 38 new representatives (19 Democrats, 19 Republicans), as well as one new delegate (a Democrat), at the start of the first session. Additionally, four senators (two Democrats, two Republicans) and 14 representatives (seven Democrats, seven Republicans) took office on various dates in order to fill vacancies during the 91st Congress before it ended on January 3, 1971. Due t…

Minor Anglo-Saxon kingdom in eastern England The kingdom of Lindsey The Kingdom of Lindsey or Linnuis (Old English: Lindesege) was a lesser Anglo-Saxon kingdom, which was absorbed into Northumbria in the 7th century. The name Lindsey derives from the Old English toponym Lindesege, meaning Isle of Lind. Lindum Colonia was the Roman name of the settlement which is now the City of Lincoln in Lincolnshire. (Lindum Colonia was shortened in Old English to Lindocolina and then Lincylene.)[1] Li…

India in Bangladesh in 2014 Bangladesh IndiaDates 15 June – 19 June 2014Captains Mushfiqur Rahim Suresh RainaOne Day International seriesResults India won the 3-match series 2–0Most runs Mushfiqur Rahim (70) Robin Uthappa (69)Most wickets Taskin Ahmed (7) Stuart Binny (6)Player of the series Stuart Binny (Ind) The Indian national cricket team toured Bangladesh from 15 to 19 June 2014 to play a three-match One Day International (ODI) series against the Bangladesh national cr…
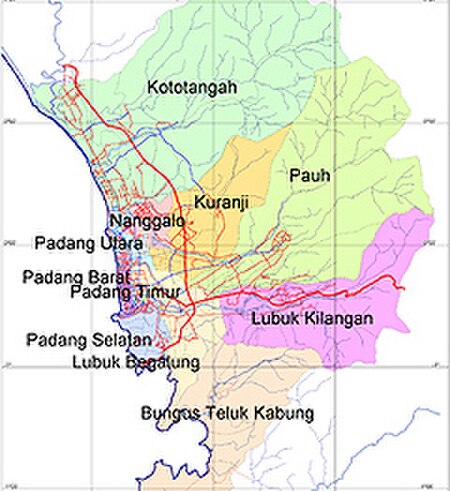
Wilayah administratif kota Padang. Secara geografi kota Padang terletak di pesisir pantai barat pulau Sumatra, dengan garis pantai sepanjang 84 km. Luas keseluruhan Kota Padang adalah 694,96 km², dan lebih dari 60% dari luas tersebut, sekitar ± 434,63 km² merupakan daerah perbukitan yang ditutupi hutan lindung, sementara selebihnya merupakan daerah efektif perkotaan. Sedangkan keadaan topografi kota ini bervariasi, 49,48% luas wilayah daratan Kota Padang berada pada wilayah kemiringan lebih d…

Castle in England that gave its name to the nearby town of the same name This article is about a castle. For the town of the same name in which it is situated, see Barnard Castle. Barnard Castle above the River Tees A plan of the castle from J. D. Mackenzie's The Castles of England: their story and structure[1] Painting of Barnard Castle, by J. M. W. Turner (c. 1825) Barnard Castle (grid reference NZ04911641) is a ruined medieval castle situated in the town of the same name in County Dur…

























