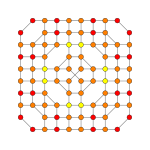
7-demicube
Orthogonal projections in D7 Coxeter plane
In seven-dimensional geometry , a hexic 7-cube is a convex uniform 7-polytope , constructed from the uniform 7-demicube . There are 16 unique forms.
Hexic 7-cube
Cartesian coordinates
The Cartesian coordinates for the vertices of a hexic 7-cube centered at the origin are coordinate permutations:
(±1,±1,±1,±1,±1,±1,±3) with an odd number of plus signs.
Images
Hexicantic 7-cube
Images
Hexiruncic 7-cube
Images
Hexisteric 7-cube
Images
Hexipentic 7-cube
Images
Hexiruncicantic 7-cube
Images
Hexistericantic 7-cube
Images
Hexipenticantic 7-cube
Images
Hexisteriruncic 7-cube
Images
Hexipentiruncic 7-cube
Images
Hexipentisteric 7-cube
Images
Hexisteriruncicantic 7-cube
Images
Hexipentiruncicantic 7-cube
Images
Hexipentisteriruncic 7-cube
Images
Hexipentistericantic 7-cube
Images
Hexipentisteriruncicantic 7-cube
Images
This polytope is based on the 7-demicube , a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 95 uniform polytopes with D7 symmetry, 63 are shared by the BC7 symmetry, and 32 are unique:
D7 polytopes
t0 (141 )
t0,1 (141 )
t0,2 (141 )
t0,3 (141 )
t0,4 (141 )
t0,5 (141 )
t0,1,2 (141 )
t0,1,3 (141 )
t0,1,4 (141 )
t0,1,5 (141 )
t0,2,3 (141 )
t0,2,4 (141 )
t0,2,5 (141 )
t0,3,4 (141 )
t0,3,5 (141 )
t0,4,5 (141 )
t0,1,2,3 (141 )
t0,1,2,4 (141 )
t0,1,2,5 (141 )
t0,1,3,4 (141 )
t0,1,3,5 (141 )
t0,1,4,5 (141 )
t0,2,3,4 (141 )
t0,2,3,5 (141 )
t0,2,4,5 (141 )
t0,3,4,5 (141 )
t0,1,2,3,4 (141 )
t0,1,2,3,5 (141 )
t0,1,2,4,5 (141 )
t0,1,3,4,5 (141 )
t0,2,3,4,5 (141 )
t0,1,2,3,4,5 (141 )
Notes
References
H.S.M. Coxeter :
H.S.M. Coxeter, Regular Polytopes , 3rd Edition, Dover New York, 1973
Kaleidoscopes: Selected Writings of H.S.M. Coxeter , edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
(Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
(Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II , [Math. Zeit. 188 (1985) 559-591]
(Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III , [Math. Zeit. 200 (1988) 3-45] Norman Johnson Uniform Polytopes , Manuscript (1991)
N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs , Ph.D. Klitzing, Richard. "7D uniform polytopes (polyexa)" .
External links