|
Cavitation numberThere are three dimensionless numbers that may be referred to as the cavitation number in various scenarios: the cavitation number for hydrodynamic cavitation, the Thoma number for cavitation in pumps, and the Garcia-Atance number for ultrasonic cavitation (named after Gonzalo Garcia-Atance Fatjo). Hydrodynamic cavitationThe cavitation number (Ca) can be used to predict hydrodynamic cavitation. It has a similar structure as the Euler number, but a different meaning and use: The cavitation number expresses the relationship between the difference of a local absolute pressure from the vapor pressure and the kinetic energy per volume, and is used to characterize the potential of the flow to cavitate. It is defined as[1] 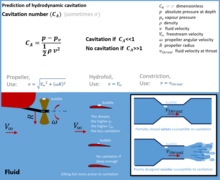
where
The cavitation number serves as one of the primary methods for characterizing cavitation within a fluidic system. Low cavitation number indicates a higher probability of cavitation, while high cavitation number indicates no cavitation. Within a fluid conduit, a pipe or a constraint, as the upstream pressure rises, so does the velocity of the working fluid. However, it's important to note that the increase rate of the square of the velocity greatly surpasses that of the pressure increase. Consequently, the cavitation number exhibits a declining trend with increasing upstream pressure, that is the situation where the system approaches the cavitation. The inception of cavitation occurs when cavitating bubbles first appear within the system, marking the inception cavitation number. This value represents the highest cavitation number observed within the system in presence of cavitation. Researchers often aim to record cavitation inception at relatively low upstream pressures, particularly when they are pursuing non-destructive applications of this phenomenon. As the development of cavitating flow progresses, the cavitation number steadily decreases until the system reaches the point of supercavitation, characterized by the highest achievable velocity and flowrate. Lower cavitation numbers are indicative of more intense cavitating flow. Following supercavitation, the system reaches its fluid-handling limit, even as upstream pressure continues to rise. Consequently, the measured cavitation number embarks on an upward trajectory. This trend is a recurring observation in numerous published articles within the literature.[2] Cavitation in pumpsThe Thoma number () is a dimensionless quantity that can be used to predict cavitation in the suction of a pump. It is named after German engineer Dieter Thoma (1881–1942).[3] It is defined as[4]  Where is the net positive suction head and is the hydraulic head developed by the pump. The fluid will cavitate in the suction of the pump if the Thoma number is smaller than the critical cavitation parameter or the critical Thoma number defined as Where is the net positive suction head required to prevent cavitation. It is a parameter found experimentally for each pump model. See also
References
|
Portal di Ensiklopedia Dunia










