Knotenfläche nennt man in der Physik das feststehende Interferenzminimum einer stehenden Welle in drei Raumdimensionen. Bei stehenden Wellen sind drei Fälle zu unterscheiden:
- Eindimensionale stehende Wellen (z. B. Gitarrensaiten) schwingen um (nulldimensionale) punktförmige Wellen- oder Schwingungsknoten, um Knotenpunkte.
- Zweidimensionale stehende Wellen (z. B. Trommel, Gong oder Plattenglocken) schwingen um (eindimensionale) Knotenlinien. Es treten aber auch Knotenpunkte, die Schnittpunkte von Knotenlinien, auf.
- Dreidimensionale stehende Wellen schwingen um (zweidimensionale) Knotenflächen. Sie können auch Knotenlinien und Knotenpunkte besitzen.
Der Zweig der mathematischen Physik, in dem Knotenpunkte, Knotenlinien und Knotenflächen zum Verständnis eines ein- oder mehrdimensionalen Problems und zur Visualisierung von Funktionen nützlich sind, ist der, bei dem ein (kontinuierliches) gewöhnliches oder verallgemeinertes Eigenwertproblem auftritt, das man zu lösen hat. Vor dieser Aufgabe steht man zum Beispiel bei der Lösung der partiellen Differentialgleichung der freien Schwingung der Akustik und bei der Lösung der stationären Schrödingergleichung der Quantenmechanik und somit in Atomphysik, theoretischer Chemie und Kernphysik.
-
Eindimensionale stehende Welle (als Überlagerung zweier gegenläufiger
Wanderwellen, rot und blau). Nulldimensionale Schwingungsknoten in rot markiert
-
Zweidimensionale stehende Welle.
Die (unbewegten) Knotenlinien haben hier die Form eines X durch den Knotenpunkt, den
Fixpunkt in der Mitte
-
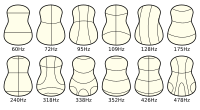
Zweidimensionale stehende Wellen in der Musik:
Chladni-Moden einer (gewölbten) Gitarrendecke mit Knotenlinien und zugehörigen Frequenzen
-
Dreidimensionale stehende Wellen in der Chemie:
Aufenthaltswahrscheinlichkeitsdichten der ersten (1s) und zweiten (2s, 2p)
Elektronenschale.
Die Knotenflächen der
2p-Orbitale sind als Einschnürungen zu erkennen.
-
Zweidimensionale Knotenflächen an der stehenden Welle des Abgasstrahls eines
Nachbrenners
Siehe auch