Ausgezeichnete Punkte im Dreieck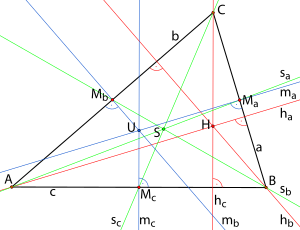

Umkreismittelpunkt (blau), Schwerpunkt (grün) und Höhenschnittpunkt (rot) liegen auf einer Geraden

In der Geometrie versteht man unter den ausgezeichneten Punkten (auch: merkwürdigen Punkten oder Zentren) eines Dreiecks in erster Linie die folgenden vier Punkte:

• den Höhenschnittpunkt H (Schnittpunkt der Höhen),
• den Umkreismittelpunkt U (Schnittpunkt der Mittelsenkrechten (Seitensymmetralen)),
• den Schwerpunkt S (Schnittpunkt der Seitenhalbierenden (Schwerlinien)) und
• den Inkreismittelpunkt I (Schnittpunkt der Winkelhalbierenden (Winkelsymmetralen)).

Die drei erstgenannten Schnittpunkte (H, U und S) liegen immer auf einer Geraden, der eulerschen Geraden. Auf ihr, und zwar in der Mitte zwischen H und U, liegt auch der Mittelpunkt des Feuerbachkreises.

Weitere Punkte nach der Encyclopedia of Triangle Centers

Dreieck mit den „klassischen“ ausgezeichneten Punkten und der eulerschen Geraden

Neben den vier „klassischen“ ausgezeichneten Punkten eines Dreiecks (Schwerpunkt, Umkreismittelpunkt, Inkreismittelpunkt, Höhenschnittpunkt), die schon in der Antike bekannt waren, wurden in den letzten Jahrhunderten viele weitere Punkte gefunden und untersucht. Clark Kimberlings Encyclopedia of Triangle Centers (siehe Weblink) führt mehr als 65.000 (Stand 27. August 2024) besondere Punkte und ihre bislang bekannten Eigenschaften auf. Die in diesem Verzeichnis eingeführte Standardbezeichnung, bestehend aus dem Buchstaben X und einem Index, wird heute in vielen Abhandlungen zur Dreiecksgeometrie verwendet. Die folgende Tabelle nennt einige wichtige Beispiele:

Ausgezeichnete Punkte im Dreieck
Inkreismittelpunkt	${\displaystyle X_{1}}$
Schwerpunkt	${\displaystyle X_{2}}$
Umkreismittelpunkt	${\displaystyle X_{3}}$
Höhenschnittpunkt (Orthozentrum)	${\displaystyle X_{4}}$
Mittelpunkt des Feuerbach-Kreises	${\displaystyle X_{5}}$
Lemoine-Punkt (Symmedianenpunkt, Grebe-Punkt)	${\displaystyle X_{6}}$
Gergonne-Punkt	${\displaystyle X_{7}}$
Nagel-Punkt	${\displaystyle X_{8}}$
Mittenpunkt	${\displaystyle X_{9}}$
Spieker-Punkt (Spieker-Zentrum)	${\displaystyle X_{10}}$
Feuerbachpunkt (Berührungspunkt von Inkreis und Feuerbachkreis)	${\displaystyle X_{11}}$
1. Fermat-Punkt (u. a. kürzester Abstand zu allen Eckpunkten)	${\displaystyle X_{13}}$
2. Fermat-Punkt	${\displaystyle X_{14}}$
1. isodynamischer Punkt	${\displaystyle X_{15}}$
2. isodynamischer Punkt	${\displaystyle X_{16}}$
1. Napoleon-Punkt	${\displaystyle X_{17}}$
2. Napoleon-Punkt	${\displaystyle X_{18}}$
Clawson-Punkt	${\displaystyle X_{19}}$
Longchamps-Punkt	${\displaystyle X_{20}}$
Schiffler-Punkt	${\displaystyle X_{21}}$
Exeter-Punkt	${\displaystyle X_{22}}$
Bevan-Punkt	${\displaystyle X_{40}}$
Kosnita-Punkt	${\displaystyle X_{54}}$
Steiner-Punkt	${\displaystyle X_{99}}$
Isoperimetrischer Punkt	${\displaystyle X_{175}}$
Punkt des gleichen Umwegs	${\displaystyle X_{176}}$
1. Vecten-Punkt	${\displaystyle X_{485}}$
2. Vecten-Punkt	${\displaystyle X_{486}}$

Verwandte Themen

Neben Einzelpunkten lassen sich einem Dreieck auch verschiedene Tupel von Punkten zuordnen:

• Morley-Dreieck
• Napoleon-Dreieck
• Höhenfußpunktdreieck
• Brocard-Punkte
• Johnson-Dreieck
• Kiepert-Dreieck

Spezielle Kreise sind:

• Umkreis, Inkreis, Ankreise
• Feuerbach-Kreis (Neun-Punkte-Kreis)
• Lamoen-Kreis
• Taylor-Kreis
• Johnson-Kreise

Weitere spezielle Kegelschnitte sind:

• Kiepert-Hyperbel
• Steiner-Ellipse
• Steiner-Inellipse

Literatur

• Ilka Agricola, Thomas Friedrich: Elementargeometrie. 2. Auflage. Vieweg+Teubner, Wiesbaden 2009, ISBN 978-3-8348-0576-8.
• Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, Berlin 2007, ISBN 978-3-540-49327-3.

Weblinks

• Clark Kimberling’s Encyclopedia of Triangle Centers faculty.evansville.edu
• Florian Modler: Merkwürdige Punkte und Linien am Dreieck. In: matheplanet.com.
• Arndt Brünner: Interaktive Darstellung aller oben genannten Punkten und Objekten am Dreieck, arndt-bruenner.de