|
سعة كهربية
السعة الكهربائية في الموصل الكهربائي هي خاصية تعكس مدى قدرته على حفظ شحنة كهربائية والنبيطة الإلكترونية الأكثر استعمالا في هذه المجال هي المكثف الذي يمكنه تزويد أي دائرة كهربائية بالسعة عن طريق خزن الطاقة داخل مجال كهربائي بين جسمين موصلين.[5][6][7] والسعة هي نسبة كمية الشحنة الكهربائية المخزنة على الموصل إلى فرق الجهد الكهربائي. هناك نوعان من المفاهيم وثيقة الصلة بالسعة: السعة الذاتية والسعة المتبادلة.[8] :237–238أي جسم يمكن أن يكون مشحونًا كهربائيًا يظهر سعة ذاتية. في هذه الحالة، يتم قياس فرق الجهد الكهربائي بين الجسم والأرض. تحمل المادة ذات السعة الذاتية الكبيرة شحنة كهربائية عند فرق جهد معين أكثر من تلك ذات السعة المنخفضة. تعتبر فكرة السعة المتبادلة مهمة بشكل خاص لفهم عمليات المكثف، وهو أحد المكونات الإلكترونية الخطية الأولية الثلاثة (جنبًا إلى جنب مع المقاومات والمحاثات). في مكثف نموذجي، يتم استخدام موصلين لفصل الشحنة الكهربائية، حيث يكون أحدهما موجبًا والآخر مشحونًا سالبًا، ولكن النظام به شحنة إجمالية تساوي صفرًا. النسبة في هذه الحالة هي مقدار الشحنة الكهربائية على أي من الموصلات وفرق الجهد هو المقاس بين الموصلين. السعة هي وظيفة فقط من هندسة تصميم (منطقة سبيل المثال لوحات والمسافة بينهما) والسماحية لل عازلة المواد بين لوحات للمكثف. بالنسبة للعديد من المواد العازلة للكهرباء، تكون السماحية وبالتالي السعة مستقلة عن فرق الجهد بين الموصلات والشحنة الكلية عليها. وحدة السعة في النظام الدولي للوحدات هي فاراد (الرمز:F)، التي سميت على اسم الفيزيائي الإنجليزي مايكل فاراداي. مكثف 1 فاراد، عند شحنه بـ 1 كولوم من الشحنة الكهربائية، يكون له فرق جهد قدره 1 فولت بين لوحاته.[9] يُطلق على مقلوب السعة اسم المرونة. اكتشف السعة داخل الدائرة الكهربائية عام 1745 م عن طريق عالمين مختلفين داخل معملي مختصين بعلم الكهربية الساكنة حينها اكتشفا إمكانية حفظ الطاقة لفترة زمنية داخل الدائرة الكهربائية وبالتحديد داخل نبيطة معينة تسمى الآن قارورة ليدن وهي أول مكثف تم اختراعه. يرمز للسعة بالرمز و تساوي السعة
وحدة قياس السعة حسب النظام الدولي للوحدات هي فاراد وتساوي (كولوم لكل فولت و القانون العام لحساب قيمة الطاقة المخزنة داخل مكثف ما بما أن الطاقة المخزنة تساوي مقدار الشغل المبذول لخزنها هو:
حيث:
السعة الذاتيةفي الدوائر الكهربائية، مصطلح السعة هو اختصار للسعة المتبادلة بين موصلين متجاورين، مثل لوحتين من المكثف. ومع ذلك، بالنسبة للموصل المعزول، توجد أيضًا خاصية تسمى السعة الذاتية، وهي مقدار الشحنة الكهربائية التي يجب إضافتها إلى موصل معزول لرفع جهده الكهربائي بوحدة واحدة (أي واحد فولت، في معظم أنظمة القياس).[10] النقطة المرجعية لهذه الإمكانية هي كرة نظرية مجوفة موصلة، ذات نصف قطر لانهائي، مع وجود موصل متمركز داخل هذا المجال. رياضيا، يتم تحديد السعة الذاتية للموصل بواسطة
أي ان q هي التهمة المحتجزة على الموصل، هو الجهد الكهربائي، σ هي كثافة شحنة السطح. dS هو عنصر متناهي الصغر للمساحة على سطح الموصل، r هو الطول من dS إلى نقطة ثابتة M على الموصل باستخدام هذه الطريقة، تكون السعة الذاتية لمجال موصل نصف قطر R هي:[11]
مثال على قيم السعة الذاتية:
تسمى السعة البينية للملف أحيانًا السعة الذاتية،[13] ولكن هذه ظاهرة مختلفة. إنها في الواقع سعة متبادلة بين الدورات الفردية للملف وهي شكل من أشكال السعة الشاردة أو الطفيلية. تعتبر هذه السعة الذاتية من الاعتبارات المهمة عند الترددات العالية: فهي تغير مقاومة الملف وتؤدي إلى صدى موازٍ. يعد هذا تأثيرًا غير مرغوب فيه في العديد من التطبيقات ويضع حدًا أعلى للتردد للتشغيل الصحيح للدائرة. السعة المتبادلةالشكل الشائع هو المكثف المتوازي اللوح، والذي يتكون من لوحين موصلين معزولين عن بعضهما البعض، وعادة ما يكونان عبارة عن مادة عازلة للكهرباء. في مكثف اللوح المتوازي، تكون السعة متناسبة تقريبًا جدًا مع مساحة سطح الألواح الموصلة وتتناسب عكسيًا مع المسافة الفاصلة بين الألواح. إذا كانت الشحنات على الألواح هي q+ وq- وV يعطي الجهد بين الألواح، فإن السعة C تعطى بواسطة
والذي يعطي علاقة الجهد / التيار
أي انdv(t)dt هو المعدل اللحظي للتغير في الجهد. يتم العثور على الطاقة المخزنة في مكثف بدمج العمل W:
مصفوفة السعةالمناقشة أعلاه تقتصر على حالة لوحين موصلين، على الرغم من الحجم والشكل التعسفيين. التعريف لا ينطبق عندما يكون هناك أكثر من لوحين مشحونين، أو عندما تكون الشحنة الصافية على اللوحتين غير صفرية. للتعامل مع هذه الحالة، قدم ماكسويل معاملاته المحتملة. إذا تم فرض رسوم على ثلاثة موصلات (شبه مثالية) ، ثم يتم إعطاء الجهد عند الموصل 1 بواسطة
وبالمثل بالنسبة للجهود الأخرى. أظهر هيرمان فون هيلمهولتز والسير ويليام طومسون أن معاملات الجهد متناظرة، بحيث ، إلخ. وبالتالي يمكن وصف النظام من خلال مجموعة من المعاملات المعروفة باسم مصفوفة المرونة أو مصفوفة السعة التبادلية، والتي يتم تعريفها على النحو التالي:
من هذا، السعة المتبادلة بين كائنين يمكن تعريفها [14] عن طريق حل الشحنة الإجمالية Q وباستخدام .
نظرًا لعدم وجود جهاز فعلي يحمل شحنة متساوية تمامًا ومعاكسة على كل من «الصفيحتين»، فإن السعة المتبادلة هي التي يتم الإبلاغ عنها في المكثفات. جمع المعاملات تُعرف بمصفوفة السعة،[15][16][17] وهي معكوس مصفوفة المرونة. المكثفاتتكون سعة غالبية المكثفات المستخدمة في الدوائر الإلكترونية بشكل عام أصغر بعدة مرات من قيمة الفاراد. معظم مفارز مشتركة من السعة المستخدمة اليوم هي مكروفاراد (μF)، نانوفاراد (nF)، بيكوفاراد في رقائق، فيمتفاراد (FF). ومع ذلك، يمكن أن تكون المكثفات الفائقة المصنوعة خصيصًا أكبر بكثير (مثل مئات الفارادات)، ويمكن أن تكون العناصر السعوية الطفيلية أقل من الفيمتوفاراد. في الماضي، تم استخدام وحدات فرعية بديلة في النصوص التاريخية القديمة؛ "mf" و"mfd" للميكروفاراد (µF)؛ "mmf"، "mmfd"، "pfd"، "F" لـ بيكوفاراد(pF)؛ لكنها تعتبر الآن عفا عليها الزمن.[18][19] يمكن حساب السعة إذا كانت هندسة الموصلات وخصائص العزل الكهربائي للعازل بين الموصلات معروفة. يمكن إعطاء تفسير نوعي لهذا على النحو التالي. بمجرد وضع شحنة موجبة في الموصل، تخلق هذه الشحنة مجالًا كهربائيًا، مما يؤدي إلى صد أي شحنة موجبة أخرى يتم نقلها إلى الموصل؛ أي زيادة الجهد اللازم. ولكن إذا كان هناك موصل آخر قريبًا عليه شحنة سالبة، فإن المجال الكهربائي للموصل الموجب الذي يصد الشحنة الموجبة الثانية يضعف (الشحنة الموجبة الثانية تشعر أيضًا بقوة جذب الشحنة السالبة). لذلك بسبب الموصل الثاني بشحنة سالبة، يصبح من الأسهل وضع شحنة موجبة على الموصل الأول الموجب بالفعل والعكس صحيح؛ أي، يتم تخفيض الجهد اللازم. كمثال كمي، ضع في اعتبارك سعة مكثف مكون من لوحين متوازيين كلاهما في المنطقة أ مفصولة بمسافة d إذا كان d صغيرًا بدرجة كافية فيما يتعلق بأصغر وتر من A، فهناك مستوى عالٍ من الدقة:
أي ان
السعة الشاردةالسعة الطفيلية أو السعة الضالة هي التي لا يمكن تجنبها، وعادة غير المرغوب فيها السعة الموجودة بين أجزاء من مكونات إلكترونية أو الدائرة ببساطة بسبب قربها من بعضها البعض. عندما يكون موصلان كهربائيان بجهد كهربائي مختلفين قريبين من بعضهما البعض، فإن المجال الكهربائي بينهما يتسبب في تخزين الشحنة الكهربائية عليهما؛ هذا التأثير هو السعة الطفيلية. يمكن أن يعمل أي موصلين متجاورين كمكثف، على الرغم من أن السعة صغيرة ما لم تكن الموصلات قريبة من بعضها البعض لمسافات طويلة أو على مساحة كبيرة. تسمى هذه السعة (غير المرغوب فيها في الغالب) الطفيلية أو «السعة الشاردة». يمكن أن تسمح السعة الشاردة للإشارات بالتسرب بين الدوائر المعزولة بطريقة أخرى (وهو تأثير يسمى الحديث المتبادل)، ويمكن أن يكون عاملاً مقيدًا للتشغيل السليم للدوائر عند التردد العالي.يمكن أن تكون السعة الشاردة بين المدخلات والمخرجات في دوائر مكبر الصوت مزعجة لأنها يمكن أن تشكل مسارًا للتغذية المرتدة، مما قد يتسبب في عدم الاستقرار والتذبذب الطفيلي في مكبر الصوت. غالبًا ما يكون من الملائم للأغراض التحليلية استبدال هذه السعة بمزيج من سعة إدخال إلى الأرض وسعة إخراج إلى الأرض؛ غالبًا ما يشار إلى التكوين الأصلي - بما في ذلك سعة الإدخال إلى الإخراج - على أنه تكوين pi. يمكن استخدام نظرية ميلر لإحداث هذا الاستبدال: تنص على أنه إذا كانت نسبة كسب عقدتين هي 1 / K، فيمكن استبدال معاوقة Z التي تربط العقدتين بـ Z / (1−K) بين العقدة الأولى والأرض وKZ/ (K.−1) مقاومة بين العقدة الثانية والأرض. نظرًا لأن الممانعة تختلف عكسيًا مع السعة، يتم استبدال السعة الداخلية، C، بسعة KC من الإدخال إلى الأرض وسعة (K−1) C/K من الإخراج إلى الأرض. عندما يكون كسب الإدخال إلى الإخراج كبيرًا جدًا، تكون المعاوقة المكافئة للإدخال إلى الأرض صغيرة جدًا بينما تكون مقاومة الخرج إلى الأرض مساوية بشكل أساسي للمقاومة الأصلية (المدخلات إلى المخرجات). سعة الموصلات ذات الأشكال البسيطةيؤدي حساب سعة نظام ما إلى حل معادلة لابلاس ∇ 2 φ = 0 مع φ المحتملين المستمر على السطح الأبعاد من الموصلات جزءا لا يتجزأ من الفراغ. يتم تبسيط هذا من خلال التماثلات. لا يوجد حل من حيث الوظائف الأولية في الحالات الأكثر تعقيدًا. بالنسبة لحالات المستوى، يمكن استخدام الوظائف التحليلية لتعيين أشكال هندسية مختلفة لبعضها البعض. انظر أيضًا رسم خرائط شوارتز - كريستوفل.
تخزين الطاقةالطاقة (التي تقاس ب الجول) المخزنة في مكثف تساوي العمل المطلوب لدفع الشحنات في مكثف، أي إلى توجيه الاتهام له. لنفترض أن مكثف السعة C يحمل شحنة q+ على أحد اللوحين وq- على الأخرى. يتطلب نقل عنصر صغير من الشحنة d q من لوحة إلى أخرى مقابل فرق الجهد V = q/C الشغل d W :
حيث W هي الشغل المقاس بالجول، q هي الشحنة المقاسة بالكولوم وC هي السعة المقاسة بالفاراد. يمكن إيجاد الطاقة المخزنة في مكثف بدمج هذه المعادلة. بدءًا من سعة غير مشحونة (q = 0) وتحريك الشحنة من لوحة إلى أخرى حتى يتم شحن الألواح Q+ وQ- يتطلب الشغلW:
أنظمة النانوقد تختلف سعة المكثفات النانوية العازلة مثل النقاط الكمومية عن الصيغ التقليدية للمكثفات الأكبر. على وجه الخصوص، فإن فرق الجهد الكهروستاتيكي الذي تختبره الإلكترونات في المكثفات التقليدية محدد جيدًا ومثبتًا من خلال شكل وحجم الأقطاب المعدنية بالإضافة إلى العدد الكبير إحصائيًا من الإلكترونات الموجودة في المكثفات التقليدية. في المكثفات النانوية، يتم تحديد الإمكانات الكهروستاتيكية التي تتعرض لها الإلكترونات من خلال عدد ومواقع جميع الإلكترونات التي تساهم في الخصائص الإلكترونية للجهاز. في مثل هذه الأجهزة، قد يكون عدد الإلكترونات صغيرًا جدًا، وبالتالي فإن التوزيع المكاني الناتج للأسطح متساوية الجهد داخل الجهاز معقد للغاية. أجهزة الإلكترون الواحدإن سعة الجهاز أحادي الإلكترون المتصل أو «المغلق» هي ضعف سعة جهاز إلكتروني واحد غير متصل أو «مفتوح».[28] يمكن إرجاع هذه الحقيقة بشكل أساسي إلى الطاقة المخزنة في الجهاز أحادي الإلكترون الذي يمكن تقسيم طاقة تفاعل «الاستقطاب المباشر» بشكل متساوٍ إلى تفاعل الإلكترون مع الشحنة المستقطبة على الجهاز نفسه بسبب وجود الإلكترون ومقدار الطاقة الكامنة المطلوبة لتشكيل الشحنة المستقطبة على الجهاز (تفاعل الشحنات في مادة عازلة للجهاز مع الجهد الناتج عن الإلكترون).[29] عدد قليل من الأجهزة الإلكترونيةيتضمن اشتقاق «السعة الكمومية» لجهاز قليل الإلكترونات الجهد الكيميائي الديناميكي الحراري لنظام الجسيمات N المعطى بواسطة
يمكن الحصول على شروط طاقتها كحلول لمعادلة شرودنغر. تعريف السعة،
مع الفارق المحتمل
يمكن تطبيقها على الجهاز مع إضافة أو إزالة الإلكترونات الفردية، و . ثم
هي «السعة الكمومية» للجهاز.[30] يمكن كتابة هذا التعبير عن «السعة الكمومية» كـ
والذي يختلف عن التعبير الاصطلاحي الموصوف في المقدمة حيث ، الطاقة الكامنة الكهروستاتيكية المخزنة،
بمعامل 1/2 مع . ومع ذلك، في إطار التفاعلات الكهروستاتيكية الكلاسيكية البحتة، فإن ظهور عامل 1/2 هو نتيجة التكامل في الصيغة التقليدية،
وهو مناسب منذ ذلك الحين للأنظمة التي تتضمن إما العديد من الإلكترونات أو الأقطاب الكهربائية المعدنية، ولكن في أنظمة قليلة الإلكترون، . يصبح التكامل عمومًا مجموعًا. يمكن للمرء أن يجمع بشكل تافه بين تعبيرات السعة وطاقة التفاعل الكهروستاتيكي، و على التوالي للحصول على،
التي تشبه السعة الكمومية. تم الإبلاغ عن اشتقاق أكثر صرامة في الأدبيات.[31] على وجه الخصوص، للتحايل على التحديات الرياضية للأسطح متساوية الجهد المعقدة مكانيًا داخل الجهاز، يتم استخدام متوسط الجهد الكهروستاتيكي الذي يعاني منه كل إلكترون في الاشتقاق. تُفهم الاختلافات الرياضية الظاهرة بشكل أساسي على أنها الطاقة الكامنة، ، للجهاز المعزول (السعة الذاتية) ضعف ما تم تخزينه في جهاز «متصل» في الحد الأدنى N = 1. مع نمو N بشكل كبير، .[29] وبالتالي، فإن التعبير العام عن السعة هو
في الأجهزة النانوية مثل النقاط الكمومية، غالبًا ما يكون «المكثف» مكونًا معزولًا أو معزولًا جزئيًا داخل الجهاز. الاختلافات الأساسية بين المكثفات النانوية والمكثفات العيانية (التقليدية) هي عدد الإلكترونات الزائدة (ناقلات الشحنة، أو الإلكترونات، التي تساهم في السلوك الإلكتروني للجهاز) وشكل وحجم الأقطاب الكهربائية المعدنية. في الأجهزة النانوية، لا تُظهر الأسلاك النانوية المكونة من ذرات معدنية نفس الخصائص الموصلة مثل نظيراتها المجهرية أو المواد السائبة. السعة في الأجهزة الإلكترونية وأشباه الموصلاتفي الأجهزة الإلكترونية وأشباه الموصلات، يحتوي التيار العابر أو المعتمد على التردد بين المحطات على مكونات التوصيل والإزاحة. يرتبط تيار التوصيل بحاملات الشحنة المتحركة (الإلكترونات، الثقوب، الأيونات، إلخ)، في حين أن تيار الإزاحة ناتج عن مجال كهربائي متغير بمرور الوقت. يتأثر النقل الحامل بالمجالات الكهربائية وعدد من الظواهر الفيزيائية - مثل انجراف الحامل وانتشاره، والحبس، والحقن، والتأثيرات المرتبطة بالتلامس، وتأين الصدمات، إلخ. ونتيجة لذلك، فإن دخول الجهاز يعتمد على التردد، وصيغة كهروستاتيكية بسيطة للسعة لا يمكن تطبيقه. تعريف أكثر عمومية للسعة، يشمل الصيغة الكهروستاتيكية، هو:[32]
أي ان هو دخول الجهاز، و هو التردد الزاوي. بشكل عام، السعة دالة للتردد. عند الترددات العالية، تقترب السعة من قيمة ثابتة، تساوي السعة «الهندسية»، تحددها هندسة المحطات الطرفية ومحتوى العزل الكهربائي في الجهاز. تقدم ورقة بقلم ستيفن لوكس [32] مراجعة للتقنيات العددية لحساب السعة. على وجه الخصوص، يمكن حساب السعة عن طريق تحويل فورييه لتيار عابر استجابة لإثارة جهد شبيه بالخطوة:
السعة السلبية في أجهزة أشباه الموصلاتعادةً ما تكون السعة في أجهزة أشباه الموصلات موجبة. ومع ذلك، في بعض الأجهزة وتحت ظروف معينة (درجة الحرارة، الفولتية المطبقة، التردد إلخ)، يمكن أن تصبح السعة سالبة. تم اقتراح السلوك غير الرتيب للتيار العابر استجابةً لإثارة تشبه الخطوة كآلية للسعة السلبية.[33] تم توضيح واستكشاف السعة السلبية في العديد من الأنواع المختلفة لأجهزة أشباه الموصلات.[34] قياس السعةمقياس السعة عبارة عن قطعة من معدات الاختبار الإلكترونية تستخدم لقياس السعة، بشكل أساسي من المكثفات المنفصلة. بالنسبة لمعظم الأغراض وفي معظم الحالات، يجب فصل المكثف عن الدائرة. تحتوي العديد من أجهزة DVM (عدادات الفولت الرقمية) على وظيفة قياس السعة. تعمل هذه عادةً عن طريق شحن وتفريغ المكثف قيد الاختبار بتيار معروف وقياس معدل ارتفاع الجهد الناتج؛ كلما كان معدل الارتفاع أبطأ، زادت السعة. يمكن لأجهزة DVM عادة قياس السعة من نانوفاراد إلى بضع مئات من الميكروفاراد، لكن النطاقات الأوسع ليست غير عادية. من الممكن أيضًا قياس السعة بتمرير تيار متناوب معروف عالي التردد عبر الجهاز قيد الاختبار وقياس الجهد الناتج عبره (لا يعمل مع المكثفات المستقطبة).  تستخدم الأدوات الأكثر تعقيدًا تقنيات أخرى مثل إدخال المكثف قيد الاختبار في دائرة الجسر. من خلال تغيير قيم الأرجل الأخرى في الجسر (لتحقيق توازن الجسر)، يتم تحديد قيمة المكثف غير المعروف. تضمن طريقة الاستخدام غير المباشر لقياس السعة دقة أكبر. من خلال استخدام توصيلات كلفن وتقنيات التصميم الدقيقة الأخرى، يمكن لهذه الأدوات عادةً قياس المكثفات على مدى من البيكوفاراد إلى الفاراد. انظر أيضًاالمراجع
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia



























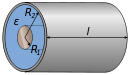















![{\displaystyle {\frac {2\pi \varepsilon \ell }{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a19746fa861b22587cd9fbfcc0ed075187e6dc6a)


























![{\displaystyle C(\omega )=1/(\Delta V)\int _{0}^{\infty }[i(t)-i(\infty )]\cos(\omega t)dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c66901ca0aa9fae98568a289c3e444ed3f5a96f3)