|
Particle swarm optimization Dalam Ilmu komputasi, Particle Swarm Optimization (biasa disingkat: PSO)[1] adalah sebuah metode komputasi yang mengoptimasi suatu masalah dengan menggunakan metode iteratif untuk memperbaiki suatu kandidat solusi dengan ukuran kualitas tertentu. Cara PSO dalam menyelesaikan masalah tersebut adalah dengan menggunakan sebuah populasi yang berisi kandidat-kandidat solusi yang disebut sebagai partikel, dan kemudian menggerakkan partikel-partikel tersebut di dalam ruang pencarian berdasarkan rumus sederhana dalam penentuan posisi dan kecepatan (velocity) tiap partikel. Pergerakan setiap partikel dalam ruang pencarian ini tidak hanya dipengaruhi oleh posisi lokal terbaik yang saat ini diketahui oleh partikel tersebut (local best known position), tetapi pergerakannya juga dipandu menuju posisi terbaik dalam ruang pencarian secara keseluruhan, yang diperbarui seiring dengan ditemukannya posisi yang lebih baik oleh partikel lain. Hal ini diharapkan dapat menggerakkan kawanan atau gerombolan menuju solusi terbaik. PSO awalnya dikaitkan dengan Kennedy, Eberhart, dan Shi[2][3] dan pertama kali dimaksudkam untuk simulasi perilaku sosial,[4] sebagai representasi non natural (stylized representation) dari pergerakan organisme kawanan burung atau gerombolan ikan. Algoritmanya disederhanakan dan diamati untuk melakukan optimasi. Buku karya Kennedy dan Eberhart[5] menjelaskan banyak aspek filosofis dari PSO dan kecerdasan gerombolan. Sebuah survei mendalam mengenai aplikasi PSO dibuat oleh Poli.[6][7] Baru-baru ini, sebuah kajian komprehensif mengenai karya-karya teoretis dan eksperimental mengenai PSO telah diterbitkan oleh Bonyadi dan Michalewicz.[1] PSO adalah salah satu algoritma metaheuristik, yang artinya PSO hanya membuat sedikit atau bahkan tidak ada asumsi apapun mengenai masalah yang dioptimalkan dan mampu menelusuri ruang kandidat solusi yang sangat luas. Selain itu, PSO tidak menggunakan gradien dari masalah yang sedang dioptimalkan, yang berarti PSO tidak mengharuskan masalah pengoptimalan merupakan fungsi terdiferensialkan sebagaimana yang diharuskan dalam metode pengoptimalan klasik, seperti penurunan gradien dan metode quasi-newton. Meskipun begitu, PSO, sebagaimana algoritma metaheuristik lainnya, tidak dapat menjamin untuk menemukan solusi optimal global. AlgoritmaVarian dasar dari algoritma PSO bekerja dengan menggunakan sebuah populasi (disebut kawanan atau gerombolan) dari kandidat solusi (disebut partikel). Partikel-partikel tersebut bergerak di dalam ruang pencarian mengikut pada beberapa rumus sederhana.[8] Pergerakan partikel dipandu oleh posisi terbaik (local best known position) mereka sendiri dan posisi terbaik seluruh kawanan dalam ruang pencarian. Ketika posisi yang lebih baik ditemukan, posisi terseut akan memandu pergerakan kawanan. Proses ini akan terus diulang dan diharapkan, tetapi tidak menjamin; solusi yang memuaskan akan ditemukan di akhir iterasi. Secara formal, misalkan f: ℝn → ℝ adalah fungsi biaya yang akan diminimalkan. Fungsi ini mengambil satu kandidat solusi sebagai parameter dalam bentuk vektor baris dari bilangan riil dan menghasilkan keluaran sebuah bilangan riil yang menunjukkan nilai fungsi objektif dari kandidat solusi yang diberikan. Nilai gradien dari f tidak diketahui. Tujuan dari permasalahan ini adalah menemukan sebuah solusi a yang mana f(a) ≤ f(b) untuk semua b di dalam ruang pencarian solusi, yang berarti a adalah minimal global. Misalkan S adalah jumlah partikel dalam kawanan yang setiap partikel tersebut memiliki satu nilai posisi xi ∈ ℝn dalam ruang pencarian solusi dan satu nilai kecepatan vi ∈ ℝn. Misal, pi adalah posisi terbaik yang diketahui partikel i dan g adalah posisi terbaik yang diketahui seluruh kawanan. Maka, algoritma PSO dasar yang dapat meminimalkan fungsi biaya adalah, antara lain:[9] for setiap partikel i = 1, ..., S do
Inisialisasi posisi partikel dengan vektor acak berdasarkan distribusi seragam kontinu: xi ~ U(blo, bup)
Inisialisasi posisi awal partikel menjadi posisi terbaik yang diketahui partikel: pi ← xi
if f(pi) < f(g) then
perbarui posisi terbaik seluruh kawanan: g ← pi
Inisialisasi kecepatan (velocity) partikel: vi ~ U(-|bup-blo|, |bup-blo|)
while kriteria penghentian belum terpenuhi do:
for setiap partikel i = 1, ..., S do
for setiap dimensi d = 1, ..., n do
Pilih angka acak: rp, rg ~ U(0,1)
Perbarui kecepatan partikel: vi,d ← w vi,d + φp rp (pi,d-xi,d) + φg rg (gd-xi,d)
Perbarui posisi partikel: xi ← xi + vi
if f(xi) < f(pi) then
Perbarui posisi terbaik yang diketahui partikel: pi ← xi
if f(pi) < f(g) then
Perbarui posisi terbaik seluruh kawanan: g ← pi
Nilai blo dan bup, masing-masing menunjukkan batas bawah dan batas atas dari ruang pencarian. Parameter w adalah bobot inersia. Sedangkan parameter φp dan φg seringkali disebut sebagai koefisien kognitif dan koefisien sosial. Kriteria penghentian (termination criterion) dapat berupa maksimum jumlah iterasi yang dilakukan atau suatu solusi fungsi objektif yang memuaskan telah ditemukan.[10] Parameter w, φp, dan φg dipilih oleh praktisi yang ketiganya ini dapat mengontrol perilaku dan kemanjuran algoritma PSO (di bawah). Seleksi parameter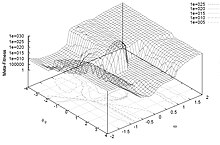 Pemilihan parameter PSO dapat berdampak besar pada kinerja optimasi. Oleh karena itu, pemilihan parameter PSO yang memberikan performa yang baik menjadi subjek dari banyak penelitian.[11][12][13][14][15][16][17][18][19] Untuk mencegah divergensi ("ledakan"), bobot inersia harus lebih kecil dari 1. Dua parameter lainnya dapat diturunkan melalui pendekatan pembatasan (constriction approach),[16] atau dapat dipilih secara bebas, tetapi para ahli menganalisis bahwa domain konvergensi dapat digunakan untuk membatasi parameter-parameter tersebut. Nilai-nilai yang umum digunakan adalah . Parameter PSO juga dapat di-tuning dengan menggunakan pengoptimal lain, sebuah konsep yang dikenal sebagai optimasi-meta,[20][21][22][23] atau bahkan di-tuning selama pengoptimalan, misal, dengan menggunakan logika fuzzy.[24][25] Parameter juga telah di-tuning untuk berbagai skenario pengoptimalan.[26][27] Ketetanggaan dan topologiTopologi dari kawanan mendefinisikan bagaimana subhimpunan partikel dapat digunakan oleh setiap partikel untuk bertukar informasi.[28] Versi dasar algoritma ini menggunakan topologi global sebagai struktur komunikasi pada kawanan.[10] Topologi ini memungkinkan semua partikel untuk berkomunikasi dengan semua partikel lainnya, sehingga seluruh kawanan berbagi posisi terbaik yang sama g' dari sebuah partikel. Namun, pendekatan ini dapat menyebabkan kawanan terjebak ke dalam minimum lokal,[29]. Oleh karena itu, topologi yang berbeda telah digunakan untuk mengontrol aliran informasi di antara partikel. Sebagai contoh, pada topologi lokal, partikel-partikel hanya berbagi informasi dengan sebagian kecil partikel.[10] Sebagian kecil ini dapat berupa sebuah geometri[30] - misalnya "partikel terdekat m" - atau, lebih sering, partikel sosial, yaitu sekumpulan partikel yang tidak bergantung pada jarak apa pun. Dalam kasus seperti itu, varian PSO dikatakan sebagai yang terbaik secara lokal (dibandingkan yang terbaik secara global untuk PSO dasar). Topologi kawanan yang umum digunakan adalah ring atau cincin, yang masing-masing partikel hanya memiliki dua tetangga, tetapi terdapat topologi lainnya.[10] Topologi ini tidak harus statis. Faktanya, karena topologi terkait dengan diversitas komunikasi partikel,[31] beberapa upaya telah dilakukan untuk membuat topologi adaptif (SPSO,[32] APSO,[33] stochastic star,[34] TRIBES,[35] Cyber Swarm,[36] dan C-PSO[37]) Dengan menggunakan topologi cincin, PSO dapat mencapai paralelisme tingkat generasi, yang secara signifikan meningkatkan kecepatan evolusi.[38] Proses kerjaAda beberapa aliran pemikiran tentang mengapa dan bagaimana algoritma PSO dapat melakukan optimasi. Keyakinan umum di antara para peneliti adalah bahwa perilaku kawanan bervariasi antara perilaku eksploratif, yaitu mencari wilayah yang lebih luas dari ruang pencarian, dan perilaku eksploitatif, yaitu pencarian yang berorientasi pada lokal sehingga lebih dekat ke optimal (mungkin lokal). Aliran pemikiran ini telah lazim sejak awal PSO.[3][4][12][16] Aliran pemikiran ini berpendapat bahwa algoritma PSO dan parameter-parameternya harus dipilih sedemikian rupa sehingga dapat menyeimbangkan dengan tepat antara eksplorasi dan eksploitasi untuk menghindari konvergensi dini ke suatu optimal lokal, tetapi tetap memastikan tingkat konvergen yang baik ke optimal. Keyakinan ini adalah pendahulu dari banyak varian PSO, lihat di bawah ini. Aliran pemikiran lainnya adalah bahwa perilaku kawanan PSO tidak dipahami dengan baik dalam hal bagaimana hal tersebut memengaruhi kinerja optimasi yang sebenarnya, terutama untuk ruang pencarian berdimensi lebih tinggi dan masalah optimasi yang mungkin diskontinyu, bising, dan bervariasi terhadap waktu. Aliran pemikiran ini hanya mencoba untuk menemukan algoritma dan parameter PSO yang menghasilkan kinerja yang baik terlepas dari bagaimana perilaku swarm dapat ditafsirkan dalam kaitannya dengan eksplorasi dan eksploitasi. Penelitian-penelitian tersebut telah menghasilkan penyederhanaan algoritma PSO, lihat di bawah. KonvergensiSehubungan dengan PSO, kata konvergensi biasanya mengacu pada dua definisi yang berbeda:
Konvergensi dari barisan solusi telah diteliti untuk PSO.[15][16][17] Analisis-analisis ini telah menghasilkan panduan untuk memilih parameter PSO yang diyakini dapat menyebabkan konvergensi pada suatu titik dan mencegah divergensi partikel kawanan (partikel-partikel tidak bergerak tanpa batas dan akan berkumpul di suatu tempat). Namun, analisis tersebut dikritik oleh Pedersen[22] karena terlalu menyederhanakan dengan mengasumsikan bahwa kawanan tersebut hanya memiliki satu partikel, tidak menggunakan variabel stokastik, dan titik-titik tariknya, yaitu posisi terbaik partikel p' dan posisi terbaik kawanan g', tetap konstan selama proses pengoptimalan. Namun, hal itu ditunjukkan[39] bahwa penyederhanaan ini tidak memengaruhi batas-batas yang ditemukan oleh penelitian-penelitian ini untuk parameter yang kawanan tersebut konvergen. Upaya yang cukup besar telah dilakukan dalam beberapa tahun terakhir untuk melemahkan asumsi pemodelan yang digunakan selama analisis stabilitas PSO,[40] dengan hasil umum terbaru yang berlaku untuk berbagai varian PSO dan memanfaatkan asumsi pemodelan minimal yang diperlukan.[41] Konvergensi ke optimum lokal telah dianalisis untuk PSO dalam [42] dan.[43] Telah terbukti bahwa PSO membutuhkan beberapa modifikasi untuk menjamin ditemukannya optimum lokal. Ini berarti bahwa menentukan kemampuan konvergensi dari algoritma dan parameter PSO yang berbeda masih bergantung pada hasil empiris. Salah satu upaya untuk mengatasi masalah ini adalah pengembangan strategi "pemelajaran ortogonal" untuk meningkatkan penggunaan informasi yang sudah ada dalam hubungan antara p' dan g', untuk membentuk contoh konvergen utama dan efektif dengan topologi PSO apa pun. Tujuannya adalah untuk meningkatkan kinerja PSO secara keseluruhan, termasuk konvergensi global yang lebih cepat, kualitas solusi yang lebih tinggi, dan robustness yang lebih kuat.[44] Namun, penelitian tersebut tidak memberikan bukti teoritis untuk membuktikan klaim mereka. Mekanisme adaptifTanpa memerlukan pertukaran antara konvergensi ('eksploitasi') dan divergensi ('eksplorasi'), sebuah mekanisme adaptif bisa diberlakukan. Adaptive particle swarm optimization (APSO) [45] memiliki efisiensi pencarian yang lebih baik daripada PSO standar. APSO dapat melakukan pencarian global di seluruh ruang pencarian dengan kecepatan konvergensi yang lebih tinggi. APSO memungkinkan kontrol otomatis terhadap bobot inersia, koefisien akselerasi, dan parameter algoritmik lainnya pada saat proses berjalan, sehingga meningkatkan efektivitas dan efisiensi pencarian secara bersamaan. Selain itu, APSO dapat mengambil tindakan terhadap partikel terbaik secara global untuk keluar dari kemungkinan optima lokal. Namun, APSO akan memperkenalkan parameter algoritma baru, tetapi tidak menambah kompleksitas desain atau implementasi. Selain itu, melalui pemanfaatan mekanisme evaluasi kecocokan (fitness) skala-adaptif, PSO dapat secara efisien mengatasi masalah optimasi yang mahal secara komputasi.[46] VarianBanyak variasi dari algoritma PSO, bahkan yang paling dasar sekalipun. Sebagai contoh, ada berbagai cara untuk menginisialisasi partikel dan kecepatan (misalnya, mulai dengan kecepatan nol), cara meredam kecepatan, hanya memperbarui pi dan g setelah seluruh kawanan telah diperbarui, dll. Beberapa pilihan ini dan dampak performa yang mungkin telah dibahas dalam literatur.[14] Sejumlah implementasi standar telah dibuat oleh peneliti terkemuka, "diciptakan untuk digunakan, baik sebagai dasar untuk pengujian performa perbaikan teknik PSO maupun untuk mewakili PSO kepada komunitas optimisasi yang lebih luas. Memiliki algoritma standar yang terkenal dan secara ketat didefinisikan memberikan titik perbandingan yang berharga yang dapat digunakan di seluruh bidang penelitian untuk menguji kemajuan baru dengan lebih baik."[10] Yang terbaru adalah Standard PSO 2011 (SPSO-2011).[47] HibridisasiVarian PSO yang baru dan lebih canggih juga terus diperkenalkan dalam upaya untuk meningkatkan kinerja optimasi. Ada beberapa tren dalam penelitian tersebut; salah satunya adalah membuat metode optimasi hibrida menggunakan PSO yang dikombinasikan dengan pengoptimal lain,[48][49][50] mis, menggabungkan PSO dengan optimasi berbasis biogeografi,[51] dan penggabungan metode pemelajaran yang efektif.[44] Mengatasi konvergensi prematurTren penelitian lain adalah mencoba dan mengatasi konvergensi prematur (yaitu, stagnasi optimasi), misalnya dengan membalikkan atau mengganggu pergerakan partikel PSO,[19][52][53][54] pendekatan lain untuk menangani konvergensi prematur adalah dengan menggunakan kawanan berganda[55] (multi-swarm optimization). Pendekatan multi-swarm juga dapat digunakan untuk mengimplementasikan optimasi multi-objektif.[56] Terakhir, ada perkembangan dalam mengadaptasi parameter perilaku PSO selama pengoptimalan.[45][24] PenyederhanaanAliran pemikiran lainnya adalah bahwa PSO harus disederhanakan sebanyak mungkin tanpa mengganggu kinerjanya; konsep umum yang sering disebut sebagai pisau cukur Occam. Penyederhanaan PSO pada awalnya disarankan oleh Kennedy[4] dan telah diteliti secara lebih ekstensif,[18][21][22][57] yang terlihat bahwa kinerja optimasi meningkat, dan parameter lebih mudah disetel serta berkinerja lebih konsisten di berbagai masalah optimasi. Argumen lain yang mendukung penyederhanaan PSO adalah bahwa metaheuristik hanya dapat dibuktikan kemanjurannya secara empiris dengan melakukan eksperimen komputasi dengan jumlah masalah optimasi yang terbatas. Ini berarti metaheuristik seperti PSO tidak dapat dibuktikan kebenarannya dan hal ini meningkatkan risiko terjadinya kesalahan dalam deskripsi dan implementasinya. Sebuah contoh yang baik dari hal ini [58] menyajikan varian yang menjanjikan dari algoritma genetika (metaheuristik populer lainnya), tetapi kemudian ditemukan cacat karena sangat bias dalam pencarian optimasi terhadap nilai yang sama untuk dimensi yang berbeda dalam ruang pencarian, yang kebetulan merupakan optimal dari masalah tolok ukur yang dipertimbangkan. Bias ini disebabkan oleh kesalahan pemrograman, dan sekarang telah diperbaiki.[59] Inisialisasi kecepatan mungkin memerlukan input tambahan. Varian Bare Bones PSO[60] telah diusulkan pada tahun 2003 oleh James Kennedy, dan sama sekali tidak perlu menggunakan kecepatan. Varian lain yang lebih sederhana adalah optimasi kawanan partikel yang diakselerasi (accelerated particle swarm optimization, APSO),[61] yang juga tidak perlu menggunakan velocity dan dapat mempercepat konvergensi di banyak aplikasi. Tersedia kode demo sederhana dari APSO.[62] Optimasi multi-objektifPSO juga telah diterapkan pada masalah multi-objektif,[63][64][65] yang mana perbandingan fungsi objektifnya mempertimbangkan dominansi Pareto ketika menggerakkan partikel PSO dan solusi yang tidak terdominasi disimpan untuk mendekati front pareto. Biner, diskrit, dan kombinatorialKarena persamaan PSO yang diberikan di atas bekerja pada bilangan riil, metode yang umum digunakan untuk menyelesaikan masalah diskrit adalah memetakan ruang pencarian diskrit ke domain kontinu, menerapkannya ke PSO klasik, dan kemudian memetakan hasilnya. Pemetaan seperti itu bisa sangat sederhana (misalnya dengan hanya menggunakan nilai pembulatan) atau lebih canggih.[66] Namun, perlu dicatat bahwa persamaan pergerakan menggunakan operator yang mengerjakan empat tindakan:
Biasanya posisi dan kecepatan diwakili oleh n bilangan riil, dan operator-operator ini adalah -, *, +, dan lagi +. Namun, semua objek matematika tersebut dapat didefinisikan dengan cara yang sama sekali berbeda, untuk menyelesaikan masalah biner (atau lebih umum lagi masalah diskrit), atau bahkan masalah kombinatorial.[67] [68][69][70] Salah satu pendekatannya adalah dengan mendefinisikan ulang operator-operator yang didasarkan pada himpunan.[71] Lihat juga
Referensi
Pranala eksternal
|
Portal di Ensiklopedia Dunia
![{\displaystyle [1,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0fcfee68a647afbfbe0440e15fc9fd260abbdc7)