左上:由螺旋带(又称瑞士卷 )中的1000个点组成的3维数据集,中间有矩形孔。右上:用于生成3维数据集的原始2维数据集。左下和右下:分别使用模块化数据处理(Modular Data Processing)工具箱实现的LLE(邻近线性嵌入)和黑塞LLE,对流形进行的2维复原。 非线性降维 也称作流形学习 ,为各种相关技术中的一种,是将高维数据投射到低维潜流形 上,目的是在低维空间中实现数据可视化,或学习映射(高维到低维嵌入或反之)本身。[ 1] [ 2] 降维 的线性分解法(如奇异值分解 、主成分分析 )。
考虑以矩阵(或数据库)表示的数据集,其中每行都代表描述某物特定实例的一组属性(或特征)。如果属性的数量很大,那么可行行空间 的增长速度是指数级的(例如有
f
{\displaystyle f}
k
{\displaystyle k}
k
f
{\displaystyle k^{f}}
人类往往难以理解高维数据。因此将数据减进行降维对于可视化非常有用。
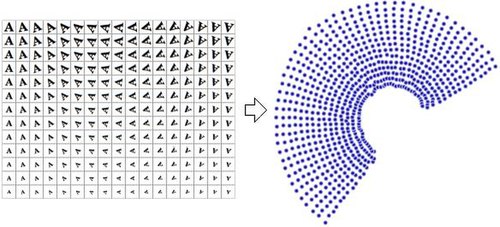
使用非线性降维算法(Manifold Sculpting)产生的二维(缩放和旋转)散点图。 数据的降维表示通常被称为“内蕴变量”(intrinsic variable),即它们是数据产生的价值。例如,考虑一个包含字母“A”经过缩放和旋转的图像的数据集,每张图片有32×32像素,可以表示为长度为1024的向量;每行都是1024维的空间(汉明空间
使用线性降维算法PCA产生的二维散点图,数据分布并不那么有条理 作为对比,右图使用线性降维算法PCA (主成分分析),将同样的数据集降为二维,可以发现结果并没有采用非线性降维算法好。这表明从该流形上采样得到的高维向量以一种非线性的方式变化。
非线性降维在计算机视觉领域有所应用。例如一个使用相机在封闭的静态环境中导航的机器人,相机得到的图像可以视为从高维空间流形采样得到的样本,流形的内蕴变量代表机器人的位置和朝向。
不变流形 对动力系统 中的模型降阶具有普遍意义。特别是,若相空间中存在吸引不变流形,附近的轨迹便会汇聚其上并停留,使其称为动力系统降维的候选流形。一般情形下不能保证存在这样的流形,不过谱子流形 理论给出了一大类动力系统中存在唯一吸引不变对象的条件。[ 3] [ 4]
下面列举了一些非线性降维技巧。
萨蒙映射
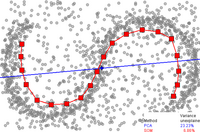
1维SOM的主曲线近似图(红色方格折线 ,20个节点)。第一主成分 表为蓝色直线。数据点为灰色圆圈。对PCA,此例中的未解释方差比 是23.23%,而SOM则是6.86%。[ 5]
自组织映射 (SOM,也称作科赫宁映射,Kohonen map)及其概率变体生成拓扑图 (GTM)使用嵌入空间中的点表示,根据从嵌入空间到高位空间的非线性映射形成潜变量模型 。[ 6]
核主成分分析 可能是应用最广泛的降维算法。[ 7]
m
×
n
{\displaystyle m\times n}
X
{\displaystyle \mathbf {X} }
C
=
1
m
∑
i
=
1
m
x
i
x
i
T
.
{\displaystyle C={\frac {1}{m}}\sum _{i=1}^{m}{\mathbf {x} _{i}\mathbf {x} _{i}^{\mathsf {T}}}.}
然后将数据投影到矩阵的前k 个特征向量上。相比之下,KPCA首先计算数据转换到高维空间后的协方差矩阵
C
=
1
m
∑
i
=
1
m
Φ
(
x
i
)
Φ
(
x
i
)
T
.
{\displaystyle C={\frac {1}{m}}\sum _{i=1}^{m}{\Phi (\mathbf {x} _{i})\Phi (\mathbf {x} _{i})^{\mathsf {T}}}.}
然后将变换后的数据投影到矩阵的前k 个特征向量上,这一步与PCA相同。它用核技巧 将大部分计算分解,这样整个过程就可在不实际计算
Φ
(
x
)
{\displaystyle \Phi (\mathbf {x} )}
Φ
{\displaystyle \Phi }
瑞士卷 流形上便表现不佳。不过,可构造与数据相关的核矩阵,将某些在此类环境中表现良好的其他方案(如拉普拉斯特征映射、LLE)视作核PCA的特例。[ 8]
主曲线的应用:生活质量指数。[ 9] 预期寿命 、婴儿死亡率 、结核病 发病率。不同样式与颜色对应不同的地理位置。红色粗线是主曲线 (principal curve),与数据集近似,用弹性映射 法绘制。[ 10] 主曲线与流形 给出了非线性降维的自然几何框架,并通过明确构建嵌入流形、使用流形上的标准几何投影进行编码,推广了PCA的几何解释。这种方法最早由Trevor Hastie (1984)提出,[ 11] [ 12] [ 13]
拉普拉斯特征映射用谱技术降维。[ 14] [ 15] 再生核希尔伯特空间 正则化的技术可以增加这种能力。[ 16]
主成分分析等传统技术不考虑数据的内蕴几何。拉普拉斯特征映射根据数据集的邻域信息构造了图,数据点是图中的节点,连通性取决于邻点的距离(如用k邻近算法 ),生成的图可视作低维流形在高位空间中的离散近似。基于图的代价函数最小化确保流形上相近的点映射到低维空间也相近,从而保留了局部距离。流形上拉普拉斯-贝尔特拉米算子 的特征函数可作为嵌入维度,因为在温和的条件下算子具有可数谱,是流形上平方可积函数的基础(与单位圆流形上的傅立叶级数 比较)。拉普拉斯特征映射的理论化取得了部分成功,因为在某些非限制性假设下,随着点数趋向无穷多,已经证明图拉普拉斯矩阵收敛到拉普拉斯-贝尔特拉米算子。[ 15]
等距特征映射 [ 17] Floyd-Warshall算法 与经典多维标度 (MDS)的结合。经典MDS采用所有点之间的成对距离矩阵,计算每个点的位置;等距特征映射假设只知道相邻点之间的成对距离,并用Floyd–Warshall算法计算其他点的距离,这样就能有效估算出所有点之间的成对测地距离 矩阵。然后等距特征映射用经典MDS计算所有点的降维位置。地标等距特征映射是这种算法的变体,用地标提高计算速度,但会牺牲一定精度。
流形学习中,输入数据被假定是从嵌入高维向量空间的低维流形中采样的。MVU背后的主要原理是利用流形的局部线性,在底流形的每点创建保留局部邻域的映射。
局部线性嵌入(LLE)与等距特征映射大约同时问世。[ 18] 系数矩阵 算法时优化速度更快、很多问题上的结果更好等等。LLE也始于寻找每个点的最近邻点,接着为每个点计算一组权重,其能将点描述为邻点的线性组合。最后用基于特征向量的优化技术,求得点的低维嵌入,这样每个点仍用邻点的相同线性组合描述。LLE处理非均匀样本密度时往往效果不佳,因为没有固定单位防止权重漂移。LLE没有内蕴模型。
LLE根据点
X
i
{\displaystyle X_{i}}
W
i
j
{\displaystyle W_{ij}}
E
(
W
)
{\displaystyle E(W)}
E
(
W
)
=
∑
i
|
X
i
−
∑
j
W
i
j
X
j
|
2
{\displaystyle E(W)=\sum _{i}\left|\mathbf {X} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {X} _{j}}\right|^{2}}
权重
W
i
j
{\displaystyle W_{ij}}
X
j
{\displaystyle X_{j}}
X
i
{\displaystyle X_{i}}
X
i
{\displaystyle X_{i}}
X
j
{\displaystyle X_{j}}
X
i
{\displaystyle X_{i}}
W
i
j
{\displaystyle W_{ij}}
∑
j
W
i
j
=
1
{\displaystyle \sum _{j}{\mathbf {W} _{ij}}=1}
原数据点是D 维空间中收集的,算法的目标是将维度降低到d 使
D
>>
d
{\displaystyle D>>d}
D 维空间构建第i 个数据点的权重
W
i
j
{\displaystyle W_{ij}}
d 维空间中构建同一点。基于这种想法,我们创建了一个保邻域映射:D 维空间中的每点
X
i
{\displaystyle X_{i}}
d 维空间中的某点
Y
i
{\displaystyle Y_{i}}
C
(
Y
)
=
∑
i
|
Y
i
−
∑
j
W
i
j
Y
j
|
2
{\displaystyle C(Y)=\sum _{i}\left|\mathbf {Y} _{i}-\sum _{j}{\mathbf {W} _{ij}\mathbf {Y} _{j}}\right|^{2}}
这个成本函数中,权重
W
i
j
{\displaystyle W_{ij}}
Y
i
{\displaystyle Y_{i}}
N 阶特征值问题 (N 为数据点数量)解决,其底部d 个非零特征向量提供了坐标的一组正交集。一般来说,数据点是根据欧氏距离测量的K 个最近邻点构建的,这时算法只有一个自由参数K ,可通过交叉验证来选择。
黑塞LLE也是基于稀疏矩阵技术,[ 19]
改进局部线性嵌入(MLLE)[ 20] 正交投影 。MLLE的创造者也是局部切空间对齐(LTSA)的作者,认识到每个权重向量的正交投影的全局优化本质上是对齐每个数据点的局部切空间时,LTSA就蕴含于MLLE的表述中。正确应用此算法的理论与经验意义深远。[ 21]
局部切空间对齐 (LTSA)[ 22] k 个最近邻域。通过计算每个局部邻域中的前d 个主成分,获得每个点的切空间。然后进行优化,找到能使切空间对齐的嵌入。
最大方差展开 、等距特征映射、LLE有共同的直觉:若流形被适当展开,则各点的方差会最大化。第一步是找到每个点的最近邻点;然后最大化所有非邻点间距离,约束是邻点间距不变。此算法的主要贡献在于将问题转化为半定规划问题。然而,半定规划求解器的计算成本很高。与LLE类似,最大方差展开没有内蕴模型。
自编码器 是一个前馈神经网络 ,其训练目标为恒等映射,即从向量映射到同一个向量。用于降维时,其部分隐藏层只包含少量神经元。此时,网络必须学会用较少的维度编码向量,并同时能将将其解码。因此,网络的前半部分(编码器,Encoder)从高维空间映射到低维空间,后半部分(解码器,Decoder)从低维空间映射到高维空间。自编码器的概念由来已久,[ 23] 受限玻尔兹曼机 和堆叠降噪自编码器成为可能。与自编码器相关的是NeuroScale算法,其使用多维标度 和萨蒙映射 学习高维空间到嵌入空间的非线性映射。mappings in NeuroScale中的映射基于径向基函数网络 。
高斯过程潜变量模型(GPLVM)[ 24] 高斯过程 形式)。不过,GPLVM中,映射是从嵌入(潜)空间到数据空间(如密度网络与GTM),而在核PCA中,映射方向正好相反。它最初是为高维空间的可视化提出的,但已被推广为构造两观测空间中间的共享流形模型。GPLVM及其许多变体都是专为人类运动建模而提出的,如后约束GPLVM、GP动态模型(GPDM)、平衡GPDM(B-GPDM)、拓扑约束GPDM等等。为在步态分析中捕捉姿态与步态流形的耦合效应,提出了多层步态-姿态联合流形。[ 25]
t分布随机邻域嵌入 (t-SNE)[ 26]
关系透视映射是一种多维标度 算法。算法通过模拟闭流形上的多粒子动态系统,在流形上找到数据点的构型,其中数据点被映射为粒子,间距(或差异)表为排斥力。随着流形逐渐增大,多粒子系统逐渐冷却,收敛到反映数据点距离信息的构型。
关系透视映射的灵感来自物理模型,当中带正电的粒子在球表面自由移动。在库仑力的引导下,粒子的最小能量构型将反映粒子间斥力的强度。
关系透视映射是1976年提出的。[ 27] 环面 作为像流形,后来VisuMap 软件中进行了扩展,使用球面 、射影空间 、克莱因瓶 等其他闭流形作为像流形。
传播图使用网络上的多个传播源,将节点映射为点云。[ 28] 全局级联模型 中,传播速度可通过阈值参数
t
∈
[
0
,
1
]
{\displaystyle t\in [0,1]}
t
=
0
{\displaystyle t=0}
等距特征映射 算法。
曲线成分分析(CCA)在输出空间中寻找点的构型,尽可能保留原始距离,并关注输出空间中的小距离(与萨蒙映射 相反,后者关注原空间的小距离)[ 29]
注意CCA作为一种迭代学习算法,实际上是先关注大距离(与萨蒙映射类似),逐渐转向小距离。若要在两者间做出妥协,小距离信息将覆盖大距离信息。
CCA的压力函数与右Bregman散度之和有关。[ 30]
CDA[ 29]
微分同胚 降维或Diffeomap [ 31]
流形对齐 利用的假设是:相似过程产生的数据集将共享相似的底流形表示。学习从原空间到共享流形的投影,可以恢复对应关系,并可将知识在领域间转移。大多数流形对齐技术只考虑两个数据集,不过遮盖奶奶可推广到任意多的初数据集。[ 32]
扩散映射 利用热扩散 与随机游走 (马尔可夫链 )之间的关系;流形上的扩散算子类似于对图上的函数进行操作的马尔可夫转移矩阵,图的节点从流形中采样而来。[ 33]
X
=
[
x
1
,
x
2
,
…
,
x
n
]
∈
Ω
⊂
R
D
{\displaystyle \mathbf {X} =[x_{1},x_{2},\ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}} }
d
{\displaystyle \mathbf {d} }
X 表示数据集,
μ
{\displaystyle \mu }
X 上的数据点分布,定义核 代表X 中点的某种相似性(affinity)。核
k
{\displaystyle {\mathit {k}}}
[ 34]
k
(
x
,
y
)
=
k
(
y
,
x
)
,
{\displaystyle k(x,y)=k(y,x),}
k 对称
k
(
x
,
y
)
≥
0
∀
x
,
y
,
k
{\displaystyle k(x,y)\geq 0\qquad \forall x,y,k}
k 是保正的
因此可将单个数据点视作图的节点,核k 则定义了图上的某种亲和性(affinity)。由于核对称,图在构造上也是对称的。从这里不难看出,通过元组
(
X
,
k
)
{\displaystyle (\mathbf {X} ,\ \mathbf {k} )}
马尔可夫链 。这种技术在很多领域都有应用,称作图拉普拉斯(graph Laplacian)。
例如,图
K
=
(
X
,
E
)
{\displaystyle \mathbf {K} =(X,\ E)}
K
i
j
=
{
e
−
‖
x
i
−
x
j
‖
2
2
/
σ
2
if
x
i
∼
x
j
0
otherwise
{\displaystyle K_{ij}={\begin{cases}e^{-\|x_{i}-x_{j}\|_{2}^{2}/\sigma ^{2}}&{\text{if }}x_{i}\sim x_{j}\\0&{\text{otherwise}}\end{cases}}}
上式中,
x
i
∼
x
j
{\displaystyle x_{i}\sim x_{j}}
x
i
{\displaystyle x_{i}}
x
j
{\displaystyle x_{j}}
测地 距离应用来实际测量流形 上的距离。由于不能获得流形的精确结构,对于最近邻点,测地距可用欧氏距离近似表示。
σ
{\displaystyle \sigma }
‖
x
i
−
x
j
‖
2
≫
σ
{\displaystyle \|x_{i}-x_{j}\|_{2}\gg \sigma }
K
i
j
=
0
{\displaystyle K_{ij}=0}
‖
x
i
−
x
j
‖
2
≪
σ
{\displaystyle \|x_{i}-x_{j}\|_{2}\ll \sigma }
K
i
j
=
1
{\displaystyle K_{ij}=1}
σ
{\displaystyle \sigma }
[ 35]
要忠实表示马尔可夫矩阵,K 必须被相应的度数矩阵 D 归一化:
P
=
D
−
1
K
.
{\displaystyle P=D^{-1}K.}
现在P 表示马尔可夫链。
P
(
x
i
,
x
j
)
{\displaystyle P(x_{i},x_{j})}
x
i
{\displaystyle x_{i}}
x
j
{\displaystyle x_{j}}
t 时间步内从
x
i
{\displaystyle x_{i}}
x
j
{\displaystyle x_{j}}
P
t
(
x
i
,
x
j
)
{\displaystyle P^{t}(x_{i},x_{j})}
P
t
{\displaystyle P^{t}}
P 的t 次幂。
马尔可夫矩阵P 构成了数据集X 的某种局部集合概念。扩散映射与主成分分析 的主要区别在于,前者只考虑数据的局部特征,而不考虑整个数据集的相关性。
K 定义了数据集上的随机游走,这是说核捕捉到了数据集的某些局部几何特征。马尔可夫链定义了通过核值传播的快慢方向:游走在时间上向前传播时,局部几何信息会以与动力系统的局部变换(由微分方程定义)相同的方式聚集起来。[ 34]
{
D
t
}
t
∈
N
{\displaystyle \{D_{t}\}_{t\in N}}
D
t
2
(
x
,
y
)
=
‖
p
t
(
x
,
⋅
)
−
p
t
(
y
,
⋅
)
‖
2
{\displaystyle D_{t}^{2}(x,y)=\|p_{t}(x,\cdot )-p_{t}(y,\cdot )\|^{2}}
对固定的t值,
D
t
{\displaystyle D_{t}}
x 和y 间相连的路径越多,
D
t
(
x
,
y
)
{\displaystyle D_{t}(x,y)}
D
t
(
x
,
y
)
{\displaystyle D_{t}(x,y)}
t 的所有路径综合,因此
D
t
{\displaystyle D_{t}}
D
t
{\displaystyle D_{t}}
x 、y 点之间的所有关系,是比欧氏距离、甚至测地距离更好的邻近度概念。
局部多维标度在局部进行多维标度 ,再用凸优化将所有小块拼接在一起。[ 36]
非线性PCA(NLPCA)用反向传播算法 训练多层感知机(MLP),使其与流形相匹配。[ 37]
数据驱动的高维缩放(DD-HDS)[ 38] 萨蒙映射 与曲线成分分析密切相关,不同之处在于:(1) DD-HDS会关注原空间与输出空间中的小距离,同时惩罚假邻域与撕裂;(2) DD-HDS通过距离分布调整权函数,以考虑度量集中 现象。
流形雕刻(manifold sculpting)[ 39] 分级优化 寻找嵌入。与其他算法类似,它也会计算k 个最近邻点,并试图求出能保留局部邻域关系的嵌入。流形雕刻可以缓慢地将方差从高维缩放出来,同时调整低维的点,以保留其关系。若缩放率很小,则就能找到很精确的嵌入。流形雕刻与其他算法相比,在解决部分问题时表现出更高的经验精度,还可完善其他流形学习算法的结果。不过,除非哦用非常慢的缩放速率,否则展开某些流形时会非常吃力。流形雕刻没有内蕴模型。
RankVisu
RankVisu[ 40]
拓扑约束等距嵌(TCIE)[ 41] 压力最大化 中基于较小的权重。
均匀流形近似与投影(UMAP)[ 42] 局部连通 的黎曼流形 上,且黎曼度量 是局部常或近似局部常的。[ 43]
基于近似矩阵的方法是指数据以相似性矩阵 或距离矩阵 的形式呈现给算法。这些方法都属于度量多维缩放(metric multidimensional scaling),主要差别在于如何计算近似,如等距特征映射 、局部线性嵌入 、最大方差展开 、萨蒙映射 (实际上不是映射)等等,都属于度量多维缩放。
^ Lawrence, Neil D. A unifying probabilistic perspective for spectral dimensionality reduction: insights and new models . Journal of Machine Learning Research . 2012, 13 (May): 1609–38. Bibcode:2010arXiv1010.4830L arXiv:1010.4830 ^ Lee, John A.; Verleysen, Michel. Nonlinear Dimensionality Reduction . Springer. 2007. ISBN 978-0-387-39350-6 ^ Haller, George; Ponsioen, Sten. Nonlinear normal modes and spectral submanifolds: Existence, uniqueness and use in model reduction. Nonlinear Dynamics. 2016, 86 (3): 1493–1534. S2CID 44074026 arXiv:1602.00560 doi:10.1007/s11071-016-2974-z ^ Gashler, M.; Martinez, T. Temporal Nonlinear Dimensionality Reduction (PDF) . Proceedings of the International Joint Conference on Neural Networks IJCNN'11: 1959–66. 2011. ^ The illustration is prepared using free software: Mirkes, E.M. Principal Component Analysis and Self-Organizing Maps: applet . University of Leicester. 2011.
^ Yin, Hujun. 3. Learning Nonlinear Principal Manifolds by Self-Organising Maps . Gorban, A.N.; Kégl, B.; Wunsch, D.C.; Zinovyev, A. (编). Principal Manifolds for Data Visualization and Dimension Reduction. Lecture Notes in Computer Science and Engineering 58 . Springer. 2007: 68–95. ISBN 978-3-540-73749-0 ^ Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural Computation (MIT Press ). 1998, 10 (5): 1299–1319. S2CID 6674407 doi:10.1162/089976698300017467 ^ Ham, Jihun; Lee, Daniel D.; Mika, Sebastian; Schölkopf, Bernhard. A kernel view of the dimensionality reduction of manifolds. Proceedings of the 21st International Conference on Machine Learning, Banff, Canada, 2004. doi:10.1145/1015330.1015417 ^ Gorban, A. N.; Zinovyev, A. Principal manifolds and graphs in practice: from molecular biology to dynamical systems. International Journal of Neural Systems . 2010, 20 (3): 219–232. PMID 20556849 S2CID 2170982 arXiv:1001.1122 doi:10.1142/S0129065710002383 ^ A. Zinovyev, ViDaExpert - Multidimensional Data Visualization Tool Institut Curie , Paris.
^ Hastie, T. Principal Curves and Surfaces (PDF) (学位论文). Stanford Linear Accelerator Center, Stanford University. November 1984. (原始内容存档 (PDF) 于2019-08-02). ^ Hastie, T. ; Stuetzle, W. Principal Curves (PDF) . Journal of the American Statistical Association . June 1989, 84 (406): 502–6. doi:10.1080/01621459.1989.10478797 ^ Gorban, A. N. ; Kégl, B.; Wunsch, D. C.; Zinovyev, A. (编). Principal Manifolds for Data Visualisation and Dimension Reduction . Lecture Notes in Computer Science and Engineering (LNCSE) 58 . Springer. 2007. ISBN 978-3-540-73749-0 ^ Belkin, Mikhail; Niyogi, Partha . Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering (PDF) . Advances in Neural Information Processing Systems (MIT Press). 2001, 14 : 586–691. ISBN 0-262-27173-7OCLC 52710683 ^ 15.0 15.1 Belkin, Mikhail. Problems of Learning on Manifolds (学位论文). Department of Mathematics, The University of Chicago. August 2003. Ohio-state.edu ^ Bengio, Yoshua; Paiement, Jean-Francois; Vincent, Pascal; Delalleau, Olivier; Le Roux, Nicolas; Ouimet, Marie. Out-of-Sample Extensions for LLE, Isomap, MDS, Eigenmaps, and Spectral Clustering (PDF) . Advances in Neural Information Processing Systems 16 . MIT Press. 2004. ISBN 0-262-20152-6 ^ Tenenbaum, J B.; de Silva, V.; Langford, J.C. A Global Geometric Framework for Nonlinear Dimensionality Reduction (PDF) . Science. 2000, 290 (5500): 2319–23. Bibcode:2000Sci...290.2319T PMID 11125149 S2CID 221338160 doi:10.1126/science.290.5500.2319 ^ Roweis, S. T.; Saul, L. K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science. 2000, 290 (5500): 2323–6. Bibcode:2000Sci...290.2323R PMID 11125150 S2CID 5987139 doi:10.1126/science.290.5500.2323 ^ Donoho, D.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data . Proc Natl Acad Sci U S A. 2003, 100 (10): 5591–6. Bibcode:2003PNAS..100.5591D PMC 156245 PMID 16576753 doi:10.1073/pnas.1031596100 ^ Zhang, Z.; Wang, J. MLLE: Modified Locally Linear Embedding Using Multiple Weights . NIPS'06: Proceedings of the 19th International Conference on Neural Information Processing Systems. 2006: 1593–1600. ^ Sidhu, Gagan. Locally Linear Embedding and fMRI feature selection in psychiatric classification . IEEE Journal of Translational Engineering in Health and Medicine. 2019, 7 : 1–11. PMC 6726465 PMID 31497410 S2CID 201832756 arXiv:1908.06319 doi:10.1109/JTEHM.2019.2936348 ^ Zhang, Zhenyue; Hongyuan Zha. Principal Manifolds and Nonlinear Dimension Reduction via Local Tangent Space Alignment. SIAM Journal on Scientific Computing. 2005, 26 (1): 313–338. CiteSeerX 10.1.1.211.9957 doi:10.1137/s1064827502419154 ^ DeMers, D.; Cottrell, G.W. Non-linear dimensionality reduction. Advances in neural information processing systems 5 . 1993: 580–7. ISBN 1558600159OCLC 928936290 ^ Lawrence, N. Probabilistic Non-linear Principal Component Analysis with Gaussian Process Latent Variable Models . Journal of Machine Learning Research. 2005, 6 : 1783–1816. ^ Ding, M.; Fan, G. Multilayer Joint Gait-Pose Manifolds for Human Gait Motion Modeling . IEEE Transactions on Cybernetics. 2015, 45 (11): 2413–24. PMID 25532201 S2CID 15591304 doi:10.1109/TCYB.2014.2373393 ^ van der Maaten, L.J.P.; Hinton, G.E. Visualizing High-Dimensional Data Using t-SNE (PDF) . Journal of Machine Learning Research. 2008, 9 : 2579–2605. ^ Li, James X. Visualizing high-dimensional data with relational perspective map (PDF) . Information Visualization. 2004, 3 : 49–59. S2CID 7566939 doi:10.1057/palgrave.ivs.9500051 ^ Taylor, D.; Klimm, F.; Harrington, H. A.; Kramár, M.; Mischaikow, K.; Porter, M. A.; Mucha, P. J. Topological data analysis of contagion maps for examining spreading processes on networks . Nature Communications. 2015, 6 : 7723. Bibcode:2015NatCo...6.7723T PMC 4566922 PMID 26194875 arXiv:1408.1168 doi:10.1038/ncomms8723 ^ 29.0 29.1 Demartines, P.; Hérault, J. Curvilinear Component Analysis: A Self-Organizing Neural Network for Nonlinear Mapping of Data Sets (PDF) . IEEE Transactions on Neural Networks. 1997, 8 (1): 148–154. PMID 18255618 doi:10.1109/72.554199 ^ Sun, Jigang; Crowe, Malcolm; Fyfe, Colin. Curvilinear component analysis and Bregman divergences (PDF) . European Symposium on Artificial Neural Networks (Esann). d-side publications. 2010: 81–86. ^ Walder, Christian; Schölkopf, Bernhard. Diffeomorphic Dimensionality Reduction (PDF) . Advances in Neural Information Processing Systems 22 . MIT Press. 2009: 1713–20. ^ Wang, Chang; Mahadevan, Sridhar. Manifold Alignment using Procrustes Analysis (PDF) . The 25th International Conference on Machine Learning: 1120–7. July 2008. ^ Lafon, Stephane. Diffusion Maps and Geometric Harmonics (学位论文). Yale University . May 2004. ^ 34.0 34.1 Coifman, Ronald R.; Lafon, Stephane. Diffusion Maps (PDF) . Applied and Computational Harmonic Analysis. July 2006, 21 (1): 5–30. S2CID 17160669 doi:10.1016/j.acha.2006.04.006 ^ Bah, B. Diffusion Maps: Applications and Analysis (学位论文). University of Oxford. 2008. ^ Venna, J.; Kaski, S. Local multidimensional scaling. Neural Networks. 2006, 19 (6–7): 889–899. PMID 16787737 doi:10.1016/j.neunet.2006.05.014 ^ Scholz, M.; Kaplan, F.; Guy, C. L.; Kopka, J.; Selbig, J. Non-linear PCA: a missing data approach. Bioinformatics (Oxford University Press). 2005, 21 (20): 3887–95. PMID 16109748 doi:10.1093/bioinformatics/bti634 hdl:11858/00-001M-0000-0014-2B1F-2 ^ S. Lespinats, M. Verleysen, A. Giron, B. Fertil, DD-HDS: a tool for visualization and exploration of high-dimensional data, IEEE Transactions on Neural Networks 18 (5) (2007) 1265–1279.
^ Gashler, M. and Ventura, D. and Martinez, T., Iterative Non-linear Dimensionality Reduction with Manifold Sculpting
^ Lespinats S., Fertil B., Villemain P. and Herault J., Rankvisu: Mapping from the neighbourhood network , Neurocomputing, vol. 72 (13–15), pp. 2964–2978, 2009.
^ Rosman, G.; Bronstein, M.M.; Bronstein, A.M.; Kimmel, R. Nonlinear Dimensionality Reduction by Topologically Constrained Isometric Embedding (PDF) . International Journal of Computer Vision. 2010, 89 (1): 56–68. S2CID 1365750 doi:10.1007/s11263-010-0322-1 ^ McInnes, Leland; Healy, John; Melville, James. Uniform manifold approximation and projection for dimension reduction. 2018-12-07. arXiv:1802.03426 ^ UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction — umap 0.3 documentation . umap-learn.readthedocs.io. [2019-05-04 ] . ^ ELastic MAPs . [2016-05-30 ] . (原始内容 存档于2011-07-20).





















![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)

![{\displaystyle \mathbf {X} =[x_{1},x_{2},\ldots ,x_{n}]\in \Omega \subset \mathbf {R^{D}} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/27767b00cc5714632b393ff3d9173e6eece42867)























