雙四角錐 |
| 類別 | 雙錐體 |
|---|
| 對偶多面體 | 四角柱 |
|---|
|
考克斯特符號
|     
     |
|---|
| 施萊夫利符號 | { }+{4} |
|---|
| 康威表示法 | dP4 |
|---|
|
| 面 | 8 |
|---|
| 邊 | 12 |
|---|
| 頂點 | 6 |
|---|
| 歐拉特徵數 | F=8, E=12, V=6 (χ=2) |
|---|
|
| 面的種類 | 8個三角形(側面)
基底為四邊形 |
|---|
面的佈局
| V4.4.4 |
|---|
|
| 對稱群 | D4h, [4,2], (*224), order 16 |
|---|
旋轉對稱群
| D4, [4,2]+, (224), order 8 |
|---|
|
| 凸 |
|
|
|
|
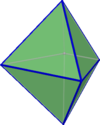
在幾何學中,雙四角錐是指以四邊形做為基底的雙錐體,由於雙錐體是由二個錐體疊起來的,因此不存在底面,因此只能討論其基底之形狀。當基底的形狀為正方形時會成為雙正四角錐又稱為正四角雙錐。若基底的形狀為正方形且每個面皆為正三角形則為正八面體。所有四角柱都有8個面6個頂點和12個邊。對偶多面體是四角柱。

只要基底是四邊形皆稱為雙四角錐
|
正四角雙錐
基底為正方形和且每一個面皆為正三角形的雙錐體稱為正四角雙錐,即是正八面體,是柏拉圖立體之一。

正四角雙錐
|
長方雙錐
基底為長方形的雙四角錐稱為長方雙錐。

長方雙錐
|
梯形雙錐
基底是梯形的雙四角錐稱為梯形雙錐
梯形雙錐
|
凹雙四角錐
 底面為凹鷂形的雙四角錐
底面為凹鷂形的雙四角錐
凹雙四角錐是指有一個角大於180度的雙四角錐,通常凹雙四角錐都是因為基底為凹四邊形才會構成
相關多面體與鑲嵌
半正方形二面體球面多面體
| 對稱群:[4,2], (*422)
|
[4,2]+, (422)
|
[1+,4,2], (222)
|
[4,2+], (2*2)
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|

|

|

|
| {4,2}
|
t{4,2}
|
r{4,2}
|
2t{4,2}=t{2,4}
|
2r{4,2}={2,4}
|
rr{4,2}
|
tr{4,2}
|
sr{4,2}
|
h{4,2}
|
s{2,4}
|
| 半正對偶
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|
    
|

|

|

|

|

|

|

|

|

|

|
| V42
|
V82
|
V42
|
V4.4.4
|
V24
|
V4.4.4
|
V4.4.8
|
V3.3.3.4
|
V22
|
V3.3.2.3
|
參見
































