正七角反棱柱 類別 反棱柱 柱狀均勻多面體 對偶多面體 七方偏方面體 名稱 正七角反棱柱 參考索引 U 77(e) 鮑爾斯縮寫 heap 考克斯特符號 施萊夫利符號 sr{2,7} 威佐夫符號 | 2 2 7 康威表示法 A7 面 16 邊 28 頂點 14 歐拉特徵數 F=16, E=28, V=14 (χ=2) 面的種類 14個三角形 正七邊形 面的佈局 14{3}+2{7} 頂點圖 3.3.3.7 對稱群 D7d , [2+ ,14], (2*7), order 28旋轉對稱群 D7 , [7,2]+ , (722), order 14 凸
在幾何學中,七角反棱柱 又稱為反七角柱 或七角反柱 是指底為七邊形 的反棱柱 ,側面由三角形 組成,若每一個面皆為正多邊形則稱為正七角反棱柱 。每個七角反棱柱皆含有16個面[ 1] [ 2] [ 3] 十六面體 。
正七角反棱柱 是基底為正七邊形 的七角反棱柱,其可視為一種半正多面體,施萊夫利符號 s{2,7}表示其可以藉由七邊形二面體透過扭稜變換構造。其具有D7 對稱群[ 4] 威佐夫符號 [ 5]
當底面為正七邊形時,會具備一些特別的性質
當基底邊長為a的時候:
高:
1
2
a
4
−
sec
π
14
sec
π
14
{\displaystyle {\frac {1}{2}}a{\sqrt {4-\sec {\frac {\pi }{14}}\sec {\frac {\pi }{14}}}}}
7
2
a
2
(
cot
π
7
+
3
)
{\displaystyle {\frac {7}{2}}a^{2}(\cot {\frac {\pi }{7}}+{\sqrt {3}})}
7
12
a
3
(
cot
π
14
+
cot
π
7
)
1
−
1
4
sec
π
14
sec
π
14
{\displaystyle {\frac {7}{12}}a^{3}(\cot {\frac {\pi }{14}}+\cot {\frac {\pi }{7}}){\sqrt {1-{\frac {1}{4}}\sec {\frac {\pi }{14}}\sec {\frac {\pi }{14}}}}}
半正七邊形二面體球面多面體
對稱群 [7,2] , (*722)
[7,2]+ , (722)
{7,2} t{7,2} r{7,2} 2t{7,2}=t{2,7}
2r{7,2}={2,7} rr{7,2} tr{7,2} sr{7,2}
半正對偶
V72 V142 V72 V4.4.7
V27 V4.4.7
V4.4.14 V3.3.3.7
半正反棱柱系列
2
3
4
5
6
7
8
9
10
11
12
n
s{2,4}
s{2,6}
s{2,8}
s{2,10}
s{2,12}
s{2,14}
s{2,16}
s{2,18}
s{2,20}
s{2,22}
s{2,24}
s{2,2n }
作為球面鑲嵌
^ Pugh, Anthony, Polyhedra: A Visual Approach , University of California Press: 21, 27, 62, 1976 [2014-06-22 ] , ISBN 9780520030565存档 于2014-07-09) ^ heptagonal antiprism vertices (页面存档备份 ,存于互联网档案馆 ) wolframalpha.com [2014-06-22]^ net of heptagonal antiprism (页面存档备份 ,存于互联网档案馆 ) korthalsaltes.com [2014-06-22]^ Melnyk, Theodor William, Osvald Knop, and William Robert Smith. "Extremal arrangements of points and unit charges on a sphere: equilibrium configurations revisited." Canadian Journal of Chemistry 55.10 (1977): 1745-1761.
^ Heptagonal prisms and antiprisms (页面存档备份 ,存于互联网档案馆 ) umanitoba.ca [2014-6-22]^ {7}-antiprism (页面存档备份 ,存于互联网档案馆 ) antiprism.com [2014-6-22]^ Heptagonal Antiprism (页面存档备份 ,存于互联网档案馆 ) dmccooey.com [2014-6-22]
Fowler, P. W., T. Tarnai, and Zs Gáspár. "From circle packing to covering on a sphere with antipodal constraints." Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 458.2025 (2002): 2275-2287.
heptagonal antiprism (页面存档备份 ,存于互联网档案馆 ) rediff.com [2014-6-22]
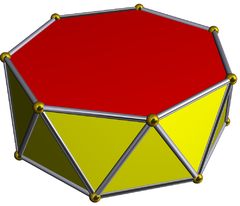


![正七角反棱柱[6]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/2e/Antiprism_7.png/120px-Antiprism_7.png)












