函數基於色相環複變函數圖形的資料視覺化
函數基於色相環複變函數圖形的資料視覺化
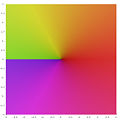
 高斯平面上對應複數的色相環複變著色,上色方式是依據文字描述的第一種定義:零是黑色、-1為紅色、1是青色、無限大為白色
高斯平面上對應複數的色相環複變著色,上色方式是依據文字描述的第一種定義:零是黑色、-1為紅色、1是青色、無限大為白色
色相環複變函數圖形是一種複變函數圖形的呈現方式,是一種飽和度固定為最飽和,將色相表示函數值的輻角、明度表示函數值的絕對值來表達複變函數的定義域著色方法[1],這種方法又稱為色相環法(color wheel method)[2]。
歷史
使用色相環法的定義域著色早在1980年代末就已被拉里·柯榮(英語:Larry Crone)和漢斯·隆達馬克(Hans Lundmark)首先使用。但與之相關的其他的複變函數繪圖直到1998年左右時由法蘭克·菲莉絲(英語:Frank Farris)統整併統稱為定義域著色[3]。
方法
 函數
函數 的在第二種定義下的色相環複變函數圖形。 黑色區塊有較大的絕對值。這個函數在
的在第二種定義下的色相環複變函數圖形。 黑色區塊有較大的絕對值。這個函數在 時存在本质奇点。
時存在本质奇点。
 對數函數在第三種定義的圖像。
對數函數在第三種定義的圖像。
這種函數圖形表示方有有兩種:

- 另一種原點是白色、1為紅色、-1是青色、無限大為黑色:

- 另外也有類似第一種的上色方式:原點是黑色、1為紅色、-1是青色、無限大為白色:

更確切地說,複數的輻角(角度)以色相來表示,而模量(絕對值)以HLS色彩模型(色調、亮度、飽和度)中的亮度來表示;對於給定的(H, L)數對,在這個模型中選擇最大飽和度值來呈現指定的複數。這幾種上色方式,最鮮豔的顏色以旋轉的方式出現在複數高斯平面的單位圓上,根據面兩種定義,1的六個六次方根(從1開始、逆時針)顏色分別為紅色、黃色、綠色、青藍、藍色和洋紅。此外,在這種配置上,兩個非常接近的複數其亮度值也會非常接近,若其輻角相同,則絕對值較大者,根據第一和最後一種定義,其顏色會較淺;根據第二種定義,其顏色會較深,反之亦然。
然而,HSL色彩空間在視覺上並不均勻,而導致在黃色、青色和品紅色表達的複數出現亮度差異的條紋,即使其絕對值與紅色、綠色和藍色相同條紋仍明顯可見,在單位圓上( )附近也可以見到一圈明顯的暈圈。Lab等色彩空間更加接近人類感知,可以校正HSL的不均勻問題,使圖像視覺上更準確、更加柔和[註 1]。
)附近也可以見到一圈明顯的暈圈。Lab等色彩空間更加接近人類感知,可以校正HSL的不均勻問題,使圖像視覺上更準確、更加柔和[註 1]。
針對色相環複變函數圖形,為了使圖像具可比較性,數學函數數位圖書館(The Digital Library of Mathematical Functions, DLMF)對此定義了一套標準的色彩配置方式[4]。
複數色彩空間
複數色彩空間是這種定義域著色方法的色彩空間,每個複數皆有對應唯一一種顏色,但是由於其定義上飽和度為定值,因此在這個色彩空間中並非所有色彩都能對應到一個複數。但這種色彩空間和HSL色彩空間一樣在視覺上有不均勻的缺點,因此數位圖書館有一套將標準色相環進行微調,其將單位為弧度的色相值以 映射到q,然後以公式換算[4]:
映射到q,然後以公式換算[4]:

其他上色方式
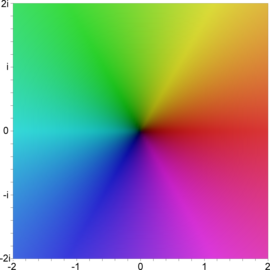 高斯平面上對應複數的色相環在此種定義下的複變著色,實部與虛部範圍皆為-2到2。
高斯平面上對應複數的色相環在此種定義下的複變著色,實部與虛部範圍皆為-2到2。
亦有另外一種依據色相上色的定義域著色方法,其依據HSV上色,但是飽和度不取定值,明度與飽和度取決於絕對值的對數值,在表達複數上比前者僅用亮度變化表示複數的方式能得到更多反差,但由於仍屬於色相環色彩空間,因此仍有視覺不平均問題。
以絕對值的明度或亮度以對數或指數倒數來表示複變函數圖形分別有不同的用途,例如對數成長較慢,因此當值域數字差異很大時適合使用絕對值以對數值來上色的版本,而指數倒數則適用於值域數字相當小的複變函數,例如絕對值在零與一之間震盪的函數。
這種明度與飽和度取決於絕對值的對數值一般會定義為[5]:




其中r為絕對值取對數的結果,a、b、c是調整結果用的係數。
-

-
-
-
-
-
-

-

參見
註解
參考文獻
外部連結