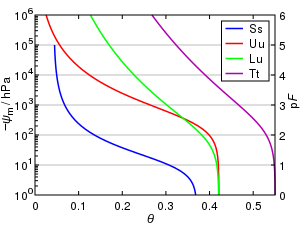
砂土、粘壤土、黏土和泥煤的水分持留曲线。 水分持留曲线 描述土壤含水量 θ和土壤水势 ψ之间的关系。不同类型土壤的水分持留曲线都是特异的,因此该曲线也被叫做土壤水分特征曲线 。
该曲线常被用来估计土壤蓄水量、对植物的供水能力(田间持水量 )以及土壤团聚体稳定性。由于水进入和离开土壤孔隙具有迟滞 效应,润湿和干燥曲线也可以区分开。
水分持留曲线的总体特征如图所示,该图横纵坐标分别为体积含水量θ和基质势
Ψ
m
{\displaystyle \Psi _{m}}
凋萎点
砂土中的水主要是靠毛细作用来吸收的,因此在较高(较小绝对值)势能下,大部分水会流失。然而黏土由于粘附和渗透的存在,会在较低势能下才释放水分。在任意势能下,泥煤土的水含量通常比黏土要高,而后者的含水量一般比砂土高。任意土壤的持水性都和土壤孔隙度以及土壤结合力的特性有关。
有多种模型可以用来描述水分持留曲线的形状,其中一种是van Genuchten模型:[ 1]
θ
(
ψ
)
=
θ
r
+
θ
s
−
θ
r
[
1
+
(
α
|
ψ
|
)
n
]
1
−
1
/
n
{\displaystyle \theta (\psi )=\theta _{r}+{\frac {\theta _{s}-\theta _{r}}{\left[1+(\alpha |\psi |)^{n}\right]^{1-1/n}}}}
其中
θ
(
ψ
)
{\displaystyle \theta (\psi )}
3 L−3 ];
|
ψ
|
{\displaystyle |\psi |}
θ
s
{\displaystyle \theta _{s}}
3 L−3 ];
θ
r
{\displaystyle \theta _{r}}
3 L−3 ];
α
{\displaystyle \alpha }
α
>
0
{\displaystyle \alpha >0}
−1 ], or cm−1 );
n
{\displaystyle n}
n
>
1
{\displaystyle n>1}
基于上述参数化方式,我们构建了一个能够对不饱和导水率-饱和-压力关系作出预测的模型。[ 2]
1907年,物理学家埃德加·白金漢姆 [ 2]
范格魯切騰(Van Genuchten)参数(
α
{\displaystyle \alpha }
n
{\displaystyle n}
[ 3]
ψ
{\displaystyle \psi }
含水量
θ
{\displaystyle \theta }
S
e
{\displaystyle Se}
最小二乘 法等数学技巧能够用来解出范格魯切騰参数。[ 4]
θ
{\displaystyle \theta }
ψ
{\displaystyle \psi }
^ van Genuchten, M.Th. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils (PDF) . Soil Science Society of America Journal. 1980, 44 (5): 892–898 [2016-11-01 ] . doi:10.2136/sssaj1980.03615995004400050002x 原始内容 (PDF) 存档于2013-06-18). ^ 2.0 2.1 Buckingham, Edgar, Studies on the movement of soil moisture , Bureau of Soils, Bulletin 38 , Washington, D.C.: U.S. Department of Agriculture, 1907 ^ Watson, K.K.. An instantaneous profile method for determining the hydraulic conductivity of unsaturated porous materials. Water Resources Research. 1966, 2 (4): 709–715. Bibcode:1966WRR.....2..709W doi:10.1029/WR002i004p00709 ^ Chou, T.K. A free GUI application for solving the van Genuchten parameters using non-linear least-squares minimization and curve-fitting (PDF) . www.cmcsjc.com. 2016,. January: 1–5. (原始内容 (PDF) 存档于2016-03-04).

![{\displaystyle \theta (\psi )=\theta _{r}+{\frac {\theta _{s}-\theta _{r}}{\left[1+(\alpha |\psi |)^{n}\right]^{1-1/n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/215d9c2dda9d084a016a5a86296300f917923472)










