这幅图展示了一个在三尖瓣线 的内部旋转的转针。 在它转动的每一阶段(除了一个端点是在三尖瓣线的一个顶点时),转针与三尖瓣线相交于三个点:两个端点(蓝色)和一切点(黑色)。 转针的中点(红色)描绘了一个直径等于转针一半的长度的圆。 在数学 中,挂谷集合 (Kakeya set)或者贝西科维奇集合 ,是一个在欧几里德空间 中的点的集合,包含了在任何方向上的单位线段 。例如,欧几里德平面 中的一个半径为1/2的圆盘 ,或在三维空间 中一个半径为1/2的球,形成了一个挂谷集。 许多在此方面的研究已经研究了这样的点集面积最小值的问题。 贝西科维奇表明贝西科维奇集可以为无限小集。
挂谷转针集合(有时也称为挂谷集合)是一个在平面上的更典型的(贝西科维奇)集合,单位线段在其中可以连续旋转180度,使其与其原来的位置颠倒。半径为的1/2圆盘也是挂谷转针集合的一个例子。
挂谷转针问题,询问在平面上是否有一个面积最小的区域D ,在其中针可以旋转360度。挂谷宗一于1917年首次对于凸集 提出此问题。Pál的研究显示,凸集的最小面积可以通过一个高为1和面积为1/√3 的 等边三角形 达到。[ 1]
挂谷似乎认为面积最小的没有凸性限制的挂谷集 D 将是一个三尖瓣线 。然而这是错误的;还有较小的非凸挂谷集合。
一种“萌芽”方法,用于构造一个小尺度的挂谷集合。这里展示了两种可能的方法来划分我们的三角形并重叠部分以得到一个较小的集合,第一种方法是我们只使用两个三角形,第二种方法是我们使用八个三角形。请注意,与原始起始形状相比,最终形状的大小有多小。 亚伯兰·贝西科维奇 可以证明在其中单位长度的转针可以旋转一周的区域D 的面积没有一个大于0的下界。[ 2] 量度 的面积 。在此之前,分析学家可能已经考虑过这个问题。
一种构造贝西科维奇集合的方法(相关图形见图右)在奧斯卡·佩龍 能够简化贝西科维奇的原始结构之后被称作「佩龙树」:[ 3]
现在,想象我们把我们的三角形分为8个子三角形。对于每对相邻的三角形,重演如上所述的重叠过程,获得4个新图形,每个包括两个重叠的三角形。接着,将相邻的新图形移动,使其底部分重合,所以我们只剩下两个图形,最后用同样方法将这两个图形重合。最后,我们得到了一个看上去像是树之类的东西的图形,但面积远小于原来的三角形。
为了构造更小的点集,将三角形细分为2n −n ,并执行与我们之前两次和八次划分三角形时相同的操作。如果我们在每个三角形上所做的重叠量足够小,并且我们三角形的细分区域的大小n 足够大,我们就可以形成一棵我们想要的面积最小的树。一个贝西科维奇集合可以由等边三角形产生的佩隆树的三个旋转组合而成。
进一步采用该方法,我们可以构造一个集合序列,其交集是一个度量零的贝西哥维奇集合。这样做的一种方法是观察,如果我们有一个平行四边形,两个边在x =0和x =1线上,那么我们就可以找到一个平行四边形的并集,这些平行四边形的边也在这些线上,它们的总面积是任意小的,并且包含了平行四边形中将x =0上的一个点连接到x =1上的一个点的所有直线的平移。这可由贝西奥维奇的构造方法稍变化而得。重复以上,我们可以找到一个集合序列
K
0
⊇
K
1
⊇
K
2
⋯
{\displaystyle K_{0}\supseteq K_{1}\supseteq K_{2}\cdots }
每一个直线x =0和x =1之间的平行四边形的有限并集,其面积趋向于零,并且每一条都包含单位面积中连接x =0和x =1的所有直线的平移。这些集合的交集是一个包含所有这些线的转换的度量零集,因此这个交集的两个副本的并集是一个度量零的贝西科维奇集。
除了“萌芽”方法之外,还有其他方法可以构造贝西科维奇的度量零集。例如卡汉 康托尔集 在二维平面中构造一个贝西科维奇测量零点集。 [ 4]
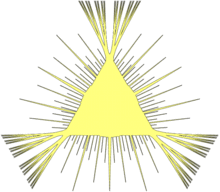
一个由佩龙树构造的挂谷转针集合
通过使用Pál 的技巧,即所谓的Pál连接 (给定两条平行线,任何单位线段都可以在任意小尺寸的集合上从一个连续移动到另一个),可以从由佩龙树组成的贝西科维奇集合创建一个单位线段可以在其中连续旋转180度的集合。[ 5]
1941年,H.J.van Alphen[ 6]
π
24
(
5
−
2
2
)
{\displaystyle {\tfrac {\pi }{24}}(5-2{\sqrt {2}})}
[ 7]
虽然有测量为任意小正数的挂谷转针集合和测量为0的贝西科维奇针组,但没有测量为0量的卡基亚针组。
然后,在更高维度中,也可以問最小的贝西科维奇集合有多大。這個問題衍生了许多称为挂谷猜想的猜想,并且开拓了称为几何测度论的数学领域。特别是,如果存在测度为零的贝西科维奇集,那么是否存在某些小于它们所处空间的维数的维度 s ,使得該挂谷集具有 s 维豪斯多夫测度零?这个问题产生了以下猜想:
挂谷集合猜想 :将R n 豪斯多夫维数 和闵科夫斯基维数 等于n.已知这对于n = 1,2是正确的,但是在更高维度中仅知道部分结果。
解决这个问题的一种现代方法是考虑一种特殊类型的最大函数,我们将其构造如下:将 S n −1R n
T
e
δ
(
a
)
{\displaystyle T_{e}^{\delta }(a)}
a ∈ R n e ∈ S n −1局部可积函数 f,我们定义f的挂谷极大值函数
f
∗
δ
(
e
)
=
sup
a
∈
R
n
1
m
(
T
e
δ
(
a
)
)
∫
T
e
δ
(
a
)
|
f
(
y
)
|
d
m
(
y
)
{\displaystyle f_{*}^{\delta }(e)=\sup _{a\in \mathbf {R} ^{n}}{\frac {1}{m(T_{e}^{\delta }(a))}}\int _{T_{e}^{\delta }(a)}|f(y)|dm(y)}
其中m 表示n维勒贝格度量 。请注意
f
∗
δ
{\displaystyle f_{*}^{\delta }}
S n − 然后对这些函数进行猜想,如果猜想是真的,将推出更高维度的挂谷集猜想:
挂谷极大函数猜想 :对于所有ε > 0,存在一个常数Cε > 0,这样对于任何函数f和所有δ> 0,(参见符号的lp空间)
‖
f
∗
δ
‖
L
n
(
S
n
−
1
)
⩽
C
ϵ
δ
−
ϵ
‖
f
‖
L
n
(
R
n
)
.
{\displaystyle \left\|f_{*}^{\delta }\right\|_{L^{n}(\mathbf {S} ^{n-1})}\leqslant C_{\epsilon }\delta ^{-\epsilon }\|f\|_{L^{n}(\mathbf {R} ^{n})}.}
以下是一些有利于证明挂谷猜想的成果:
挂谷猜想在n = 1 (平凡地)和n = 2 (Davies[ 8]
Wolff[ 9]
2000年,Katz 、Łaba 和陶哲轩 [ 10] 闵科夫斯基维数 在维数为3时严格地大于5/2。
2000年,讓·布爾甘 将挂谷问题与算术组合学 联系起来,[ 11] [ 12] 加法理论 。
2002年,Katz和陶哲轩[ 13]
(
2
−
2
)
(
n
−
4
)
+
3
{\displaystyle (2-{\sqrt {2}})(n-4)+3}
2017年,Katz和Zahl[ 14] 豪斯多夫维数 的下限推进到
5
/
2
+
ϵ
{\displaystyle 5/2+\epsilon }
ϵ
>
0
{\displaystyle \epsilon >0}
有些令人惊讶的是,这些猜想已经被证明与其他领域的一些问题有关,特别是在谐波 分析中。例如,在1971年,Charles Fefferman[ 15] Lp 范数
挂谷问题的一個類推,是要求集合包含其他形狀,例如圆形或球面,而非原問題的線段。
在1997年[ 16] [ 17] 有人猜想,存在一個零測集,其包含以每個點為中心的球面。然而,埃利亚斯·施泰因 [ 18] [ 19]
挂谷猜想的一个推广是考虑包含每個k维子空间的一部分的集合,而不是每个方向的线段。定義(n , k )-贝西科维奇集 K 为R n B 表示以零为中心的单位球,則对于每个k维子空间P ,存在x ∈ R n P ∩ B ) + x ⊆ K 。因此,(n , 1)-貝西科維奇集就是前面描述的标准貝西科維奇集。
(n , k )-貝西科維奇猜想: 对于k > 1,不存在(n , k )-貝西科維奇集。1979年,Marstrand[ 20] Falconer [ 21] k > n 时,不存在(n , k )-貝西科維奇集。截至2020年,最優的成果是,Bourgain[ 22] k −1k > n 时,不存在这样的集。
1999年,Wolff提出了Kakeya问题的有限域 模拟,希望解决这一猜想的技术可以推广到欧几里德情形。
有限域Kakeya猜想: 令F 为有限域,令K ⊆ F n 为挂谷集,即对于每个向量y ∈ F n x ∈ F n K 包含一条直线{x + ty : t ∈ F }。集合K 的大小至少为cn |F |n cn >0是只与n 有关常量。Zeev-Dvir在2008年证明了这个猜想,表明这个说法适用于cn = 1/n !。[ 23] [ 24] n 元次数低于|F |的为零的多项式必须为零。另一方面,次数低于|F |的n 元多项式形成有以下维数的向量空间:
(
|
F
|
+
n
−
1
n
)
≥
|
F
|
n
n
!
.
{\displaystyle {|\mathbf {F} |+n-1 \choose n}\geq {\frac {|\mathbf {F} |^{n}}{n!}}.}
因此,至少有一个次数小于 |F |的非平凡多项式在任何给定集上收敛,且点数小于此数。结合这两个观察结果,Kakeya集必须至少有|F |n n ! 个点。
现在仍未清楚这些技术是否会延伸到证明原始挂谷猜想,但这一证明确实使基本代数反例不太可能,从而为原始猜想提供了可信度。Dvir撰写了一篇关于有限域挂谷问题及其与随机抽取器 关系的综述文章。[ 25]
^ Pal, Julius. Ueber ein elementares variationsproblem. Kongelige Danske Videnskabernes Selskab Math.-Fys. Medd. 1920, 2 : 1–35. ^ Besicovitch, Abram . Sur deux questions d'integrabilite des fonctions. J. Soc. Phys. Math. 1919, 2 : 105–123. Besicovitch, Abram . On Kakeya's problem and a similar one. Mathematische Zeitschrift. 1928, 27 : 312–320. doi:10.1007/BF01171101 ^ Perron, O. Über eine Satz von Besicovitch. Mathematische Zeitschrift. 1928, 28 : 383–386. doi:10.1007/BF01181172 Falconer, K. J. The Geometry of Fractal Sets. Cambridge University Press. 1985: 96–99. ^ Kahane, Jean-Pierre . Trois notes sur les ensembles parfaits linéaires. Enseignement Math. 1969, 15 : 185–192. ^ The Kakeya Problem (页面存档备份 ,存于互联网档案馆 ) by Markus Furtner^ Alphen, H. J. Uitbreiding van een stelling von Besicovitch. Mathematica Zutphen B. 1942, 10 : 144–157. ^ Cunningham, F. The Kakeya problem for simply connected and for star-shaped sets (PDF) . American Mathematical Monthly (The American Mathematical Monthly, Vol. 78, No. 2). 1971, 78 (2): 114–129 [2019-03-09 ] . JSTOR 2317619 doi:10.2307/2317619 存档 (PDF) 于2020-09-21). ^ Davies, Roy. Some remarks on the Kakeya problem. Proc. Cambridge Philos. Soc. 69 (3): 417–421. Bibcode:1971PCPS...69..417D doi:10.1017/S0305004100046867 ^ Wolff, Thomas . An improved bound for Kakeya type maximal functions. Rev. Mat. Iberoamericana 11 : 651–674. doi:10.4171/rmi/188 ^ Katz, Nets Hawk; Laba, Izabella; Tao, Terence . An Improved Bound on the Minkowski Dimension of Besicovitch Sets in ℝ 3 . The Annals of Mathematics 152 (2): 383. doi:10.2307/2661389 ^ J. BOURGAIN, Harmonic analysis and combinatorics: How much may they contribute to each other?, Mathematics: Frontiers and Perspectives, IMU/Amer. Math. Soc., 2000, pp. 13–32.
^ Tao, Terence. From Rotating Needles to Stability of Waves: Emerging Connections between Combinatorics, Analysis and PDE (pdf) . Notices of the AMS 48 (3): 297–303 [2019-05-25 ] . (原始内容存档 (PDF) 于2010-07-02). ^ Katz, Nets Hawk; Tao, Terence. New bounds for Kakeya problems. J. Anal. Math. 87 : 231–263. arXiv:math/0102135 doi:10.1007/BF02868476 ^ Katz, Nets Hawk; Zahl, Joshua. An improved bound on the Hausdorff dimension of Besicovitch sets in ℝ3. 2017. arXiv:1704.07210 math.CA ]. ^ Fefferman, Charles . The multiplier problem for the ball . Annals of Mathematics 94 (2): 330–336. JSTOR 1970864 doi:10.2307/1970864 ^ Wolff, Thomas . A Kakeya problem for circles . American Journal of Mathematics. 1997, 119 (5): 985–1026. doi:10.1353/ajm.1997.0034 ^ Wolff, Thomas ; Wolff, Thomas. On some variants of the Kakeya problem. Pacific Journal of Mathematics. 1999, 190 : 111–154. doi:10.2140/pjm.1999.190.111 ^ Stein, Elias . Maximal functions: Spherical means . Proc. Natl. Acad. Sci. U.S.A. 1976, 73 (7): 2174–2175. Bibcode:1976PNAS...73.2174S PMC 430482 PMID 16592329 doi:10.1073/pnas.73.7.2174 ^ Marstrand, J. M. Packing circles in the plane. Proceedings of the London Mathematical Society. 1987, 55 : 37–58. doi:10.1112/plms/s3-55.1.37 ^ Marstrand, J. M. Packing Planes in R3 . Mathematika. 1979, 26 (2): 180–183. doi:10.1112/S0025579300009748 ^ Falconer, K. J. Continuity properties of k-plane integrals and Besicovitch sets. Math. Proc. Cambridge Philos. Soc. 1980, 87 (2): 221–226. Bibcode:1980MPCPS..87..221F doi:10.1017/S0305004100056681 ^ Bourgain, Jean . Besicovitch type maximal operators and applications to Fourier analysis. Geom. Funct. Anal. 1997, 1 (2): 147–187. doi:10.1007/BF01896376 ^ Dvir, Z. On the size of Kakeya sets in finite fields. J. Amer. Math. Soc. 2009, 22 : 1093–1097. doi:10.1090/S0894-0347-08-00607-3 ^ Terence Tao . Dvir’s proof of the finite field Kakeya conjecture . What's New. 2008-03-24 [2008-04-08 ] . (原始内容存档 于2020-11-11). ^ Dvir, Zeev. From Randomness Extraction to Rotating Needles. 2009. Template:ECCC .
Besicovitch, Abram . The Kakeya Problem. American Mathematical Monthly. 1963, 70 (7): 697–706. JSTOR 2312249 MR 0157266 doi:10.2307/2312249 Dvir, Zeev. On the size of Kakeya sets in finite fields. Journal of the American Mathematical Society . 2009, 22 (4): 1093–1097. Bibcode:2009JAMS...22.1093D MR 2525780 arXiv:0803.2336 doi:10.1090/S0894-0347-08-00607-3 Falconer, Kenneth J. The Geometry of Fractal Sets. Cambridge Tracts in Mathematics 85 . Cambridge: Cambridge University Press. 1985. ISBN 0-521-25694-1MR 0867284 Kakeya, Soichi. Some problems on maximum and minimum regarding ovals. Tohoku science reports. 1917, 6 : 71–88. Katz, Nets Hawk ; Łaba, Izabella ; Tao, Terence . An improved bound on the Minkowski dimension of Besicovitch sets in
R
3
{\displaystyle \mathbf {R} ^{3}}
(PDF) . Annals of Mathematics. 2000, 152 (2): 383–446. JSTOR 2661389 MR 1804528 doi:10.2307/2661389