度分布

英文维基条目网络的度分布。将每个条目看成顶点，超链接看成边，则对应的出度/入度的分布如图所示。

度分布是图论和网络理论中的概念。一个图（或网络）由一些顶点（节点）和连接它们的边（连结）构成。每个顶点（节点）连出的所有边（连结）的数量就是这个顶点（节点）的度。度分布指的是对一个图（网络）中顶点（节点）度数的总体描述。对于随机图，度分布指的是图中顶点度数的概率分布。

定义

度分布是图论和（复杂）网络理论中都存在的概念。首先介绍图的概念。一个图${\displaystyle G=G(V,E)}$是一个由两个集合${\displaystyle V}$和${\displaystyle E}$构成的二元组。集合${\displaystyle V}$一般由有限个元素构成：${\displaystyle V=\{v_{1},v_{2},\cdots ,v_{n}\}}$，其中的元素${\displaystyle v_{i},\,i=1,2,\cdots ,n}$被称为图的顶点。集合${\displaystyle E}$是由${\displaystyle n^{2}}$个元素构成的集合：${\displaystyle E=\{e_{i,j}\,\,|\,\,i=1,2,\cdots ,n,\,j=1,2,\cdots ,n\}}$。${\displaystyle E}$中的每个元素都是一个非负整数。无向图中，${\displaystyle E}$的一个元素${\displaystyle e_{i,j}=k}$，表示${\displaystyle V}$中的两个顶点${\displaystyle i}$和${\displaystyle j}$连有${\displaystyle k}$条边，并且规定${\displaystyle e_{i,j}=e_{j,i}}$。有向图中，${\displaystyle E}$的一个元素${\displaystyle e_{i,j}=k}$，表示${\displaystyle V}$中的顶点${\displaystyle i}$有${\displaystyle k}$条连向顶点${\displaystyle j}$的边。如果一个图${\displaystyle G}$中所有的${\displaystyle e_{i,j}}$都不超过1，并且${\displaystyle \forall i=1,2,\cdots ,n,\,\,e_{i,i}=0}$，那么称图${\displaystyle G}$是简单图。

网络理论的数学框架建立在图论上。网络理论中的网络其实就是图论中的图，但在网络理论中称之为网络，图的顶点在网络理论中称为节点，边被称为连结。以下仍旧以图论中的术语定义度分布。

一个无向图${\displaystyle G=G(V,E)}$中某个顶点${\displaystyle v_{i_{0}}}$的度，是指所有与它相连的边的数目。

${\displaystyle d(v_{i_{0}})=\sum _{i=i_{0}}e_{i,j}}$

有向图中，根据连出边的数目和连入边的数目，分为出度${\displaystyle d_{out}}$和入度${\displaystyle d_{in}}$。

${\displaystyle d_{out}(v_{i_{0}})=\sum _{i=i_{0}}e_{i,j}}$

${\displaystyle d_{in}(v_{i_{0}})=\sum _{j=i_{0}}e_{i,j}}$

因此，一个无向图${\displaystyle G=G(V,E)}$中，${\displaystyle d}$可以看成将每个顶点映射到一个非负整数的函数：

${\displaystyle d:\,v_{i}\mapsto d(v_{i})\quad i=1,2,\cdots ,n.}$

而度分布则是对每个非负整数${\displaystyle m}$，考察度数是${\displaystyle m}$的顶点在所有顶点中占的比例：

${\displaystyle \forall m\in \mathbb {N} ,\,\,P:m\mapsto P(m)={\frac {\operatorname {Card} \{v_{i}\,|\,d(v_{i})=m\}}{n}},}$[1]

因此满足：

${\displaystyle \sum _{m\in \mathbb {N} }P(m)=1.}$

从顶点中等概率地随机抽取一个顶点，那么这个顶点度数为${\displaystyle k}$的概率就是${\displaystyle P(k)}$。

随机图顶点的度分布

随机图是指由随机过程产生的图，即是将给定的顶点之间随机地连上边。一个随机图${\displaystyle G=G(V,E)}$中，每两个顶点之间的边的数量${\displaystyle e_{i,j}}$是随机变量。因此任一顶点${\displaystyle v_{i_{0}}}$的度${\displaystyle d(v_{i_{0}})=\sum _{i=i_{0}}e_{i,j}}$也是随机变量。这个变量的概率分布也称为随机图中的顶点的度分布：

${\displaystyle P_{i}(k)=\mathbb {P} (d(v_{i})=k).}$

这个定义与一般的图的度分布是不一样的[2]。

在经典的随机图模型中，所有顶点的位置都是一致的，没有特殊的顶点。因此每个顶点的度分布${\displaystyle P_{i}(k)}$都是相同的：${\displaystyle \forall i,\,P_{i}(k)=P(k)}$。所以，随机抽取一个顶点，它的度数是${\displaystyle k}$的概率就是${\displaystyle P(k)}$；${\displaystyle P(k)}$越高，表示可能有更多的顶点度数是${\displaystyle k}$。当顶点数目很大每个顶点的度分布都是相对独立的时候，顶点的度分布${\displaystyle P_{i}(k)}$近似等于图中度数是${\displaystyle k}$的顶点的比例[1]。

例子

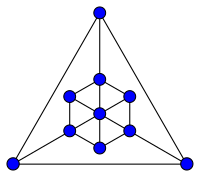
由十个顶点构成的图

以下给出一些度分布的例子。右图是由十个顶点构成的无向图。其中度数是4的顶点有3个，度数是3的顶点有6个，度数是6的顶点有1个，所以度分布是：

${\displaystyle P(m)={\begin{cases}0.3,&m=4\\0.6,&m=3\\0.1,&m=6\\0,&m\neq 3,4,6\end{cases}}}$

对于${\displaystyle n}$阶完全图，所有的顶点的度数都是${\displaystyle n-1}$，所以度分布是：

${\displaystyle P(m)={\begin{cases}1,&m=n-1\\0,&m\neq n-1\end{cases}}}$

图3.随机网络的度（a）集中在某个特定值${\displaystyle d_{c}}$附近，而无尺度网络的度分布（b）则遵守幂律分布

如果图${\displaystyle G}$是任意两顶点之间以概率${\displaystyle 0<p<1}$连边的随机图，那么每个顶点都有相同的度分布。

${\displaystyle P(m)={\binom {n-1}{m}}p^{m}(1-p)^{n-1-m}.}$[2]

这个分布是泊松分布。我们可以构造每个顶点的度数都是这样的概率分布的随机图模型。这样当顶点数很大的时候，度数是${\displaystyle k}$的顶点的个数占的比例大致是${\displaystyle P(k)}$。这个分布的特点是当k很小或很大的时候，${\displaystyle P(k)}$都近似于0，${\displaystyle P(k)}$的值在一个特定的值处达到高峰，然后回落。也就是说，大多数的顶点的度数在这个特定值左右。然而在真实的复杂网络中，人们观察到，度分布并不像这种随机图模型显示的，聚集在某个特定值周围，而是随着k增大而以多项式速度递减，也就是遵从所谓的幂律分布：

${\displaystyle P(k)\propto {\frac {1}{k^{\gamma }}}}$

也就是说${\displaystyle P(k)}$ 的概率反比于${\displaystyle k}$ 的某个幂次，其中${\displaystyle \gamma }$是某个正实数。这种网络特性被称为无尺度特性[3][4]。

参考文献

引用

1. Newman, M. E. J. The structure and function of complex networks. SIAM Review. 2003, 45 (2): 167–256. Bibcode:2003SIAMR..45..167N. arXiv:cond-mat/0303516 . doi:10.1137/S003614450342480. ^[永久失效連結]
2. M. E. J. Newman, S. H. Strogatz, D. J. Watts. Random Graphs with Arbitrary Degree Distribution and Their Applications. Phys. Rev. E. 2001, 64. doi:10.1103/PhysRevE.64.026118. 
3. 《科学美国人》中文版2003年7月. 无尺度网络. 集智集团. [2011-07-04]. （原始内容存档于2012-01-11）. 
4. Albert-László Barabási, Réka Albert. Emergence of Scaling in Random Networks (PDF). Science: 509–512. [2013-04-19]. doi:10.1126/science.286.5439.509. （原始内容 (PDF)存档于2021-09-23）. 

期刊文章

• Albert, R.; Barabasi, A.-L. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002, 74: 47–97. Bibcode:2002RvMP...74...47A. arXiv:cond-mat/0106096 . doi:10.1103/RevModPhys.74.47.  引文使用过时参数coauthors (帮助)
• Dorogovtsev, S.; Mendes, J. F. F. Evolution of networks. Advances in Physics. 2002, 51 (4): 1079–1187. Bibcode:2002AdPhy..51.1079D. arXiv:cond-mat/0106144 . doi:10.1080/00018730110112519.  引文使用过时参数coauthors (帮助)

书籍

• Shlomo Havlin, Reuven Cohen. Complex Networks: Structure, Robustness and Function. Cambridge University Press. 2010 [2013-04-20]. （原始内容存档于2011-10-04）. 

参见

• 图的连通性
• 集聚系数
• 複雜網路
• 無尺度網路
• 隨機圖
• 圖論