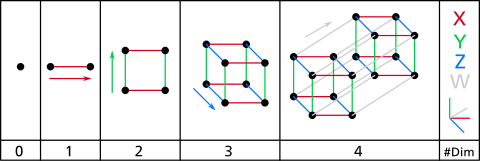在几何学 中,四維超正方体 或正八胞體 ,是一種四維 的超正方體 (英語:hypercube )是立方體 的四維類比,有8個立方體胞 。四維超正方体之於立方體,就如立方體之於正方形 。它是四維歐式空間中6個四維凸正多胞體 之一。
超正方体是一个有无穷多个成员的凸正多胞形 家族的四维成员,这个家族被称为“超方形 立方形 、正测形 ),这个家族的成员与施莱夫利符号{4,3,3,……,3,3},它们都具有类似正方形和立方体的性质,如二胞角都为90°等。
“超正方體”和“超立方體”(Hypercube)這個名稱在一般的場合中特指四維的這個超正方體,不過在數學上,“超正方體”這個詞可以指n維(n>3)的任意一個超方形 ,因此把它和n維的其他超方形放在一起討論時,要加“四維”以示區別。
四维超正方体的展开图 在四維歐幾里得空間 的標準四維方體是點(±1, ±1, ±1, ±1)的凸包 。它包含了點:
{
(
x
1
,
x
2
,
x
3
,
x
4
)
∈
R
4
:
−
1
≤
x
i
≤
1
}
{\displaystyle \{(x_{1},x_{2},x_{3},x_{4})\in \mathbb {R} ^{4}\,:\,-1\leq x_{i}\leq 1\}}
四維方體由八個超平面 (x i = ±1)包圍。兩兩非平行超平面相交,共形成四維方體的24個正方形面。每條棱有3個立方體和3個正方形相交。在每一頂點有4個立方體、6個正方形和4條棱相交。四維方體共有8個立方體、24個正方形、32條棱和16個頂點。边长为a的四维超正方体超体积是a4 ,表体积是8a3 。
若一个四维超立方体的棱长为1,则其外接超球半径为1,外中交超球(经过超立方体各棱中点的三维超球)半径为
3
2
{\displaystyle {\frac {\sqrt {3}}{2}}}
2
2
{\displaystyle {\frac {\sqrt {2}}{2}}}
1
2
{\displaystyle {\frac {1}{2}}}
超方形 ,其自身中心到任意一个k维元素的中心的距离为
a
n
−
k
2
{\displaystyle {\frac {a{\sqrt {n-k}}}{2}}}
四維方體的每一頂點與4條棱相鄰,所以四維方體的頂點圖 是正四面體 。所以四維方體的施萊夫利符號 是{4,3,3},前面兩個數字{4,3}代表其維面 為立方體 、後面兩個數字{3,3}代表其頂點圖為正四面體 。其對偶多胞體 是正十六胞體 ,施萊夫利符號是{3,3,4}。對偶多胞體維面 與頂點圖 交換,正十六胞體 的維面 變為正四面體、頂點圖變為立方體。
作为一个超方形 ,超立方体可被识别为不同对称群的多胞体:首先,它是四维的超方形——一个凸正多胞体 ——四维超立方体,对应施莱夫利符号{4,3,3},考克斯特符號 4 平面(即超方形—正轴形 对应的考克斯特平面 超正八面体对称性 阶 为384。同时,它也可被看作是立方体的四维棱柱,对应施莱夫利符号{4,3}×{},考克斯特符號 四維柱體柱 的一个,即4-4柱體柱,是两个正方形的乘积,对应施莱夫利符号{4}×{4},考克斯特符號
展示如何从点开始得到超正方体的图像 超正方体的构造方法可以通过以下方式来想象:
零维 :因為任何一點放大都是一條直線,所以任何一點都是屬於一維空間,而不屬於零維空間。一维 :两个点A和B可以被连接起来,我们就得到一个新的线段AB。从一维到二维 :两个平行的线段AB和CD可以被连接起来,我们就得到了一个正方形 ,以顶点为标记记作正方形ABCD。从二维到三维 :两个平行的正方形ABCD和EFGH可以被连接起来,我们就得到了一个立方体 ,以顶点标记为立方体ABCDEFGH。从三维到四维 :两个平行的立方体ABCDEFGH和IJKLMNOP可以被连接起来,我们于是就得到了一个超正方体,以顶点标记为超正方体ABCDEFGHIJKLMNOP。四維方體的结构不易想象,但可以投射至3維或2維空間。在我们将其投影到二维空间中后,把頂點位置調整,可以了解更多。如此獲得的圖像,不再反映四維方體空間構造,而是反映頂點間的聯繫。以下給出一些例子。
第一幅圖顯示四維方體本質上從結合2個立方體,連結對應頂點得來。第二幅圖反映出四維方體每條邊 等長,也可以看出立方體如何互相連結。第三幅圖按著每一頂點由最底一頂點出發沿着棱走的長度排列。如果我们是要将超正方体用作在并行计算 中连接不同处理器网络拓扑 基础,则这些图像会非常有用。在超正方体中任意两个顶点之间之间至多有4中不同的路程,并且这里有许多路径是等同的。二分图 ,就像正方形和立方体一样。
超正方体正对顶点的平行投影的凸包就是菱形十二面体 。在这个投影中每层的顶点数是1 4 6 4 1——是杨辉三角 的第4行。
超正方体平行投影 的凸包(不同的胞的表面被涂上了不同的颜色,背面的胞在这里未显示) 超正方体到三维空间的正对胞 的平行投影 有一个立方体 凸包。最近端的和最远端的胞被投影成了立方体凸包本身,而剩余6个立方体胞则被投影成了立方体的6个正方形 面。(因为它们平行于投影线)
超正方体到三维空间的正对面 的平行投影有一个长方体 (正四棱柱)凸包。2对胞被投影成了长方体凸包的上下两半,而剩余4个胞则投影成了正四棱柱凸包的侧面。
超正方体到三维空间的正对棱 的平行投影有一个正六棱柱 形的凸包。6个胞被投影成了菱形棱柱,它们在正六棱柱凸包中的排列方式就如同立方体正对顶点的平行投影中正方形面投影成的菱形 在六边形 凸包中的排列方式。剩余的2个胞被投影成了正六棱柱的两个底面。
超正方体到三维空间的正对顶点 的平行投影有一个菱形十二面体 凸包,事实上,我们正好有两种方法能将菱形十二面体分割成4个全等的平行六面体 ,因此菱形十二面体中共计有8个全等的平行六面体。超正方体在这种投影下胞的投影就正好是这8个平行六面体。这个投影的体积是超正方体所有投影中最大的。
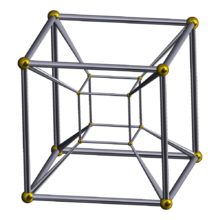
超立方体的施莱格尔投影
单旋转 透视投影 。
正交 的平面进行双旋转 四维空间 中最近的顶点,有4个立方体胞在此相交。
正四面体 是超正方体中心投影的凸包。8个立方体胞中的4个是可见的。第16个顶点被投影成了无穷远点 ,并且与之相连的棱和胞都被隐藏了。
球极投影 (棱首先被投影上了3-球 )
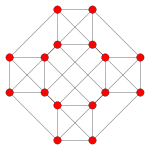
二维正交线架投影
考克斯特平面 B4
B3 / D4 / A2
B2 / D3
图像
二面体群
[8]
[6]
[4]
考克斯特平面
(对角线投向中心)
F4
A3
图像
二面体群
[2]
[12/3]
[4]
四维正多胞体
正五胞体 超立方体 正十六胞体 正二十四胞体 正一百二十胞体 正六百胞体
{3,3,3}
{4,3,3}
{3,3,4}
{3,4,3}
{5,3,3}
{3,3,5}
^ Unfolding an 8-cell . [2013-08-31 ] . (原始内容 存档于2018-07-25).