卡比博-小林-益川矩阵

卡比博-小林-益川矩阵（Cabibbo-Kobayashi-Maskawa，CKM或KM matrix）是粒子物理标准模型的一个重要组成成份，它表征了顶类型和底类型夸克间通过W粒子弱相互作用的耦合强度。对二代夸克情形，它是由意大利物理学家卡比博在1963年首先给出的，通常被称为卡比博矩阵或卡比博角。1973年日本物理学家小林诚和益川敏英把它推广到三代夸克。三代矩阵含有相位，可以用来解释弱相互作用中的电荷宇称对称性破缺（CP破坏），也被经常用来解释宇宙重子数不对称。CKM矩阵在轻子中的对应是牧-中川-坂田矩阵（Maki-Nakagawa-Sakata或MNS）。

内容

历史

早期的粒子物理模型包涵三种夸克—上夸克、下夸克和奇异夸克。在研究强子的弱衰变中，人们发现奇异数守恒的过程要比不守恒的过程进行得快约20倍。为解释此现象，卡比博引入了一个下夸克和奇异夸克（这两种夸克有相同的量子数）之间的混合角θ_c[1]。上夸克与下夸克和奇异夸克的相互作用耦合分别正比于此角的余弦（cosθ_c）和正弦（sinθ_c）。实验上sinθ_c约为0.23。

1973年，在一篇发表在日本期刊《理论物理学进展》上的题为“弱相互作用可重整化理论中的CP破坏”的论文中，小林诚和益川敏英把卡比博角推广到三代夸克[2]。他们发现虽然一般的三维幺正矩阵有九个实参数，但是只有四个具有物理意义，而其它的都可以被吸收到夸克波函数的位相中而不为观测。四个物理参数中的一个是位相因子，它提供了CP破坏的微观机制，同時猜测了第三代夸克的存在，因此具有重大的物理意义。他们二人也因而与南部阳一郎分享了2008年诺贝尔物理学奖[3][4]。

如今，寻找CKM矩阵参数的微观物理起源是粒子物理理论研究的重大课题之一。

参数化表示

CKM矩阵是一个三维幺正矩阵。 小林诚和益川敏英当初给的表示是[2]:

${\displaystyle {\begin{bmatrix}\cos \theta _{1}&-\sin \theta _{1}\cos \theta _{3}&-\sin \theta _{1}\sin \theta _{3}\\\sin \theta _{1}\cos \theta _{2}&\cos \theta _{1}\cos \theta _{2}\cos \theta _{3}-\sin \theta _{2}\sin \theta _{3}e^{i\delta }&\cos \theta _{1}\cos \theta _{2}\sin \theta _{3}+\sin \theta _{2}\cos \theta _{3}e^{i\delta }\\\sin \theta _{1}\sin \theta _{2}&\cos \theta _{1}\sin \theta _{2}\cos \theta _{3}+\cos \theta _{2}\sin \theta _{3}e^{i\delta }&\cos \theta _{1}\sin \theta _{2}\sin \theta _{3}-\cos \theta _{2}\cos \theta _{3}e^{i\delta }\end{bmatrix}}}$

在标准参数化下，它可以由三个混合角（θ₁₂，θ₁₃，θ₂₃）和一个相位（δ）表示为[5]

${\displaystyle {\begin{bmatrix}V_{ud}&V_{us}&V_{ub}\\V_{cd}&V_{cs}&V_{cb}\\V_{td}&V_{ts}&V_{tb}\end{bmatrix}}={\begin{bmatrix}c_{12}c_{13}&s_{12}c_{13}&s_{13}e^{-i\delta _{13}}\\-s_{12}c_{23}-c_{12}s_{23}s_{13}e^{i\delta _{13}}&c_{12}c_{23}-s_{12}s_{23}s_{13}e^{i\delta _{13}}&s_{23}c_{13}\\s_{12}s_{23}-c_{12}c_{23}s_{13}e^{i\delta _{13}}&-c_{12}s_{23}-s_{12}c_{23}s_{13}e^{i\delta _{13}}&c_{23}c_{13}\end{bmatrix}}.}$

其中（u，c，t）和（d，s，b）分别代表三代顶类型（上、粲、顶）和底类型（下、奇异、底）夸克，c₁₂，s₁₂等是cosθ₁₂，sinθ₁₂等的简写。 目前实验给出的数据：

θ₁₂ = 7001130399999999999♠13.04±0.05°

θ₁₃ = 6999201000000000000♠0.201±0.011°

θ₂₃ = 7000238000000000000♠2.38±0.06°

δ₁₃ = 7000120000000000000♠1.20±0.08

实验上CKM矩阵参数满足s₁₃<<s₂₃<<s₁₂<<1。 描写这一重要特性的一个常用参数化表示是由美国物理学家林肯·沃芬斯坦给出的。记

${\displaystyle s_{12}=\lambda ={\frac {|V_{us}|}{\sqrt {|V_{ud}|^{2}+|V_{us}|^{2}}}},\quad s_{23}=A\lambda ^{2}=\lambda \left|{\frac {V_{cb}}{V_{us}}}\right|,\,\,}$

${\displaystyle s_{13}e^{i\delta }=V_{ub}^{*}=A\lambda ^{3}(\rho +i\eta )={\frac {A\lambda ^{3}({\bar {\rho }}+i{\bar {\eta }})(1-A^{2}\lambda ^{4})^{1/2}}{(1-\lambda ^{2})^{1/2}[1-A^{2}\lambda ^{4}({\bar {\rho }}+i{\bar {\eta }})]}},}$

截止到λ^3，CKM矩阵为[6]

${\displaystyle {\begin{bmatrix}1-\lambda ^{2}/2&\lambda &A\lambda ^{3}(\rho -i\eta )\\-\lambda &1-\lambda ^{2}/2&A\lambda ^{2}\\A\lambda ^{3}(1-\rho -i\eta )&-A\lambda ^{2}&1\end{bmatrix}}.}$

么正三角形

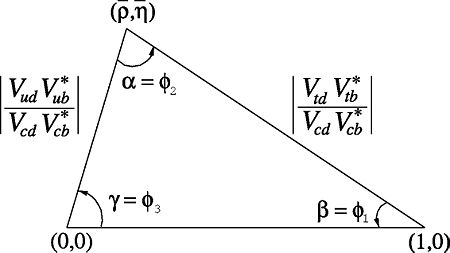
幺正三角形

CKM矩阵也可用所谓的幺正三角形来图像表示。最常见的是正交关系

${\displaystyle V_{ud}V_{ub}^{*}+V_{cd}V_{cb}^{*}+V_{td}V_{tb}^{*}=0}$

用测量最精确的项（V_cdV^*_cb）来归一，此关系可以表示为复平面上的三角形，其三顶点坐标分别为（0，0），（1，0） 和（${\displaystyle {\bar {\rho }}}$，${\displaystyle {\bar {\eta }}}$），如右图所示。它的面积与位相参数表示化无关，是刻划CP破坏的不变量。文献中称之为雅尔斯廓格（Jarlskog）不变量。

数学推导

CKM矩阵的数学推导相当平庸。首先任意一个三维矩阵可以写成欧拉形式V=V₂V₁V₃，其中对角块矩阵V₁，V₂，V₃有以下形式（X代表非零元）

${\displaystyle V_{1}={\begin{bmatrix}X&X&0\\X&X&0\\0&0&X\end{bmatrix}},\quad V_{2,3}={\begin{bmatrix}X&0&0\\0&X&X\\0&X&X\end{bmatrix}}}$

其次注意到任意一个二维幺正矩阵可以表为（ε，η，ρ为幺模复数，c=cosθ，s=sinθ）

${\displaystyle U={\begin{bmatrix}\epsilon c&\epsilon \eta s\\-\rho s&\rho \eta c\end{bmatrix}}}$

由此

${\displaystyle {\begin{bmatrix}\epsilon ^{*}&0\\0&\rho ^{*}\end{bmatrix}}U{\begin{bmatrix}1&0\\0&\eta ^{*}\end{bmatrix}}={\begin{bmatrix}c&s\\-s&c\end{bmatrix}}}$

因此可以通过一系列对角幺正矩阵作矩阵变换

${\displaystyle V\rightarrow DVD'=DV_{2}D''D''^{*}V_{1}D'''^{*}D'''V_{3}D'=V_{2}'V_{1}'V_{3}'}$

使得

${\displaystyle V_{2}'={\begin{bmatrix}1&0&0\\0&c_{2}&-s_{2}\\0&s_{2}&c_{2}\end{bmatrix}},\quad V_{3}'={\begin{bmatrix}1&0&0\\0&c_{3}&s_{3}\\0&-s_{3}&c_{3}\end{bmatrix}}}$

在上式中V₂'仍是与V₂同形的一般幺正矩阵， 但可以继续在V上左、右相乘与V₂'和V₃'对易的对角矩阵，即 diag（α，β，β）型矩阵（α，β幺模），使得

${\displaystyle V_{1}'={\begin{bmatrix}c_{1}&s_{1}&0\\-s_{1}&c_{1}&0\\0&0&e^{i\delta }\end{bmatrix}}}$

最后将所有的对角（相位）变换矩阵吸收到夸克波函数中去，V₂'，V₁'，V₃'相乘即得CKM矩阵。

参数测量

CKM矩阵元实验测定和最新数据的详细资料，可参阅粒子数据组的网页和出版物[7]

${\displaystyle V_{CKM}={\begin{bmatrix}0.97427\pm 0.00015&0.22534\pm 0.00065&0.00351_{-0.00014}^{+0.00015}\\0.22520\pm 0.00065&0.97344\pm 0.00016&0.0412_{-0.0005}^{+0.0011}\\0.00867_{-0.00031}^{+0.00029}&0.0404_{-0.0005}^{+0.0011}&0.999146_{-0.000046}^{+0.000021}\end{bmatrix}}.}$

沃尔芬斯坦参数：${\displaystyle \lambda =0.22535\pm 0.00065,A=0.817\pm 0.015,{\bar {\rho }}=0.136\pm 0.018,{\bar {\eta }}=0.348\pm 0.014}$

和雅尔斯廓格不变量：${\displaystyle J=(2.96_{-0.16}^{+0.20})\times 10^{-5}}$

獨立變量的計算

考慮有 N 代夸克 (2N 種風味)，那麼

• 一個 N × N 的么正矩陣需要 N^2 個實係數來給定 (因為么正矩陣滿足 VV^† = I，其中 V^† 是 V 的共軛轉置，而 I 是單位矩陣) 。
• 其中 2N − 1 個係數不是物理上實際的，因為每個夸克都可以吸收一個相位 (質量本徵態和弱作用力本徵態各可吸收一個)，而全部的共同相位是不可觀測的。因此，不受相位選擇影響的自由變數總共有 N^2 − (2N − 1) = (N − 1)^2 個。
  • 這其中有 N(N − 1)/2 個是旋轉角度，稱為夸克的混合角。
  • 而剩下的 (N − 1)(N − 2)/2 個就是造成 CP破壞的複數相位。

當 N = 2 時，獨立變量只有一個，就是兩代夸克間的混合角。當初只有兩代夸克被發現時，這是第一種 CKM 矩陣。其角度稱為卡比博角度，由尼古拉·卡比博發明。

在標準模型中，N = 3，總共有三個混合角和一個 CP 破壞相位。

与重子生成的关系

CP破坏是解釋自宇宙大爆炸以來僅物質存在(即反物質消失)的沙卡洛夫三条件（热力学非平衡，重子数不守恒，C和CP对称性不守恒）之一，因此CKM矩阵在粒子宇宙学中有着重要应用。但是现在公认的结论是實驗測量到CP破壞的數量級，遠不足以解释观测到的重子不对称度，因此重子生成必须有其他的来源。

参考资料

书籍

• 郑大培，李靈峰. Gauge Theory of Elementary Particle Physics [基本粒子物理的规范理论]. 牛津大学出版社. 1989. ISBN 0-19-851956-7. 
• H. Georgi. Weak Interactions and Modern Particle Physics [弱相互作用和现代粒子物理学]. Addison-Wesley. 1984. ISBN 0-8053-3163-8. 

论文

1. N. Cabibbo. Unitary Symmetry and Leptonic Decays. Physical Review Letters. 1963, 10: 531–533. 
2. M. Kobayashi and T. Maskawa. CP Violation in the Renormalizable Theory of Weak Interaction. Progress in Theoretical Physics. 1973, 49: 652–657. 
3. The Nobel Prize in Physics 2008. Nobel Foundation. [2008-10-09]. （原始内容存档于2008-10-08）. 
4. 闫同民. 与2008年诺贝尔物理奖失之交臂的物理学家. 物理双月刊: 354–357. 2013 [2013-10-02]. （原始内容存档于2013-10-04）.  参数|journal=与模板{{cite web}}不匹配（建议改用{{cite journal}}或|website=） (帮助); |volume=被忽略 (帮助)
5. L.L. Chau and W.-Y. Keung. Comments on the Parametrization of the Kobayashi-Maskawa Matrix. Physical Review Letters. 1984, 53: 1802. 
6. L. Wolfenstein. Parameterization of the Kobayashi-Maskawa Matrix. Physical Review Letters. 1983, 51: 1945–1947. 
7. K. Nakamura; et al. Review of Particles Physics: The CKM Quark-Mixing Matrix (PDF). Journal of Physics G. 2010, 37 (75021): 150 [2012-11-05]. （原始内容存档 (PDF)于2018-07-14）.  引文格式1维护：显式使用等标签 (link)

外部链接

• 粒子物理数据组（页面存档备份，存于互联网档案馆）首頁
• 康奈尔大学的CLEO（页面存档备份，存于互联网档案馆）实验
• 高能加速器研究機構 (KEK（页面存档备份，存于互联网档案馆）) 的 BELLE（页面存档备份，存于互联网档案馆） 實驗
• SLAC国家加速器实验室 (SLAC（页面存档备份，存于互联网档案馆）) 的 BaBar（页面存档备份，存于互联网档案馆） 實驗
• 费米国家加速器实验室（FNAL（页面存档备份，存于互联网档案馆））的D0（页面存档备份，存于互联网档案馆）和CDF（页面存档备份，存于互联网档案馆）实验
• 欧洲核子研究中心（CERN（页面存档备份，存于互联网档案馆））的LHCb（页面存档备份，存于互联网档案馆） 实验