Список моментів інерції

Нижче приведено список формул, за якими розраховуються моменти інерції різних тіл. Розмірність масових моментів інерції — маса×довжина^2. Це обертовий аналог маси тіл. Ці моменти інерції не слід плутати із моментами інерції плоских перерізів, які використовуються при розрахунку згинів і деформацій.

Нижченаведені моменти інерції допускають лише сталу густину тіл обертання, а вісь обертання проведена через центр мас, якщо не зазначено інше

Опис	Фігура	Момент(и) інерції	Коментар
Точкова маса m на відстані r від осі обертання.		${\displaystyle I=mr^{2}}$	Точка не має моменту інерції відносно осі, що проходить крізь неї. Наведений вираз отримано з теореми Штейнера.
Дві точкові маси, M і m, із зведеною масою ${\displaystyle \mu }$ на віддалі, x одна від одної.		${\displaystyle I={\frac {Mm}{M\!+\!m}}x^{2}=\mu x^{2}}$	—
Стрижень довжиною L і масою m (Вісь обертання проходить через один із кінців стрижня)		${\displaystyle I_{\mathrm {end} }={\frac {mL^{2}}{3}}\,\!}$  [1]	В цьому виразі припускається що стрижень нескінченно тонкий (однак твердий). Це також є частковим випадком тонкої прямокутної площини з осями обертання на краю площини з h = L і w = 0.
Стрижень довжиною L і масою m		${\displaystyle I_{\mathrm {center} }={\frac {mL^{2}}{12}}\,\!}$  [1]	В цьому виразі припускається що стрижень нескінченно тонкий (однак твердий). Це також є частковим випадком тонкої прямокутної площини з осями обертання що проходять через центр площини, w = L і h = 0.
Тонке кільце радіусу r маси m		${\displaystyle I_{z}=mr^{2}\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{2}}\,\!}$	Це частковий випадок тора для якого b=0. (див. нижче), а також тонкостінного циліндра без основ, з r1=r2 і h=0.
Тонкий суцільний диск, радіусу r і маси m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$ ${\displaystyle I_{x}=I_{y}={\frac {mr^{2}}{4}}\,\!}$	Це частковий випадок суцільного циліндра,з h=0.
Тонка циліндрична оболонка з без основ, радіусу r маси m		${\displaystyle I=mr^{2}\,\!}$  [1]	Цей вираз говорить що товщина оболонки нескінченно мала. Це частковий випадок тонкостінної циліндричної труби для r1=r2. Також, точкова маса (m) на кінці стрижня довжиною r має саме такий момент інерції а значення r називають радіусом інерції .
Суцільний циліндр радіусу r, висоти h і маси m		${\displaystyle I_{z}={\frac {mr^{2}}{2}}\,\!}$  [1] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left(3r^{2}+h^{2}\right)}$	Це частковий випадок тонкостінної циліндричної труби з r1=0. (Зауваження: осі X-Y повинні помінятися місцями для стандартної правої трійки базисних векторів)
Тонкостінна циліндрична труба з без основ з внутрішнім радіусом r1, зовнішнім радіусом r2, довжиною h і масою m		${\displaystyle I_{z}={\frac {1}{2}}m\left({r_{1}}^{2}+{r_{2}}^{2}\right)}$  [1][2] ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}m\left[3\left({r_{2}}^{2}+{r_{1}}^{2}\right)+h^{2}\right]}$ або ж вводячи нормовану товщину tn = t/r і припускаючи r = r2, then ${\displaystyle I_{z}=mr^{2}\left(1-t_{n}+{\frac {1}{2}}{t_{n}}^{2}\right)}$	З густиною ρ і такою ж геометрією ${\displaystyle I_{z}={\frac {1}{2}}\pi \rho h\left({r_{2}}^{4}-{r_{1}}^{4}\right)}$ ${\displaystyle I_{x}=I_{y}={\frac {1}{12}}\pi \rho h\left(3({r_{2}}^{4}-{r_{1}}^{4})+h^{2}({r_{2}}^{2}-{r_{1}}^{2})\right)}$
Сфера (пустотіла) радіуса r і маси m		${\displaystyle I={\frac {2mr^{2}}{3}}\,\!}$  [1]	Пустотіла сфера може розглянута такою, що зроблена з двох наборів нескінченно-тонких, круглих обручів, в яких радіус змінюється від 0 до r (або одного набору, в якого радіус змінюється з -r до r).
Куля (суцільна) радіусу r і маси m		${\displaystyle I={\frac {2mr^{2}}{5}}\,\!}$  [1]	Сфера може розглядатись як така, що зроблена з двох наборів нескінченно-тонких твердих дисків в яких радіус змінюється від 0 до r (або одного набору в якого радіус змінюється від -r до r). Також, може розглядатись як зроблена з нескінченно тонких, пустотілих сфер, де радіус змінюється від 0 до r.
Прямокутний Конус радіусу r висоти height h і маси m.		${\displaystyle I_{z}={\frac {3}{10}}mr^{2}\,\!}$  [3] ${\displaystyle I_{x}=I_{y}={\frac {3}{5}}m\left({\frac {r^{2}}{4}}+h^{2}\right)\,\!}$  [3]	—
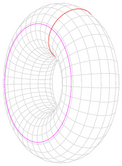
Трубчатий тор радіусу а, з радіусом перерізу b і маси m.		Навколо діаметра: ${\displaystyle {\frac {1}{8}}\left(4a^{2}+5b^{2}\right)m}$  [4] Навколо вертикальної осі: ${\displaystyle \left(a^{2}+{\frac {3}{4}}b^{2}\right)m}$  [4]	—
Еліпсоїд (суцільний) з напівосями a, b, і c з віссю обертання a і масою m		${\displaystyle I_{a}={\frac {m(b^{2}+c^{2})}{5}}\,\!}$	—
Тонка прямокутна площина висоти h і ширини w і маси m (Вісь обертання на краю площини)		${\displaystyle I_{e}={\frac {mh^{2}}{3}}+{\frac {mw^{2}}{12}}\,\!}$	—
Тонка прямокутна площина висоти h і ширини w і маси m		${\displaystyle I_{c}={\frac {m(h^{2}+w^{2})}{12}}\,\!}$  [1]	—
Суцільний кубоїд висоти h, ширини w, і глибини depth d, маси m		${\displaystyle I_{h}={\frac {1}{12}}m\left(w^{2}+d^{2}\right)}$ ${\displaystyle I_{w}={\frac {1}{12}}m\left(h^{2}+d^{2}\right)}$ ${\displaystyle I_{d}={\frac {1}{12}}m\left(h^{2}+w^{2}\right)}$	Для схоже орієнтованого куба з ребрами ${\displaystyle s}$, ${\displaystyle I_{CM}={\frac {ms^{2}}{6}}\,\!}$.
Суцільний кубоїд висоти D, ширини W, довжини L, і маси m з найдовшою діагоналлю в ролі осі обертання.		${\displaystyle I={\frac {m\left(W^{2}D^{2}+L^{2}D^{2}+L^{2}W^{2}\right)}{6\left(L^{2}+W^{2}+D^{2}\right)}}}$	Для куба з ребрами ${\displaystyle s}$, ${\displaystyle I={\frac {ms^{2}}{6}}\,\!}$.
Плоский многокутник з вершинами ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ і масою ${\displaystyle m}$ однорідно розподіленою на його поверхні, що обертається навколо осі перпендикулярній до площини і проходить через початок координати.		${\displaystyle I={\frac {m}{6}}{\frac {\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|(({\vec {P}}_{n+1}\cdot {\vec {P}}_{n+1})+({\vec {P}}_{n+1}\cdot {\vec {P}}_{n})+({\vec {P}}_{n}\cdot {\vec {P}}_{n}))}{\sum \limits _{n=1}^{N-1}\|{\vec {P}}_{n+1}\times {\vec {P}}_{n}\|}}}$	Цей вираз передбачає, що многокутник є опуклим. Вектори ${\displaystyle {\vec {P}}_{1}}$, ${\displaystyle {\vec {P}}_{2}}$, ${\displaystyle {\vec {P}}_{3}}$, ..., ${\displaystyle {\vec {P}}_{N}}$ є радіус-векторами вершин.
Нескінченний круг з масою, що нормально розподілена на двох осях навколо обертання (тобто ${\displaystyle \rho (x,y)={\tfrac {m}{2\pi ab}}\,e^{-((x/a)^{2}+(y/b)^{2})/2}}$ де : ${\displaystyle \rho (x,y)}$ — масова густина як функція x і y).		${\displaystyle I=m(a^{2}+b^{2})\,\!}$	—

Див. також

• Теорема Штейнера
• Махове колесо

Примітки

1. Raymond A. Serway (1986). Physics for Scientists and Engineers, second ed. Saunders College Publishing. с. 202. ISBN 0-03-004534-7.
2. Classical Mechanics - Moment of inertia of a uniform hollow cylinder. LivePhysics.com. Retrieved on 2008-01-31.
3. Ferdinand P. Beer and E. Russell Johnston, Jr (1984). Vector Mechanics for Engineers, fourth ed. McGraw-Hill. с. 911. ISBN 0-07-004389-2.
4. Eric W. Weisstein. Moment of Inertia — Ring. Wolfram Research. Архів оригіналу за 13 липня 2013. Процитовано 25 березня 2010.