uk %D0%94%D0%BE%D0%B1%D1%83%D1%82%D0%BE%D0%BA (%D1%82%D0%B5%D0%BE%D1%80%D1%96%D1%8F %D0%BA%D0%B0%D1%82%D0%B5%D0%B3%D0%BE%D1%80%D1%96%D0%B9)

Добуток (категорний добуток) — в теорії категорій це узагальнення таких понять декартів добуток множин, прямий добуток груп і добуток топологічних просторів.

Добуток сімейства об'єктів — це найбільш загальний об'єкт, з якого який існує морфізм до кожного об'єкта сімейства. Добуток об'єктів двоїстий їхньому кодобутку, тобто визначення кодобутків можна отримати з визначення добутку обертанням усіх стрілок.

Визначення

Якщо $X 1$ та $X 2$ — об'єкти категорії $C$ , тоді об'єкт $X$ є добутком $X 1$ та $X 2$ , позначається $X 1 \times X 2$ , якщо він задовільняє універсальну властивість:

існують морфізми

π 1 : X \to X 1

,

π 2 : X \to X 2

такі, що для кожного об'єкту

Y

та пари морфізмів

f 1 : Y \to X 1

,

f 2 : Y \to X 2

існує єдиний морфізм

f : Y \to X

такий, що наступна діаграма є комутативною :

Єдиний морфізм $f$ називається добутком морфізмів $f 1$ та $f 2$ і позначається $< f 1, f 2 >$ . Морфізми $π 1$ та $π 2$ називаються канонічними проєкціями чи морфізмами проєкції.

Добуток більше ніж двох об'єктів визначається для сімейства об'єктів, яке індексоване множиною $I$ .

Об'єкт $X$ є добутком сімейства об'єктів $(X i) i \in I$ якщо існують морфізми $π i : X \to X i$ , такі, що для кожного об'єкта $Y$ та $I$ -індексованого сімейства морфізмів $f i : Y \to X i$ існує єдиний морфізм $f : Y \to X$ такий, що наступна діаграма є комутативною для всіх $i \in I$ :

Приклади

У категорії Set прямий добуток A і B — це добуток в сенсі теорії множин $A\times B$ , а пряма сума — диз'юнктне об'єднання $A\sqcup B$ .
У категорії Ring пряма сума — це тензорний добуток $A\otimes B$ , а прямий добуток — сума кілець $A\oplus B$ .
У категорії Vect_K прямий добуток і пряма сума ізоморфні — це сума векторних просторів $A\oplus B$ .

Властивості

...

Дистрибутивність

В категорії із скінченними добутками та кодобутками існує канонічний морфізм X×Y+X×Z → X×(Y+Z), тут знак плюс означає кодобуток. Це випливає із існування канонічних проєкцій і вкладень та з комутативності наступної діаграми: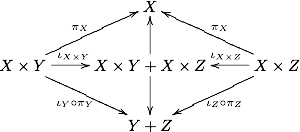

Властивість універсальності для X×(Y+Z) гарантує єдиність морфізму X×Y+X×Z → X×(Y+Z). Категорія називається дистрибутивною, якщо у ній цей морфізм є ізоморфізмом.

X\times (Y+Z)\simeq (X\times Y)+(X\times Z).

Див. також

Категорія добутку

Література