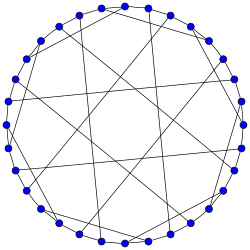
Граф Діка

Граф Діка
Граф Діка
Названо на честь	Вальтер фон Дік
Вершин	32
Ребер	48
Радіус	5
Діаметр	5
Обхват	6
Автоморфізм	192
Хроматичне число	2
Хроматичний індекс	3
Число черг	2
Властивості	симетричний кубічний гамільтонів двочастковий граф Келі

Граф Діка — це 3-регулярний граф з 32 вершинами і 48 ребрами, названий на честь Вальтера фон Діка. Граф є гамільтоновим графом з 120 різними гамільтоновими циклами. Його хроматичне число дорівнює 2, хроматичний індекс дорівнює 3, його радіус дорівнює 5, діаметр дорівнює 5 і обхват дорівнює 6. Він є також 3-вершинно-зв'язним і 3-реберно-зв'язним.

Граф Діка є тороідальним, і двоїстий граф його тороїдального вкладення — це граф Шрікханде, суворо регулярний симетричний гамільтонів граф.

Алгебраїчні властивості

Група автоморфізмів графу Діка — це група порядку 192. Вона діє транзитивно на вершини і ребра графу. Таким чином, граф Діка є симетричним. Він має автоморфізм, які переводять будь-яку вершину в будь-яку іншу вершину і будь-яке ребро в будь-яке інше ребро. У списку Фостера граф Діка, позначений як F32A, є єдиним кубічним симетричним графом з 32 вершинами.

Характеристичний многочлен графу Діка дорівнює (х-3)(х-1)^9 (x+1)^9 (x+3)(x*x-5)^6 .

Карта Діка

Граф Діка є кістяком симетричного паркету поверхні третього роду з дванадцяти восьмикутників, відомого як карта Діка або Паркет Діка. Двоїстий граф цього паркету є повним тридольним графом K4,4,4.

Галерея

• 
  Альтернативне зображення графу Діка
• 
  Хроматичне число графу Діка дорівнює 2
• 
  Хроматичний індекс графу Діка дорівнює 3

Примітки

1. ↑ W. Dyck Über Aufstellung und Untersuchung von Gruppe und Irrationalität regulärer Riemann'scher Flächen // Math. Ann.. — Т. 17. — DOI: http://link.springer.com/article/10.1007%2FBF01446929^[недоступне посилання з липня 2019]
2. ↑ Weisstein, Eric W. Dyck Graph (англ.) на сайті Wolfram MathWorld.
3. ↑ Royle, G. F032A data
4. ↑ M. Conder, P. Dobcsányi Trivalent symmetric graphs up to 768 vertices // J. Combin. Math. Combin. Comput.. — 2002. — Т. 40. — С. 41–63.
5. ↑ W. Dyck Notiz über eine reguläre Riemannsche Fläche vom Geschlecht 3 und die zugehörige Normalkurve 4. Ordnung // Math. Ann.. — 1880. — Т. 17. — С. 510—516.
6. ↑ A. Ceulemans The tetrakisoctahedral group of the Dyck graph and its molecular realization. // Molecular physics. — 2004. — Т. 102, вип. 11. — С. 1149—1163. — DOI: http://www.tandfonline.com/doi/abs/10.1080/00268970410001728780^[недоступне посилання з липня 2019]