Графи Чана

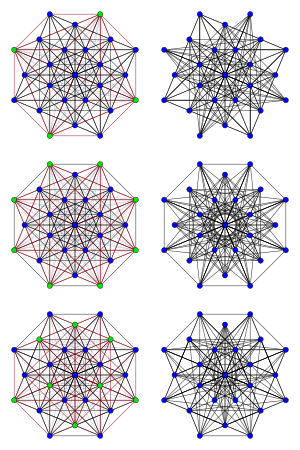
Графи Чана
Три графи Чана (праворуч) і перемикальні множини, що генерують їх із реберного графа ${\displaystyle L(K_{8})}$ (зелені вершини ліворуч)
Названо на честь	Лі-Чієна Чана
Вершин	28
Ребер	168
Радіус	2
Діаметр	2
Обхват	3
Автоморфізм	96360384
Властивості	сильно регулярний

Графи Чана — це набір із трьох 12-регулярних неорієнтованих графів, кожен із 28 вершинами та 168 ребрами. Усі вони сильно регулярні і мають такі ж параметри та спектр, як і реберний граф ${\displaystyle L(K_{8})}$ повного графа ${\displaystyle K_{8}}$. Графи Чана названо ім'ям Лі-Чієна Чана (англ. Chang Li-Chien), який довів, що, за винятком цих трьох графів, будь-який реберний граф повного графа єдиним чином визначається його параметрами сильно регулярного графа[1].

Зв'язок із графами L(K₈)

Кожен із цих трьох графів можна отримати перемиканням графа з ${\displaystyle L(K_{8})}$. Тобто, вибирається підмножина ${\displaystyle S}$ вершин графа ${\displaystyle L(K_{8})}$, кожне ребро, яке з'єднує вершину з ${\displaystyle S}$ із вершиною не з ${\displaystyle S}$ у графі ${\displaystyle L(K_{8})}$, видаляється і додаються ребра для кожної пари вершин (знову ж одна належить ${\displaystyle S}$, а інша не належить), які раніше не були з'єднані ребром. Серед графів, які можна утворити в такий спосіб, є графи Чана.

Див. також

• Граф Шрікханде, схоже виключення єдиності параметрів сильно регулярних графів ${\displaystyle L(K_{n},n)}$

Примітки

1. Chang, 1959, с. 604–613.

Література

• Chang Li-Chien. The uniqueness and non-uniqueness of the triangular association schemes // Science Record (Peking). — 1959. — Т. 3. — (New. Ser.).

Посилання

• Weisstein, Eric W. «Chang Graphs.» From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/ChangGraphs.html Архівовано січень 28, 2019 на сайті Wayback Machine.
• Andries E. Brouwer's page on Chang graphs Архівовано квітень 11, 2018 на сайті Wayback Machine.
• Nadia Hamoud, «The Chang graphs» Архівовано серпень 29, 2017 на сайті Wayback Machine.