uk %D0%91%D1%96%D1%82%D0%BE%D0%B2%D0%B8%D0%B9 %D0%B7%D1%81%D1%83%D0%B2

Бітовий зсув ― зміна позицій бітів у машинному слові на одну і ту ж величину.

Більшість комп'ютерів не можуть напряму адресувати біти, які містяться групами по 8, 16, 32 або 64 бітів у машинних словах. Для забезпечення роботи з бітами існує багато машинних інструкцій, що включають різні типи зсувів. Всі зсуви схожі між собою поведінкою середніх бітів, які просто зсуваються вліво або вправо на певну величину. Однак, поведінка крайніх бітів, які виходять зі слова та які з'являються в слові, залежить від типу зсуву.

В електроніці бітові зсуви здійснюються в регістрах зсуву.

Логічний зсув

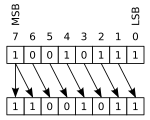
Логічний зсув — це зсув, за якого біт, який зсувається, зникає не впливаючи на біти, що залишились, а замість нього записується 0.

Приклад виконання логічного зсуву:

нехай є число 10101010b (в двійковій системі);

після зсуву вліво на 1 біт отримаємо число 01010100b;

після зсуву початкового числа вправо на 1 біт отримаємо число 01010101b.

У більшості процесорів біт, що зсувається зберігається у прапорі переносу. Ця функція використовується для роботи з багатобайтовими числами.

Арифметичний зсув

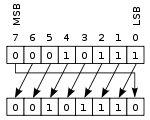
При цьому зсуві слово розглядається не просто як група бітів, а як ціле число в доповняльному коді. Зсув вліво виконується як логічний зсув, а під час зсуву вправо біт, що виходить, зникає, не впливаючи на біти, що залишилися, а на місце біта, що з'явився, встановлюється біт, відповідний знаку.

Приклад виконання арифметичного зсуву:

нехай є число 11111010b = -6 (у двійковій системі);

Після зсуву вліво на 1 біт отримаємо число 11110100b = -12;

Після зсуву початкового числа вправо на 1 біт отримаємо число 11111101b = -3.

Легко помітити, що, за арифметичного зсуву, зсув вліво відповідає множенню на 2, а зсув вправо ― діленню на 2 (в загальному випадку — на основу системи числення) з округленням до -∞. Наприклад:

 1011 = -5          1111 = -1 
>> a 1             >> a 1 
 -------- 
 1101 = -3          1111 = -1

Схемотехнічна реалізація операцій зсуву дуже проста. Саме тому ці операції рекомендують використовувати для операцій множення і ділення цілих чисел на числа, рівні степеням 2 (2, 4, 8, 16, 32, 64 і т. д.), якщо, звичайно, не заважає таке округлення від'ємних чисел.

Циклічний зсув

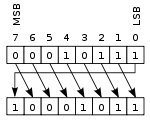
Під час цього зсуву біт, що виходить, з'являється на місці того біта, який з'явився.

Приклад виконання циклічного зсуву:

нехай є число 11111010b (у двійковій системі);

після зсуву вліво на 1 біт отримаємо число 11110101b;

після зсуву початкового числа вправо на 1 біт отримаємо число 01111101b.

Циклічний зсув через біт переносу

В архітектуру багатьох процесорів входить прапор переносу до наступного розряду (наприклад, cf на x86). Ця операція виконує циклічний зсув над (n+1)-бітовим числом, що складається з регістра і прапора переносу.

Наприклад, якщо в регістрі число 11111010b, а прапор переносу дорівнює 0:

після зсуву вліво на 1 біт: у регістрі 11110100b, прапор переносу дорівнює 1;

після зсуву вправо на 1 біт: у регістрі 01111101b, прапор переносу дорівнює 0.

Операція циклічного зсуву через біт переносу використовується для роботи з багатобайтовими числами. Зокрема, щоб зсунути вправо на 1 біт довге число, потрібно очистити^[1] cf (у разі ділення числа зі знаком потрібно записати в cf старший біт старшого слова) і циклічно зсунути на одиницю через cf кожне слово, починаючи з верхнього.

Наприклад, нехай є число 011000111100b, що займає три 4-бітових слова:

Було: HI = 0110, MED = 0011, LO = 1100, cf = 0 
Після зсуву HI: HI = 0011, MED = 0011, LO = 1100, cf = 0 
Після зсуву MED: HI = 0011, MED = 0001, LO = 1100, cf = 1 
Після зсуву LO: HI = 0011, MED = 0001, LO = 1110, cf = 0

Зсув через регістр прапорів більш ніж на 1 біт практично не використовують.

Див. також

Примітки

↑ Можна замість очищення прапора для першого оброблюваного слова використати арифметичний/логічний зсув, якщо він присвоює прапору cf значення біта, який вийшов.

Посилання

«Assembler & Win32. Курс молодого бійця.» Урок 11. «Біти, зсув логічний, арифметичний і циклічний.» [Архівовано 5 жовтня 2012 у Wayback Machine.]

Це незавершена стаття про інформаційні технології.
Ви можете допомогти проєкту, виправивши або дописавши її.

[1] Можна замість очищення прапора для першого оброблюваного слова використати арифметичний/логічний зсув, якщо він присвоює прапору cf значення біта, який вийшов.

[1]

Бітовий зсув