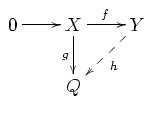|
Ін'єктивний модуль — один з типів модулів, що є двоїстим до проєктивного модуля і широко використовується в гомологічній алгебрі і загалом в теорії кілець.
Означення
Модуль  над кільцем над кільцем  (як правило, вважається асоціативним з одиничним елементом) називається ін'єктивним, якщо для будь-якого гомоморфізма (як правило, вважається асоціативним з одиничним елементом) називається ін'єктивним, якщо для будь-якого гомоморфізма  і мономорфізма і мономорфізма  існує такий гомоморфізм існує такий гомоморфізм  , що , що  , тобто дана діаграма є комутативною: , тобто дана діаграма є комутативною:
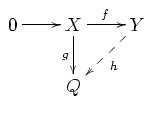
Існує декілька еквівалентних означень:
 - індукована послідовність
 - теж є точною;
 - розщеплюється, тобто підмодуль
 є в М прямим доданком; є в М прямим доданком;
- Модуль
 є прямим доданком у будь-якому модулі в якому він є підмодулем; є прямим доданком у будь-якому модулі в якому він є підмодулем;
- Для будь-якого ідеала (правого для правих модулів, лівого для лівих)
 кільця кільця  будь-який гомоморфізм будь-який гомоморфізм  -модулів -модулів  може бути продовжений до гомоморфізма може бути продовжений до гомоморфізма  -модулів -модулів  Дане означення називається критерієм Бера. У випадку комутативного нетерового кільця, критерій Бера достатньо перевірити для простих ідеалів. Дане означення називається критерієм Бера. У випадку комутативного нетерового кільця, критерій Бера достатньо перевірити для простих ідеалів.
- Для всіх R-модулів T функтор Ext задовольняє умову
 (і тому (і тому  ) )
В термінах теорії категорій можна дати визначення, що  є ін'єктивним об'єктом категорії є ін'єктивним об'єктом категорії  -модулів. -модулів.
Приклади
- Нульовий модуль {0} є ін'єктивним.
- Для будь-якого поля k, довільний k-векторний простір Q є ін'єктивним k-модулем. Дійсно, якщо Q є підпростором простору V, то базис простору Q можна доповнити до базису простору V (наприклад, згідно леми Стейніца про заміну). Якщо K — лінійна оболонка векторів, що доповнюють базис Q до базиса V, то V є прямою сумою підпросторів Q і K, тобто Q є прямим доданком у кожному просторі підпростором якого він є
- Раціональні числа Q (з операцією додавання) утворюють ін'єктивну абелеву групу (тобто Z-модуль). Фактор-група Q/Z теж є ін'єктивним Z-модулем. Фактор-група Z/nZ для n > 1 є ін'єктивною як Z/nZ-модуль, але не ін'єктивною як абелева група.
- ля будь-якої області цілісності R з полем часток K, R-модуль K і ін'єктивним R-модулем, до того ж найменшим ін'єктивним R-модулем, що містить R.
- Для кілець Дедекінда, фактор-модуль K/R теж є ін'єктивним, і його незвідні прямі доданки є локалізаціями
 для ненульових простих ідеалів для ненульових простих ідеалів  . Нульовий ідеал теж є простим і відповідає ін'єктивному модулю K. Тобто існує бієкція між простими ідеалами і незвідними ін'єктивними модулями над кільцем Дедекінда. . Нульовий ідеал теж є простим і відповідає ін'єктивному модулю K. Тобто існує бієкція між простими ідеалами і незвідними ін'єктивними модулями над кільцем Дедекінда.
Властивості
- Кожен R-модуль М можна вкласти в ін'єктивний модуль. Більш того, кожен модуль М міститься в своїй ін'єктивній оболонці Q (M), тобто в ін'єктивному модулі Q (M), кожен ненульовий підмодуль якого має ненульовий перетин з М. Будь-яке вкладення модуля М в ін'єктивний модуль Q продовжується до вкладення ін'єктивної оболонки Q (M) в Q .
- Кожен R-модуль М має ін'єктивну резольвенту, тобто точну послідовність
 в якій всі модулі в якій всі модулі  є ін'єктивними. Довжина найкоротшої ін'єктивної резольвенти називається ін'єктивною розмірністю модуля. Довжиною тут називається число n, таке що є ін'єктивними. Довжина найкоротшої ін'єктивної резольвенти називається ін'єктивною розмірністю модуля. Довжиною тут називається число n, таке що  Якщо такого числа не існує ін'єктивна розмірність вважається нескінченною. Ін'єктивна розмірність ін'єктивних модулів і тільки їх рівна нулю. Якщо такого числа не існує ін'єктивна розмірність вважається нескінченною. Ін'єктивна розмірність ін'єктивних модулів і тільки їх рівна нулю.
- Прямий добуток ін'єктивних модулів є ін'єктивним модулем. Навпаки, якщо прямий добуток модулів є ін'єктивним модулем то й кожен множник теж є ін'єктивним модулем.
- Ін'єктивний модуль Q дорівнює rQ для будь-якого елемента
 , що не є правим дільником нуля в R, тобто ін'єктивний модуль є подільним модулем. Зокрема, абелева група є ін'єктивним модулем над кільцем , що не є правим дільником нуля в R, тобто ін'єктивний модуль є подільним модулем. Зокрема, абелева група є ін'єктивним модулем над кільцем  тоді і тільки тоді, коли вона подільна. тоді і тільки тоді, коли вона подільна.
- Над комутативним нетеровим кільцем R кожен ін'єктивний модуль є прямою сумою ін'єктивних оболонок модулів виду
 , де , де  — простий ідеал кільця R — простий ідеал кільця R
- Всі (ліві і праві) модулі над кільцем R є ін'єктивними тоді і тільки тоді коли кільце є напівпростим.
- Кільце R є нетеровим зліва (справа) тоді і тільки тоді коли пряма сума довільної множини ін'єктивних лівих (правих) R-модулів є ін'єктивним лівим (правим) R-модулем. Іншою еквівалентною умовою є те, що довільний лівий (правий) R-модуль розкладається на пряму суму незвідних лівих (правих) R-модулів.
- Кільце R є артіновим зліва (справа) тоді і тільки тоді кожен ін'єктивний модуль є прямою сумою ін'єктивних оболонок простих модулів. В цьому випадку існує бієкція між простими ідеалами кільця і незвідними ін'єктивними модулями. Кожен простий ідеал в цьому випадку є анігілятором деякого (однозначно визначеного) простого модуля і відповідний незвідний ін'єктивний модуль є його ін'єктивною оболонкою. Для кільця всі підмодулі усіх ін'єктивних модулів є теж ін'єктивними тоді і тільки тоді коли кільце є артіновим напівпростим.
- Кільце є спадковим (тобто кожен ідеал є проективним модулем) якщо і тільки якщо для кожного ін'єктивного модуля над ним всі фактор-модулі теж є ін'єктивними. Іншою еквівалентною умовою є те, що сума двох ін'єктивних підмодулів у довільному модулі теж буде ін'єктивним модулем.
- Якщо кільце R є спадковим зліва (справа) і нетеровим зліва (справа), то кожен R-модуль містить найбільший ін'єктивний підмодуль.
- Проективність (ін'єктивність) всіх ін'єктивних (проективних) R-модулів еквівалентна тому, що R є квазіфробеніусовим кільцем.
- Для довільного R-модуля можна визначити модуль
 Тоді модуль M є плоским тоді і тільки тоді коли M* є ін'єктивним. Для нетерових кілець також навпаки модуль M є ін'єктивним тоді і тільки тоді коли M* є плоским. Тоді модуль M є плоским тоді і тільки тоді коли M* є ін'єктивним. Для нетерових кілець також навпаки модуль M є ін'єктивним тоді і тільки тоді коли M* є плоским.
Див. також
Література
- Картан А., Эйленберг С, Гомологическая алгебра, пер. с англ., М., 1960;
- Маклейн С, Гомология, пер. с англ., М., 1966;
- Faith С, Lectures on infective modules and quotient rings, B.—Hdlb.—N.Y., 1967;
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR 1653294
- Sharpe D. W., Vamos P., Injective modules, Cambridge, 1972.
|