สัญกรณ์โอใหญ่

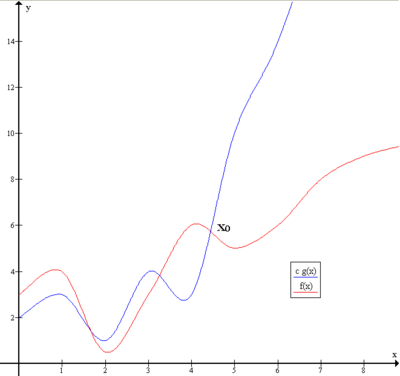
ตัวอย่างของสัญกรณ์โอใหญ่ โดย f(x) ∈ O(g(x)) ซึ่งหมายความว่ามี c > 0 (เช่น c = 1) และ x₀ (เช่น x₀ = 5) ที่ทำให้ f(x) < cg(x) เมื่อ x > x₀

ในวิชาทฤษฎีความซับซ้อนและคณิตศาสตร์ สัญกรณ์โอใหญ่ (อังกฤษ: Big O notation) เป็นสัญกรณ์คณิตศาสตร์ที่ใช้บรรยายพฤติกรรมเชิงเส้นกำกับของฟังก์ชัน โดยระบุเป็นขนาด (magnitude) ของฟังก์ชันในพจน์ของฟังก์ชันอื่นที่โดยทั่วไปซับซ้อนน้อยกว่า สัญกรณ์โอใหญ่เป็นหนึ่งในสัญกรณ์เชิงเส้นกำกับ หรืออาจเรียกว่า สัญกรณ์ของลันเดา หรือ สัญกรณ์ของบัคแมนน์-ลันเดา (ตั้งชื่อตามเอ็ดมุนด์ ลานเดาและเพาล์ บาคมันน์) สัญกรณ์โอใหญ่ใช้ในการเขียนเพื่อประมาณพจน์ในคณิตศาสตร์ ประยุกต์ใช้ในวิทยาการคอมพิวเตอร์เพื่อใช้อธิบายความเร็วประมาณในการทำงานของโปรแกรมในกรณีต้องประมวลผลข้อมูลจำนวนมาก และใช้เพื่ออธิบายประสิทธิภาพของขั้นตอนวิธีหรือโครงสร้างข้อมูลนั้น ๆ

สัญกรณ์โอใหญ่ระบุลักษณะของฟังก์ชันตามอัตราการเติบโต ถึงแม้ฟังก์ชันจะต่างกัน แต่ถ้ามีอัตราการเติบโตเท่ากันก็จะมีสัญกรณ์โอใหญ่เท่ากัน สำหรับสัญกรณ์โอใหญ่แล้ว จะพิจารณาเฉพาะขอบเขตบนของอัตราการเติบโตของฟังก์ชัน อาทิฟังก์ชัน ${\displaystyle n^{2}+n}$ และ ${\displaystyle n+4}$ ล้วนมีอัตราการเติบโตน้อยกว่าหรือเท่ากับ ${\displaystyle n^{2}}$ นั่นคืออัตราการเติบโตของฟังก์ชัน ${\displaystyle n^{2}}$ เป็นขอบเขตบนของ ${\displaystyle n^{2}+n}$ และ ${\displaystyle n+4}$ จึงอาจกล่าวได้ว่า ${\displaystyle n^{2}+n}$ และ ${\displaystyle n+4}$ เป็นสมาชิกของเซตของฟังก์ชัน ${\displaystyle O(n^{2})}$ ในขณะที่สัญกรณ์เชิงเส้นกำกับอื่น พิจารณาขอบเขตอื่น ๆ เช่นสัญกรณ์โอเมกาใหญ่พิจารณาขอบเขตล่างของอัตราการเติบโตของฟังก์ชันแทน

ประวัติ

แนวคิดของสัญกรณ์โอใหญ่ถูกคิดโดยนักทฤษฎีจำนวนที่ชื่อเพาล์ บาคมันน์ (Paul Bachmann) จากงานตีพิมพ์ของเขาที่ชื่อว่า Analytische Zahlentheorie (ทฤษฎีจำนวนวิเคราะห์) ในปี 1894 โดยครั้งนั้นยังไม่ได้ใช้ตัวสัญกรณ์โอใหญ่ สำหรับตัวสัญกรณ์โอใหญ่เองได้รับการใช้อย่างแพร่หลายโดยนักทฤษฎีจำนวนชาวเยอรมัน ที่มีชื่อว่า เอ็ดมุนด์ ลานเดา (Edmund Landau) ชื่อของเขาบางครั้งได้รับการยกย่องให้เป็นชื่อของสัญกรณ์โอใหญ่ว่าเป็น สัญกรณ์ของลานเดา (Landau notation) หรือ สัญกรณ์แบชมาน-ลานเดา (Bachmann-Landau notation) สำหรับตัวสัญกรณ์ที่เขียนเป็นรูปโอใหญ่นั้นได้แนวคิดมาจากคำว่า "order of" ซึ่งเดิมทีนั้นเขียนโดยใช้เป็นโอไมครอนใหญ่

นิยาม

อัตราการเติบโตของฟังก์ชันใด ๆ มีค่าเป็นสัญกรณ์โอใหญ่ของอีกฟังก์ชันหนึ่งแล้ว แสดงว่าอัตราการเติบโตของฟังก์ชันใด ๆ นั้นจะ โตน้อยกว่าหรือเท่ากับ อัตราการเติบโตของฟังก์ชันดังกล่าว ดังนั้นจึงอาจนิยามได้ว่า

ให้ ${\displaystyle f(n)}$ และ ${\displaystyle g(n)}$ เป็นฟังก์ชันบนจำนวนจริงใด ๆ แล้ว จะกล่าวว่า

${\displaystyle f(n)\in O(g(n))}$ เมื่อ ${\displaystyle n\to \infty }$

ก็ต่อเมื่อมีจำนวนจริง ${\displaystyle c}$ และ ${\displaystyle n_{0}}$ ค่าหนึ่งที่ทำให้ ${\displaystyle |f(n)|\leq c|g(n)|}$ ทุก ๆ ${\displaystyle n\geq n_{0}}$

อย่างไรก็ตาม นิยามนี้จำกัดเฉพาะกรณี ${\displaystyle n\to \infty }$ เท่านั้น ซึ่งไม่เพียงพอต่อการอธิบายในกรณีที่ ${\displaystyle n\to a}$ ดังนั้นจึงอาจใช้นิยามในอีกรูปแบบ ในการขยายไปถึงสัญกรณ์โอใหญ่กณิกนันต์ ซึ่งเป็นพิจารณาอัตราการเติบโตของฟังกชันรอบ ๆ จุด a ใด ๆ

ให้ ${\displaystyle f(x)}$ และ ${\displaystyle g(x)}$ เป็นฟังก์ชันใด ๆ จะกล่าวว่า

${\displaystyle f(x)\in O(g(x))}$ ขณะ x เข้าใกล้ a

ก็ต่อเมื่อ ${\displaystyle \lim _{x\to a}\left|{\frac {f(x)}{g(x)}}\right|\in [0,\infty )}$

การขยายนิยามไปหลายตัวแปร

นิยามทั้งสองรูปแบบสามารถขยายไปหลายตัวแปรได้

ให้ ${\displaystyle f(a_{0},a_{1},\ldots ,a_{n})}$ และ ${\displaystyle g(a_{0},a_{1},\ldots ,a_{n})}$ เป็นฟังก์ชันหลายตัวแปรใด ๆ จะกล่าวได้ว่า

${\displaystyle f(a_{0},a_{1},\ldots ,a_{n})\in O(a_{0},a_{1},\ldots ,a_{n})}$

ก็ต่อเมื่อมีจำนวนจริง ${\displaystyle c}$ และ ${\displaystyle n_{0}}$ ค่าหนึ่งที่ทำให้ ${\displaystyle |f(a_{0},a_{1},\ldots ,a_{n})|\leq c|g(a_{0},a_{1},\ldots ,a_{n})|}$ ทุก ๆ ${\displaystyle a_{0},a_{1},\ldots ,a_{n}\geq n_{0}}$

หรือในอีกนิยามที่พิจารณาอัตราการเติบโตของฟังก์ชันรอบ ๆ พิกัด ${\displaystyle (k_{0},k_{1},\ldots ,k_{n})}$ ใด ๆ ว่า

${\displaystyle f(a_{0},a_{1},\ldots ,a_{n})\in O(g(a_{0},a_{1},\ldots ,a_{n}))}$

ก็ต่อเมื่อ ${\displaystyle \lim _{a_{0},a_{1},\ldots ,a_{n}\to k_{0},k_{1},\ldots ,k_{n}}\left|{\frac {f(a_{0},a_{1},\ldots ,a_{n})}{g(a_{0},a_{1},\ldots ,a_{n})}}\right|\in [0,\infty ).}$

ตัวอย่าง

• ${\displaystyle n^{2}+n\leq 2n^{2}}$ ทุกๆ ${\displaystyle n\geq 1}$ (หาได้จากการแก้อสมการ) เพราะฉะนั้น ${\displaystyle n^{2}+n\in O(n^{2})}$ (${\displaystyle c=2,n_{0}=1}$)
• ${\displaystyle n^{2}+4\leq 2n^{2}}$ ทุกๆ ${\displaystyle n\geq 2}$ (หาได้จากการแก้อสมการ) เพราะฉะนั้น ${\displaystyle n^{2}+4\in O(n^{2})}$ (${\displaystyle c=2,n_{0}=2}$)

หรือ

• ${\displaystyle \lim _{n\to \infty }{\frac {n^{2}+n}{n^{2}}}=1}$ เพราะฉะนั้น ${\displaystyle n^{2}+n\in O(n^{2})}$
• ${\displaystyle \lim _{n\to \infty }{\frac {n^{2}+4}{n^{2}}}=1}$ เพราะฉะนั้น ${\displaystyle n^{2}+n\in O(n^{2})}$

การใช้งาน

สัญกรณ์โอใหญ่มีการใช้ในสองกรณีด้วยกัน ได้แก่ กรณีเส้นกำกับอนันต์ และ กรณีเส้นกำกับกณิกนันต์ ความแตกต่างระหว่างสองกรณีนี้เป็นความแตกต่างในขั้นการประยุกต์ใช้ มิใช่ในขั้นหลักการ อย่างไรก็ตาม นิยามเชิงรูปนัยของ "โอใหญ่" นั้นเหมือนกันในทั้งสองกรณี มีเพียงลิมิตสำหรับอาร์กิวเมนต์ของฟังก์ชันเท่านั้นที่แตกต่างกัน

กรณีเส้นกำกับอนันต์

สัญกรณ์โอใหญ่มีประโยชน์ในการใช้วิเคราะห์ขั้นตอนวิธี เพื่อหาประสิทธิภาพของขั้นตอนวิธี ตัวอย่างเช่น สมมติให้เวลา (หรือจำนวนขั้นตอน) ที่ใช้ในการแก้ปัญหาขนาด n มีฟังก์ชันเป็น ${\displaystyle T(n)=4n^{2}-2n+2}$

เมื่อ n มีค่ามากขึ้น พจน์ n^2 จะใหญ่ขึ้นครอบงำพจน์อื่น ๆ จนกระทั่งเราสามารถละเลยพจน์อื่น ๆ ได้ ยิ่งไปกว่านั้น สัมประสิทธิ์ของแต่ละพจน์จะขึ้นกับรายละเอียดปลีกย่อยของการนำขั้นตอนวิธีไปปฏิบัติ ตลอดจนฮาร์ดแวร์ที่ใช้ในการดำเนินการ ฉะนั้นจึงสามารถละเลยได้เช่นกัน สัญกรณ์โอใหญ่จะเก็บเฉพาะส่วนที่เหลือจากที่ละเลยได้ข้างต้น จึงเขียนได้ว่า

${\displaystyle T(n)\in O(n^{2})}$

และกล่าวได้ว่า ขั้นตอนวิธีดังตัวอย่างนี้มีความซับซ้อนเชิงเวลาเป็นอันดับของ n^2

กรณีเส้นกำกับกณิกนันต์

สัญกรณ์โอใหญ่ยังใช้เพื่อแสดงพจน์ของค่าคลาดเคลื่อนโดยประมาณในฟังก์ชันทางคณิตศาสตร์ ตัวอย่างเช่น

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+{\hbox{O}}(x^{3})\qquad {\hbox{as}}\ x\to 0}$

หมายความว่า เมื่อ x มีค่าเข้าใกล้ศูนย์ ผลต่างของฟังก์ชัน ${\displaystyle e^{x}}$ กับ ${\displaystyle 1+x+x^{2}/2}$ (หรืออาจกล่าวอีกนัยหนึ่งว่าเป็นความคลาดเคลื่อนของสองฟังก์ชันนี้) จะมีอยู่ในสับเซตของ ${\displaystyle O(x^{3})}$ นั่นเอง หรือเขียนเป็นสัญลักษณ์ว่า

${\displaystyle \left|e^{x}-\left(1+x+{\frac {x^{2}}{2}}\right)\right|\in {\hbox{O}}(x^{3})\qquad {\hbox{as}}\ x\to 0}$

คุณสมบัติ

การคูณ

การคูณด้วยค่าคงที่

ให้ k เป็นค่าคงที่ใด ๆ ที่เป็นบวก

${\displaystyle O(k\cdot g)=O(g)}$

${\displaystyle f\in O(g)\Rightarrow k\cdot f\in O(g)}$

การซ้อนสัญกรณ์โอใหญ่

${\displaystyle f(n)\in O(g(n))\implies O(f(n))\subset O(g(n))}$

ให้ h (n) เป็นอีกฟังก์ชันหนึ่ง

${\displaystyle O(f(n))\in O(g(n))\implies O(f(h(n)))\subset O(g(h(n)))}$

สัญกรณ์โอใหญ่มาตรฐานน้อยสุด

ในบางครั้งสัญกรณ์โอใหญ่อาจมีการครอบคลุมมากเกินไป เช่น ${\displaystyle O(n^{2})\subset O(n^{3})}$ เป็นต้น จึงทำให้สำหรับฟังก์ชันใด ๆ อาจอยู่ในเซตของสัญกรณ์โอใหญ่หลายค่า จึงมีการกำหนดรูปแบบฟังก์ชันอย่างง่าย ให้ตอบในรูปสัญกรณ์โอใหญ่มาตรฐานน้อยสุด กล่าวคือตอบในรูปแบบมาตรฐานที่เล็กที่สุด เรามักจะอนุโลมให้ใช้จากสัญลักษณ์เท่ากับ (${\displaystyle =}$) แทนสัญลักษณ์สมาชิก (${\displaystyle \in }$) เมื่อใช้กับรูปสัญกรณ์โอใหญ่มาตรฐานน้อยสุดนี้ เช่น ${\displaystyle n^{2}+4=O(n^{2})}$

ในทางวิทยาการคอมพิวเตอร์ การทำงานที่มีสัญกรณ์โอใหญ่มาตรฐานน้อยสุดมีขนาดยิ่งเล็กเท่าใด แสดงว่าทำงานได้ยิ่งเร็วเท่านั้น

สัญกรณ์โอใหญ่มาตรฐานเรียงจากขนาดเล็กไปใหญ่ (ขนาดเล็กหมายถึงจะเป็นซับเซตของขนาดที่ใหญ่กว่า) ให้ m เป็นค่าคงที่ใด ๆ ที่มากกว่าศูนย์ และ n เป็นโดเมนของฟังก์ชัน

สัญกรณ์โอใหญ่มาตรฐาน	ชื่อฟังก์ชัน	หมายเหตุ
${\displaystyle O(1)}$	ค่าคงที่	ไม่ใช้ค่าคงที่อื่นในการแสดงสัญกรณ์ เช่นไม่มีการใช้ O (2)
${\displaystyle O(\log n)}$	ลอการิทึม	ลอการิทึมทุกฐานอยู่ในระดับเดียวกัน เพราะเปลี่ยนฐานได้โดยคูณค่าคงที่
${\displaystyle O(k^{n})}$ 0<k<1	เอกซ์โพเนนเชียลฐานเศษส่วนแท้	ยิ่งค่าฐานมากยิ่งใหญ่
${\displaystyle O((\log n)^{m})}$	โพลีลอการิทึม	ยิ่งเลขชี้กำลังมากระดับยิ่งใหญ่
${\displaystyle O(n^{k}),0<k<1}$	ยกกำลังที่เป็นเศษส่วนแท้ (ติดราก)	ยิ่งเลขชี้กำลังมากระดับยิ่งใหญ่
${\displaystyle O(n)}$	เชิงเส้น	จริง ๆ แล้วเป็นพหุนามรูปแบบหนึ่ง แยกมาเรียกเพราะใช้บ่อย
${\displaystyle O(n^{k}),k>1}$	พหุนาม	ยิ่งเลขชี้กำลังมากระดับยิ่งใหญ่
${\displaystyle O(k^{n})}$ k>1	เอกซ์โพเนนเชียล	ยิ่งค่าฐานมากยิ่งใหญ่
${\displaystyle O(n!)}$	แฟกทอเรียล	อาจรวมถึงการเรียงลำดับสับเปลี่ยน (permutation)
${\displaystyle O(n^{n})}$	n ยกกำลัง n	มีบางครั้งคนใช้ O (n^n) แทน O (n!) แต่ที่จริง O (n^n) ใหญ่กว่า O (n!) เล็กน้อย

บางครั้งเราจำเป็นต้องใช้การผสมโดยการคูณเช่น ${\displaystyle O(nlogn)}$ เกิดจากการคูณระหว่างเชิงเส้นและลอการิทึมย่อมทำได้

สัญกรณ์อื่น