|
Mätbarhet Mätbarheten är ett matematiskt begrepp inom måtteori. Man kan definiera mätbarheten för till exempel mängder, funktioner och predikat. Mätbara mängder
Mätbara mängder är medlemmarna i en sigma-algebra. Mer precist, om är en mängd och är en sigma-algebra i X så kallas paret ett mätbart rum och mängderna mätbara mängder. Detta är den grundläggande definition för mätbarheten eftersom alla andra mätbara begrepp är definierad med hjälp av mätbara mängder. Sigma-algebra är en naturlig selektion för mätbara mängder eftersom det är en uppräknelig konstruktion och uppräknelighet är viktig inom måtteori. TillämpningarMätbara mängder har tillämpningar inom måtteori. Måttrum
Den viktiga tillämpningen för mätbara mängder är måttrummet. Måttrummet är en trippel där är ett mätbart rum och är ett mått. Sannolikhetsrum
En annan tillämpning av mätbara mängder är sannolikhetsrummet. Sannolikhetsrummet är en trippel där är ett mätbart rum och är en sannolikhet. I sannolikhetsrummet kallas mätbara mängder händelser. Vad är naturliga mätbara mängder?Man kunde välja att låta alla mängder vara mätbara eftersom alla mängder bildar en sigma-algebra. Å andra sidan går det alltid att definiera mätbara mängder med avseende på ett mått, som då går att mäta på ett rimligt sätt. Triviala mått, exempelvis Diracmåttet och räknemåttet, är alla mätbara. Därför är de måtten definierade över alla mängder. Å andra sidan, med ett icke-trivialt mått, exempelvis Lebesguemåttet och Hausdorffmåttet, finns det mängder som inte kan tilldelas ett mått. Yttre mått
Ett viktigt exempel på icke-triviala mått är måttet som definieras med hjälp av yttre måttet. Mätbarheten definieras först med Carathéodorys kriterium: om är en mängd och är ett yttre mått definierad i X så är en mängd µ*-mätbar för om Dessa µ*-mätbara mängder är precis de mängder som är mätbara. Man kan visa att en familj är en sigma-algebra, det vill säga en familj av mätbara mängder. Yttre mått är definierade så att yttre mått över µ*-mätbara mängder är ett mått. Mer precist, funktionen är ett mått för dessa mängder. Icke-trivialt exempel: icke-Lebesguemätbara mängder
Lebesguemåttet är definierad med hjälp av Carathéodorys kriterium från yttre Lebesguemåttet och man kallar sedan mätbara mängder Lebesguemätbara. Existensen av mängder i euklidiska rum som inte går att mäta med Lebesguemåttet beror helt på om man accepterar urvalsaxiomet eller inte. Alla bevis som visar på en existens av en icke-mätbar mängd måste använda sig av detta. Idag använder sig alla matematiker av detta axiom, så gott som utan undantag. Urvalsaxiomet innebär att givet en stor samling mängder går det att välja exakt ett element ur var och en av dessa mängder. Det kan tyckas trivialt, men om samlingen är mycket stor får det icke-triviala följder som nämnts ovan. Mätbara funktioner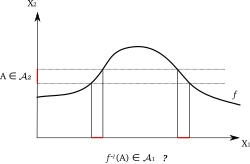
En mätbar funktion är inom matematiken en speciell sorts funktion mellan mätbara rum som bevarar mätbarheten. Formell definitionLåt och vara mätbara rum. En funktion är mätbar om för alla . Man kan också säga att en funktion är -mätbar eller -mätbar. Notera att man inte behöver ha något mått definierat på rummen för att avgöra om en funktion är mätbar. Integration
Motivationen för mätbara funktioner är att man kan "mäta" storleken med måttintegralen. Man definierar måttintegralen med hjälp av mått och mätbara mängder. Mätbara predikat
Ett mätbart predikat är inom matematiken en speciell sorts predikat som definierar en mätbar mängd. Formell definitionLåt vara ett mätbart rum. Ett predikat är mätbar om mängden Nästan överallt
Exempel på mätbara predikat finns nästan överallt. Man kan inte definiera en mätbar mängd utan mätbara predikat. Mätbar sigma-algebra och mätbart måttMan kan även definiera mätbarheten för sigma-algebra och måttet. Låt och vara mätbara rum. Sigma-algebran är mätbar med avseende på sigma-algebran , om
Om är ett mått så är µ mätbart med avseende på om måttets definitionsmängd är mätbar med avseende på . Borelmått
Ett viktigt exempel på mätbart mått är Borelmåttet. Det är ett mått definierat i ett topologiskt rum så att det är mätbart med avseende på Borelmängder. Mer precist, om X är ett topologiskt rum och µ ett mått i X så är måttet µ Borelmåttet om där dom(µ) är µ:s definitionsmängd, det vill säga en sigma-algebra i X. Se även
Källor
|





![{\displaystyle \mu :{\mathcal {F}}\rightarrow [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faceaee8fbc970f5d5862478c7078af9ab71790b)

![{\displaystyle \mathbb {P} :{\mathcal {F}}\rightarrow [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca1cd1636c523d5926754125dfae1ced878d92d4)



















