Cykelindex

Inom kombinatorik är cykelindex ett polynom med flera variabler, vilket är strukturerat så att det sätt på vilket en permutationsgrupp verkar på en mängd enkelt kan utläsas från polynomets koefficienter och exponenter. Detta kompakta sätt att uttrycka information på ett algebraiskt sätt används ofta vid uppräkningar.

Varje permutation π av en ändlig mängd element delar mängden i en eller flera cykliska partitioner. Cykelindexmonomet till π är ett monom av variablerna x₁, x₂, … som beskriver partitionens typ (π:s cykeltyp), där koefficienten anger cykelns längd. Exponenten j i ${\displaystyle x_{k}^{j}}$ anger antalet cykler i π av längden k: exempelvis beskrivs permutationen (1)(28)(37)(46)(5)[1] av monomet ${\displaystyle x_{1}^{2}x_{2}^{3}}$ , d.v.s. att permutationen består av två fixpunkter (partitioner om ett element, vilket avbildas på sig själv) och tre cykliska partitioner om två element. Cykelindexpolynomet för en permutationsgrupp är lika med det aritmetiska medelvärdet av cykelindexmonomen för dess element (d.v.s. för de permutationer som ingår i gruppen).

Om man känner cykelindexpolynomet för en permutationsgrupp kan man räkna upp (enumerera) ekvivalensklasserna som följer av gruppens verkan på mängden. Detta är huvudinnebörden av Pólyas enumerationssats.

Definition

En permutation σ:s cykelindexmonom är monomet

${\displaystyle \prod _{k=1}^{n}x_{k}^{j_{k}(\sigma )}=x_{1}^{j_{1}(\sigma )}x_{2}^{j_{2}(\sigma )}\cdots x_{n}^{j_{n}(\sigma )}}$

där j_k(σ) är hur många cykler av längd k det finns i den fullständiga faktoriseringen av σ.

En permutationsgrupp G:s cykelindexpolynom Z(G) är medelvärdet av cykelindexmonomen av permutationerna i gruppen:

${\displaystyle Z(G)={\frac {1}{|G|}}\sum _{\sigma \in G}\prod _{k=1}^{n}x_{k}^{j_{k}(\sigma )}}$

Följder

Om X är en mängd och permutationsgruppen G är en delgrupp till den symmetriska gruppen över X och p(x₁, ..., x_n) är G:s cykelindexpolynom så kan X färgläggas med q färger, med hänsyn till symmetrierna i G, på p(q, q, ..., q) sätt. Detta är en följd av Burnsides lemma.

En generalisering av detta är Pólyas enumerationssats.

Exempel

En cyklisk grupp med tre element

Ta gruppen C₃ = { e, (1 2 3), (1 3 2)}, som består av identitetsavbildning och två tre-cykler. Cykelindexpolynomet för C₃ är:

${\displaystyle Z(C_{3})={\frac {1}{3}}\left(x_{1}^{3}+2x_{3}\right)}$

Gruppen C₃ kan tolkas som rotationssymmetrierna på en triangel där sidorna är numrerade 1, 2, 3. Om man vill färga triangelns sidor med två färger finns det då

${\displaystyle {\frac {1}{3}}\left(2^{3}+2\cdot 2\right)=4}$

sätt att göra det på. Dessa är att alla sidor har färg 1, alla sidor har färg 2, en sida har färg 1 och de andra färg 2 samt en sida har färg 2 och de andra färg 1.

En dihedral grupp med sex element

De sex spegelsymmetrierna hos en regelbunden sexhörning.

En dihedral grupp med sex element, D₆, motsvarar en regelbunden sexhörnings permutationer under rotation och spegling. Denna har en identitetsavbildning:

${\displaystyle (1)(2)(3)(4)(5)(6)=x_{1}^{6}}$

fem rotationssymmetrier (vridning 60°, 120°, 180°, 240° respektive 300°):

${\displaystyle (123456)=x_{6}(=x_{6}^{1})}$

${\displaystyle (135)(246)=x_{3}^{2}}$

${\displaystyle (14)(25)(36)=x_{2}^{3}}$

${\displaystyle (153)(264)=x_{3}^{2}}$

${\displaystyle (654321)=x_{6}}$

d.v.s. sammanlagt   ${\displaystyle x_{2}^{3}+2x_{3}^{2}+2x_{6}}$

tre speglingar i linjer genom motstående hörn:

${\displaystyle (1)(26)(35)(4)=x_{1}^{2}x_{2}^{2}}$

${\displaystyle (2)(31)(46)(5)=x_{1}^{2}x_{2}^{2}}$

${\displaystyle (3)(42)(51)(6)=x_{1}^{2}x_{2}^{2}}$

d.v.s. sammanlagt   ${\displaystyle 3x_{1}^{2}x_{2}^{2}}$

och tre speglingar i linjer genom motstående sidors mittpunkter:

${\displaystyle (16)(25)(34)=x_{2}^{3}}$

${\displaystyle (21)(36)(45)=x_{2}^{3}}$

${\displaystyle (32)(41)(56)=x_{2}^{3}}$

d.v.s. sammanlagt   ${\displaystyle 3x_{2}^{3}}$

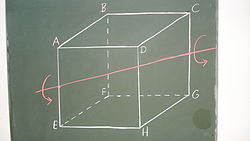
Det aritmetiska medelvärdet av dessa 12 permutationer ger oss:

${\displaystyle Z(D_{6})=(x_{1}^{6}+3x_{1}^{2}x_{2}^{2}+4x_{2}^{3}+2x_{3}^{2}+2x_{6})/12}$

Om vi tänker oss att sexhörningens hörn motsvarar de sex pärlorna på ett fritt[2] halsband och att vi kan välja mellan tre olika sorters pärlor till detta, ger oss Burnsides lemma att det finns

${\displaystyle (3^{6}+3\cdot 3^{2}\cdot 3^{2}+4\cdot 3^{3}+2\cdot 3^{2}+2\cdot 3)/12=92}$

olika sätt att tillverka ett sådant halsband på.

Cykelindex för permutationer av ytorna på en kub

Symmetriaxel genom diagonalt motstående hörn till vänster, och genom diagonalt motstående kanter till höger.

Kub med färgade ytor

Betrakta en vanlig tredimensionell kub och dess symmetriska grupp (automorfismer) och kalla den C. Sym(C) permuterar de sex ytorna på kuben (vi skulle också kunna studera permutationerna av kanter eller hörn). Det finns tjugofyra automorfismer (alla symmetriaxlar går genom kubens centrum):

• En identitet:

Denna permutations bidrag är ${\displaystyle a_{1}^{6}.}$

• Sex 90°-rotationer kring axlar genom motstående sidors mittpunkter:

Tre axlar, en mot- och en medsols rotation per axel. Bidraget är ${\displaystyle 6a_{1}^{2}a_{4}.}$

• Tre 180°-rotationer kring axlar genom motstående sidors mittpunkter:

Samma tre axlar men bara en rotation per axel. Bidraget är ${\displaystyle 3a_{1}^{2}a_{2}^{2}.}$

• Åtta 120°-rotationer kring axlar genom diagonalt motstående hörn (och genom kubens mittpunkt - se figur till höger):

Fyra tretaliga axlar. Två rotationer per axel (det tredje läget är ju identiteten) Bidraget är ${\displaystyle 8a_{3}^{2}.}$

• Sex 180°-rotationer kring axlar genom diagonalt motstående kanters mittpunkter (och kubens mittpunkt - se figur till höger):

Bidrag ${\displaystyle 6a_{2}^{3}.}$

Cykelindex för C blir sålunda:

${\displaystyle Z(C)=(a_{1}^{6}+6a_{1}^{2}a_{4}+3a_{1}^{2}a_{2}^{2}+8a_{3}^{2}+6a_{2}^{3})/24.}$

Har vi k färger till hands kan vi alltså färga kubens sidor på

${\displaystyle (k^{6}+3k^{4}+12k^{3}+8k^{2})/24}$

olika sätt. För k=2 blir antalet sätt 10, för k=3 blir det 57 och har vi exempelvis tio färger blir det 43450.

De tio sätten för två färger (t.ex. svart och vit) är: (1) alla sidor vita, (2) en sida svart (resten är såklart vita), (3) två intilliggande sidor svarta, (4) två motstående sidor svarta, (5) tre svarta sidor som möts i samma hörn, (6) tre svarta sidor varav två är motstående, (7) två vita intilliggande sidor, (8) två motstående vita sidor, (9) en vit sida och (10) alla sidor svarta.

Vid tre färger får man tre enfärgade kuber (trivialt), 3×8=24 kuber med två färger (analogt med de åtta tvåfärgade vid k=2, men nu kan vi bilda tre par) och övriga 30 är trefärgade: De tre respektive färgerna kan fördelas på 1+1+4 (tre olika färger kan användas för de fyra sidorna och de två övriga sidorna kan antingen vara motstående eller intilliggande, d.v.s. 3×2=6 möjligheter), 1+2+3 (3!×3=18 möjligheter: sex möjligheter att fördela färgerna gånger de tre sidorna av samma färg möts i ett hörn + de två sidorna av samma färg är motstående + ingetdera fallet) eller 2+2+2 sidor (alla färger motstående, en färg motstående och inga färger motstående ger 1+3+2=6 möjligheter; den sista tvåan beror på chiralitet).
Fallet med tio färger lämnas åt läsaren.

Cykelindex för olika grupper

Trivialgruppen E_n

Trivialgruppen innehåller endast identitetsavbildningen, sålunda har vi:

${\displaystyle Z(E_{n})=a_{1}^{n}.}$

Den cykliska gruppen C_n

Den cykliska gruppen C_n utgörs av gruppen av rotationer i planet av en regelbunden polygon med n kanter (eller hörn), eller av n objekt jämnt utbredda längs en cirkels omkrets. Den har φ(d) element av ordningen d som delar n. φ(d) är Eulers fi-funktion och ger antalet naturliga tal mindre än d som är relativt prima till d. En permutation av ordningen d har n/d cykler av längden d, sålunda:[3]

${\displaystyle Z(C_{n})={\frac {1}{n}}\sum _{d|n}\varphi (d)a_{d}^{n/d}.}$

Den dihedrala gruppen D_n

Den dihedrala gruppen D_n är en cyklisk grupp med n element som också tillåter spegling:

${\displaystyle Z(D_{n})={\frac {1}{2}}Z(C_{n})+{\begin{cases}{\frac {1}{2}}a_{1}a_{2}^{(n-1)/2},&n{\mbox{ udda, }}\\{\frac {1}{4}}\left(a_{1}^{2}a_{2}^{(n-2)/2}+a_{2}^{n/2}\right),&n{\mbox{ jämnt.}}\end{cases}}}$

Den alternerande gruppen A_n

Den alternerande gruppen A_n utgörs av de jämna permutationerna av på en mängd bestående av n element. Om antalet transpositioner (parvisa byten) av objekten för att åstadkomma en permutation är jämnt är permutationen jämn, annars udda. Exempelvis kan man genom att byta plats på a och b i abcd åstadkomma den udda permutationen bacd och genom att sedan byta plats på a och c får man den jämna bcad. Permutationerna (1)(2)(3)(4), (12)(34), (13)(24), (14)(23), (1)(234), (1)(243), (2)(134), (2)(143), (3)(124), (3)(142), (4)(123) och (4)(132) av fyra objekt är jämna, övriga tolv är udda. A_n består således av n!/2 element och dess cykelindex ges av:

${\displaystyle Z(A_{n})=\sum _{j_{1}+2j_{2}+3j_{3}+\cdots +nj_{n}=n}{\frac {1+(-1)^{j_{2}+j_{4}+\cdots }}{\prod _{k=1}^{n}k^{j_{k}}j_{k}!}}\prod _{k=1}^{n}a_{k}^{j_{k}}.}$

Referenser

• Brualdi, Richard A. (2010), ”14. Pólya Counting”, Introductory Combinatorics (5th), Upper Saddle River, NJ: Prentice Hall, s. 541–575, ISBN 978-0-13-602040-0 

• Cameron, Peter J. (1994), ”15. Enumeration under group action”, Combinatorics:Topics, Techniques, Algorithms, Cambridge: Cambridge University Press, s. 245–256, ISBN 0-521-45761-0 

• Dixon, John D.; Mortimer, Brian (1996), Permutation Groups, New York: Springer, ISBN 0-387-94599-7 

• Perneby, Susanne (2010), En Introduktion till Pólyas Enumerationssats, Självständiga arbeten i matematik 2010 - No 9, Matematiska Institutionen, Stockholms Universitet, Läst: 2014-10-14.

• Roberts, Fred S.; Tesman, Barry (2009), ”8.5 The Cycle Index”, Applied Combinatorics (2nd), Boca Raton: CRC Press, s. 472–479, ISBN 978-1-4200-9982-9 

• Rotman, Joseph (1995). An Introduction to the Theory of Groups. Springer Verlag. ISBN 978-0-387-94285-8 

• Tucker, Alan (1995), ”9.3 The Cycle Index”, Applied Combinatorics (3rd), New York: Wiley, s. 365–371, ISBN 0-471-59504-7 

• van Lint, J.H.; Wilson, R.M. (1992), ”35.Pólya theory of counting”, A Course in Combinatorics, Cambridge: Cambridge University Press, s. 461–474, ISBN 0-521-42260-4 

Noter

1. Cykelnotation. Exemplet visar den permutation av hörnen som blir följden av att man speglar en regelbunden oktagon (åttahörning) i linjen som går genom de två motstående hörnen 1 och 5.
2. D.v.s. ett som tillåter både rotation och spegling.
3. van Lint & Wilson 1992, s. 464, Exempel 35.1.