Benfords lag

Exempel på slumpade tal
som följer Ben- fords lag väl	som kan vara manipulerade	där Benfords lag inte är tillämplig
45 5 4 4890 71 101 16 3701 1249 144 220 202 213 7 35 58 29 11 1040 98	4 27 7037 821 984 54 43 5 301 120 6 312 2 601 7 941 92 2 101 84	118 98 115 96 100 99 120 114 99 117 101 110 121 93 80 88 93 109 96 91
6 av 20, dvs 30%, ettor som förstasiffra	2 av 20, dvs 10%, ettor som förstasiffra	Alla tal i ett litet intervall

Benfords lag beskriver hur olika siffror är fördelade som förstasiffror i statistik. Lagen säger till exempel att siffran 1 bör vara förstasiffra i 30,1% av fallen, siffran 2 i 17,6% av fallen och siffran 9 i 4,6% av fallen i en mycket stor datamängd.

Om en stor datamängd avviker mycket från Benfords lag kan det vara en indikation på att siffrorna kan vara påhittade eller manipulerade. Detta gör lagen praktiskt användbar för kontroll inom många skilda områden. Som exempel är lagen tillämplig vid ekonomisk redovisning, prislistor, antal röster vid omröstningar mellan ett stort antal alternativ, samt folkmängd i städer.

Lagen är tillämplig vid tal som har så stor varians att de kan tillhöra flera olika dekader, till exempel där N-siffriga tal är vanligast, men är ungefär lika vanliga som tal bestående av N+1 siffror och N-1 siffror. Lagen är således inte giltig vid skostorlekar, telefonnummer, postnummer, med mera. Sannolikheterna kan beräknas med ett logaritmiskt uttryck. Lagen gäller oavsett vilken bas man räknar i, men sannolikheterna blir olika för olika baser.

Matematiskt utseende

Benfords lag säger att sannolikheten för att förstasiffran är x i basen 10 (siffrorna 0 till 9) ges av följande formel:

${\displaystyle P(x)=\log _{10}(x+1)-\log _{10}x=\log _{10}(1+{\frac {1}{x}})}$

Om man använder formeln ovan för alla heltal från 1 till 9 får man följande resultat: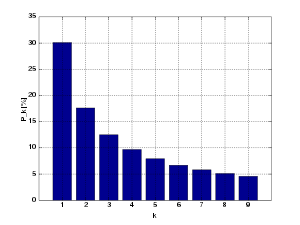

Sannolikhetsfördelningen enligt Benfords lag

x	P
1	30,1%
2	17,6%
3	12,5%
4	9,7%
5	7,9%
6	6,7%
7	5,8%
8	5,1%
9	4,6%

Oberoende av bas

Benfords lag är sådan till naturen att oavsett vilken bas vi använder för att ange våra mätdata i så kommer resultatet att följa Benfords lag. Ett relativt enkelt exempel är att Benfords lag kommer gälla för längden av olika sträckor oavsett vilken enhet vi har valt att mäta dessa sträckor i.

Den allmänna formeln för Benfords lag, alltså formeln i basen b:

${\displaystyle \forall x\in \{1,...,b-1\}\qquad b\geq 2}$

${\displaystyle P(x)=\log _{b}(x+1)-\log _{b}(x)=\log _{b}(1+{\frac {1}{x}})}$

Benfords lag genom åren

Bilden illustrerar Benfords lag

Även om lagen heter Benfords lag så var den förste att uppmärksamma detta fenomen en matematiker vid namn Simon Newcomb, redan 1881 lade han märke till det fenomen som sedan Benford undersökte vidare.[1] Det Newcomb noterade var att logaritmtabeller med låga siffror var mer använda än övriga, han lade som förslag fram den formel som idag kallas Benfords lag.

Näste person att uppmärksamma denna något underliga sannolikhetsfördelning var fysikern Frank Benford. 60 år senare, 1938, visade han resultatet av en undersökning där han hade samlat listor såsom sportresultat, prislistor m.m. innehållande 20 229 olika tal. Han fann att nästan vart tredje tal började med siffran 1, mindre än vart femte tal började med siffran 2, och färre än en tjugondel av siffrorna började med siffran 9.[2] Benfords resultat visade att Newcomb hade haft rätt i sitt antagande angående formelns utseende.

Man bör notera att varken Newcomb eller Benford bevisade de resultat de upptäckt, Benford nöjde sig med att visa att hans lag stämde för ett stort antal undersökningar. Den amerikanske matematikern Theodore Hill har bevisat Benfords lag för vissa "grupper" av statistiska siffror.

Användningsområden för Benfords lag

En logaritmisk skala. För slumpvis utvalda x längs linjen, kommer ungefär 30% av talen att börja med siffran 1 (det bredaste bandet för varje tiopotens).

Hal Varian föreslog 1972 att Benfords lag skulle kunna användas för att upptäcka skattefusk. Om man undersöker siffrorna i skattedeklarationer med mera bör man se att dessa följer Benfords lag, genom att jämföra de faktiska resultaten man får från deklarationerna med den sannolikhetsfördelning som Benfords lag visar bör gälla kan man således upptäcka eventuella skattefuskare. Detta bygger givetvis på att en skattefuskare hittar på siffror helt på måfå och att siffrorna i hans deklaration eller liknande därför har en annan stokastisk fördelning än Benfords fördelning.

Begränsningar för Benfords lag

Benfords lag gäller i många fall men det finns vissa gånger som den inte gäller. Det krävs nämligen att alla tal finns med som möjliga förstasiffror och att fördelningen av dem i alla fall verkar vara slumpvis, till exempel bör inte skostorlekar följa Benfords lag eftersom skostorlekar med förstasiffrorna 6, 7, 8 och 9 är väldigt sällsynta medan storlekar runt 30 och 40 är betydligt vanligare. På samma sätt fungerar det inte att mäta längden hos människor eftersom de flesta är mellan 1 och 2 meter långa, personer på 30 centimeter eller 3 meter är extremt sällsynta.

Man måste därför vara noga med att de data man utgår ifrån har en stor varians, och inte är begränsade till eller i huvudsak koncentrerade inom enbart en eller två tiopotenser.[3]

Se även

• Zipfs lag

Referenser

Delar av den här artikeln är hämtade från engelskspråkiga wikipedia

Noter

1. Simon Newcomb (28 december 1881). ”Note on the frequency of use of the different digits in natural numbers”. American Journal of Mathematics "4" (1/4): ss. 39–40. doi:10.2307/2369148. http://www.uvm.edu/pdodds/files/papers/others/1881/newcomb1881a.pdf. 
2. Frank Benford, 1938, The law of anomalous numbers, Proc. Am. Philos. Soc., 78:4, sid. 551-572.
3. Tommie W. Singleton, 2011, Understanding and Applying Benford’s Law, ISACA Journal, vol 3.

Källor

• Svensson, Andreas Är tärningen kastad? Trollhättan, Bombadil Publishing (2002) ISBN 978-91-85765-02-7

Externa länkar

• Wikimedia Commons har media som rör Benfords lag.
  Bilder & media