|
Фазовая плоскость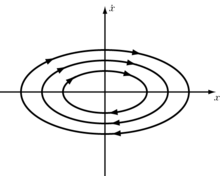 Фа́зовая пло́скость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты), однозначно определяющие состояние системы второго порядка[1]. Фазовая плоскость является частным случаем фазового пространства, которое может иметь бо́льшую размерность. В физике колебаний на оси абсцисс фазовой плоскости откладываются значения параметра x, например, величина отклонения от равновесия; на оси ординат откладываются значения первой производной x по времени — скорости перемещения, что, очевидно, для движущихся материальных тел связывает ось ординат с импульсом тела. См. Фазовое пространство)[2]. Каждая точка фазовой плоскости отражает одно некоторое состояние системы и называется фазовой, изображающей или представляющей точкой[3][4]. Изменение состояния системы отображается на фазовой плоскости движением этой точки. След от движения изображающей точки называется фазовой траекторией. Через каждую точку фазовой плоскости проходит лишь одна фазовая траектория, за исключением особых точек. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность всевозможных различных фазовых траекторий — это фазовый портрет. Он даёт представление о совокупности всех возможных состояний системы и типах возможных движений в ней. Фазовый портрет удобен для рассмотрения движений макроскопических и квантовых частиц[5]. Применение в медицинеФазовая плоскость нашла применение в медицине для повышения достоверности анализа и интерпретации электрокардиограммы (см. Основы фазаграфии[англ.][6]). Метод позволяет одновременно оценивать как амплитудные, так и скоростные параметры элементов кардиосигнала, с высокой точностью оценить форму цикла электрокардиогаммы (ЭКГ) и определить признаки даже самых незначительных патологических изменений в сердце, которые незаметны при традиционной ЭКГ-диагностике[7]. Поскольку дифференцирование зашумлённых функций относится к числу некорректно поставленных математических задач, то для практической реализации фазаграфии привлекаются специальные вычислительные процедуры фильтрации и регуляризации, обеспечивающие надёжную оценку первой производной наблюдаемого ЭКГ-сигнала. Примечания
См. также |