Теорема о шести окружностях

Не следует путать с леммой о шестой окружности.

Примеры конфигураций при изменении радиуса первой окружности. В последнем случае три окружности в цепи совпадают друг с другом.

Теорема о шести окружностях — теорема в геометрии треугольника.

Формулировка

Рассмотрим цепь из окружностей, каждая из которых касается двух сторон данного треугольника, а также предыдущей окружности в цепи. Тогда эта цепь замыкается, в том смысле, что шестая окружность касается первой[1].

Вариации и обобщения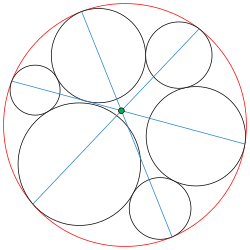

Теорема о семи окружностях

Теорема о семи окружностях

Проведём цепочку из шести черных окружностей (см. рис. справа), каждая из которых касается седьмой окружности (красная) и двух соседних окружностей. Тогда три линии (синие), проведенные между противоположными парами точек касания с седьмой окружностью, пересекаются в одной точке (зеленая). Эта элементарная по сути теорема не была известна вплоть до 1974 года [2][3].

Подобрав радиусы трёх окружностей соответствующим образом (и выставив окружности наружу), можно получить прямые вместо трёх оставшихся окружностей. Эти прямые образуют треугольник, а все четыре нарисованные окружности будут создавать ситуацию с последнего рисунка среди четырёх примеров к основной теореме, где также видны три чевианы к точкам касания окружностей и прямых, пересекающиеся в одной точке.

См. также

• Окружности Мальфатти
• Окружность Форда
• Поризм Штейнера
• Поризм Понселе
• Цепь Паппа Александрийского
• Цепь Понселе
• Лемма о шестой окружности
• Теорема Микеля о шести окружностях
• Теорема о пяти кругах

Примечания

1. Evelyn CJA, Money-Coutts G. B., Tyrrell J. A. The Seven Circles Theorem and Other New Theorems (англ.). — London: Stacey International, 1974. — P. 49—58. — ISBN 978-0-9503304-0-2.
2. Evelyn, C. J. A.; Money-Coutts, G. B.; and Tyrrell, J. A. "The Seven Circles Theorem." §3.1 in The Seven Circles Theorem and Other New Theorems. London: Stacey International, pp. 31-37, 1974.
3. Seven circles theorem. Теорема о шести окружностях (англ. яз.)// https://en.wikipedia.org/wiki/Seven_circles_theorem Архивная копия от 18 мая 2015 на Wayback Machine

Литература

• Wells D. The Penguin Dictionary of Curious and Interesting Geometry (англ.). — New York: Penguin Books, 1991. — P. 231. — ISBN 0-14-011813-6.

Ссылки

• Weisstein, Eric W. Six Circles Theorem (англ.) на сайте Wolfram MathWorld.
• The Six Circle Theorem revisited by D. Ivanov and S. Tabachnikov