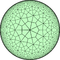
Группа треугольника (2,3,7)

Группа треугольника (2,3,7)[1] — треугольная группа (группа фон Дика) D(2,3,7) сохраняющих ориентацию отображений. Важный объект в теории римановых поверхностей и геометрии Лобачевского в связи с поверхностями Гурвица, а именно^[уточнить] с римановыми поверхностями рода g с максимально высоким возможным порядком группы автоморфизмов, равным 84(g − 1).

Нормальные подгруппы без кручения треугольной группы (2,3,7) являются фуксовыми группами, ассоциированными с поверхностями Гурвица, такими как квартика Клейна^[англ.], поверхность Макбита и первая тройка Гурвица^[англ.].

Построения

Гиперболическое построение

Треугольная группа (2,3,7) является группой сохраняющих ориентацию изометрий мозаик из (2,3,7) треугольников Шварца, показанных здесь в проекции на диск Пуанкаре.

Чтобы построить треугольную группу, начнём с гиперболического треугольника с углами π/2, π/3, π/7. Этот треугольник является наименьшим гиперболическим треугольником Шварца и его отражения замощают плоскость путём отражений относительно сторон. Рассмотрим группу, порождённую отражениями относительно сторон треугольника. Эта группа является неевклидовой кристаллографической группой^[англ.] (дискретной подгруппой гиперболических изометрий) с этим треугольником в качестве фундаментальной области. Ассоциированная мозаика является разделённой семиугольной мозаикой порядка 3^[англ.]. Треугольная группа (2,3,7) определяется как подгруппа индекса 2, состоящая из сохраняющих ориентацию изометрий, и является фуксовой группой (сохраняющей ориентацию неевклидовой кристаллографической группой).

Однородные семиугольные/треугольные мозаики^[англ.]
Симметрия: [7,3], (*732)^[англ.]							[7,3]^+, (732)
{7,3}	t{7,3}^[англ.]	r{7,3}^[англ.]	2t{7,3}^[англ.]=t{3,7}	2r{7,3}^[англ.]={3,7}	rr{7,3}^[англ.]	tr{7,3}^[англ.]	sr{7,3}^[англ.]
Однородные двойственные мозаики
V7^3^[англ.]	V3.14.14	V3.7.3.7	V6.6.7	V3^7	V3.4.7.4	V4.6.14^[англ.]	V3.3.3.3.7

Задание группы

Группа может быть задана при помощи пары генераторов, g₂, g₃, со следующими соотношениями:

${\displaystyle g_{2}^{2}=g_{3}^{3}=(g_{2}g_{3})^{7}=1.}$

Геометрически эти соотношения соответствуют вращениям на 2π/2, 2π/3 и 2π/7 вокруг вершин треугольника Шварца.

Алгебра кватернионов

Группа треугольников (2,3,7) может быть представлена при помощи группы кватернионов с нормой 1 при подходящем R-порядке^[англ.][2] в алгебре кватернионов. Конкретнее, группа треугольника является факторгруппой группы кватернионов по её центру ±1.

Пусть η = 2cos(2π/7). Тогда из равенства

${\displaystyle (2-\eta )^{3}=7(\eta -1)^{2}.}$

видим, что Q(η) является полностью вещественным кубическим расширением Q. Гиперболическая группа треугольника (2,3,7) является подгруппой группы элементов алгебры кватернионов с нормой 1, образованной как ассоциативная алгебра парой генераторов i и j и отношениями i^2 = j^2 = η, ij = −ji. Можно выбрать подходящий порядок кватернионов Гурвица^[англ.] ${\displaystyle {\mathcal {Q}}_{\mathrm {Hur} }}$ в алгебре кватернионов. Здесь порядок ${\displaystyle Q_{\mathrm {Hur} }}$ порождается элементами

${\displaystyle g_{2}={\tfrac {1}{\eta }}ij}$

${\displaystyle g_{3}={\tfrac {1}{2}}(1+(\eta ^{2}-2)j+(3-\eta ^{2})ij).}$

Фактически порядок является свободным Z[η]-модулем над базисом ${\displaystyle 1,g_{2},g_{3},g_{2}g_{3}}$. Генераторы удовлетворяют условиям

${\displaystyle g_{2}^{2}=g_{3}^{3}=(g_{2}g_{3})^{7}=-1,}$

которые сводятся к соотношениям в треугольной группе после взятия факторгруппы по центру.

Связь с SL(2,R)

Визуализация отображения (2,3,∞) → (2,3,7) путём трансформации связанных мозаик[3].

Расширив скаляры из Q(η) в R (путём стандартного вложения), получим изоморфизм между алгеброй кватернионов и алгеброй M(2,R) вещественных 2 х 2 матриц. Выбор конкретного изоморфизма позволяет показать группу треугольника (2,3,7) как частный случай фуксовой группы в SL(2,R), а именно как факторгруппу модулярной группы. Это можно визиуализировать с помощью ассоциированных мозаик, как представлено справа на рисунке — мозаика (2,3,7) диска Пуанкаре является факторпространством модулярной мозаики верхнего полупространства.

Однако для многих целей нет необходимости в явном задании изоморфизма. Так, следы элементов группы (а следовательно, расстояние перемещения гиперболических элементов в верхней полуплоскости, как и систолы фуксовых подгрупп) можно вычислить с помощью сокращённых следов в алгебре кватернионов по формуле

${\displaystyle \operatorname {tr} (\gamma )=2\cosh(\ell _{\gamma }/2).}$

Примечания

1. Под «треугольной группой (2,3,7)» чаще всего понимается не полная треугольная группа Δ(2,3,7) (группа Коксетера с треугольником Шварца (2,3,7), или реализованная как гиперболическая группа отражений^[англ.]), а именно «обычная» треугольная группа ${\displaystyle D(2,3,7)}$.
2. Слово «порядок» многозначно. В данном контексте под порядком понимается порядок кольца (R-порядок). См. книгу Райнера «Максимальные порядки» (Reiner 2003).
3. Platonic tilings of Riemann surfaces: The Modular Group Архивная копия от 28 октября 2009 на Wayback Machine, Gerard Westendorp Архивная копия от 10 марта 2011 на Wayback Machine

Литература

• I. Reiner. Maximum order. — Oxford: Clarendon Press, 2003. — Т. 28 (переиздание). — (London Mathematical Society Monographs New Series).
• N. D. Elkies. Algorithmic Number Theory: Third International Symposium, ANTS-III / Joe P. Buhler. — Springer-Verlag, 1998. — Т. 1423. — (Lecture Notes in Computer Science). — ISBN 3-540-64657-4. — doi:10.1007/BFb0054849.
• M. Katz, M. Schaps, U. Vishne. Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups // J. Differential Geom.. — 2007. — Т. 76, вып. 3. — С. 399–422.