Граф Деджтера

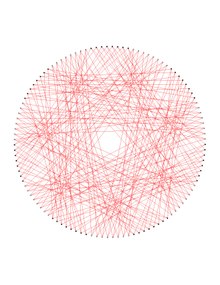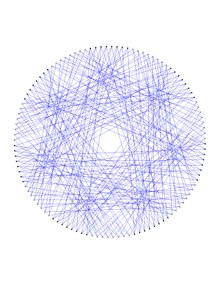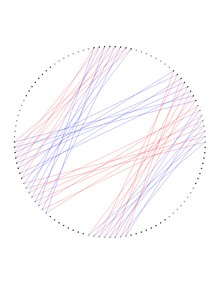Граф Деджтера
Граф Деджтера
Граф Деджтера
Назван в честь Дж. Фолкмана
Вершин 112
Рёбер 336
Радиус 7
Диаметр 7
Обхват 4
Автоморфизмы 2688
Хроматическое число 2
Хроматический индекс 4
Логотип Викисклада Медиафайлы на Викискладе
Красный подграф Любляны
Синий подграф Любляны
Седьмая часть графа Деджтера

Граф Деджтера — это 6-регулярный граф с 112 вершинами, 336 рёбрами и обхватом 4[1][2][3][4][5][6][7]. Граф Деджтера получается путём удаления копии кода Хэмминга длины 7 из бинарного 7-куба.

Описание

Граф Деджтера и любой граф, полученный удалением кода Хэмминга длины 2r-1 из (2r-1)-куба, является симметричным графом (а потому вершинно-транзитивным и рёберно-транзитивным, но не полутранзитивным). В частности, граф Деджтера допускает 3-разложение на две копии графа Любляны, который является третьим по счёту наименьшим рёберно-транзитивным графом, но не вершинно-транзитивным графом регулярной степени 3. Такие графы называются полусимметричными кубическими графами.

Фактически, доказано, что граф Деджтера может быть раскрашен в 2 цвета, скажем, используя набор {красный, синий}, как на верхней фигуре справа, так что оба графа, состоящие из рёбер одного цвета, являются копиями графа Любляны. Эти две копии содержат в точности 112 вершин графа Деджтера и 168 рёбер в каждом, обе копии имеют обхват 10, в то время как граф Деджтера имеет обхват 6, а 7-куб имеет обхват 4. По-видимому, граф Деджтера является наименьшим симметричным графом, имеющим связный самодополнительный стягивающий вершины полусимметричный кубический подграф.

Оба, красный и синий, подграфы Любляны, соединяющие вершины графа Деджтера, могут быть представлены как накрывающие графы графа Хивуда, а именно 8-покрытия графа Хивуда. Это можно получить в каждом из двух представлений графа Любляны (красный сверху, синий ниже, оба справа) путём поочерёдной раскраски последовательных вершин графа Хивуда, скажем, в чёрный и белый (лучше видно при двойном клике на изображение для увеличения размера), поскольку граф Хивуда двудолен. Каждое такое изображение формируется 8 соседями вдоль фиксированной координаты 7-куба, половины кода Хэмминга, имеющего фиксированные веса 0 или 1. При обмене этих весов путём перестановки (0 1) можно перейти от смежности, определённой красным графом Любляны, к смежности, определённой синим графом Любляны и наоборот.

Седьмая часть графа Деджтера показана на отдельном рисунке внизу и она может быть получена из двух получающихся копий графа Хивуда.

Примечания

  1. ↑ Klin, Lauri, Ziv-Av, 2012, с. 1175–1191.
  2. ↑ Borges, Dejter, 1996, с. 161-173.
  3. ↑ Dejter, 1994, с. 55–66.
  4. ↑ Dejter, 1997, с. 301–309.
  5. ↑ Dejter, Guan, 1989, с. 162–174.
  6. ↑ Dejter, Pujol, 1995, с. 18–32.
  7. ↑ Dejter, Weichsel, 1993, с. 67–78.

Литература

  • Klin M., Lauri J., Ziv-Av M. Links between two semisymmetric graphs on 112 vertices through the lens of association schemes // Jour. Symbolic Comput.. — 2012. — Т. 47, вып. 10.
  • Borges J., Dejter I. J. On perfect dominating sets in hypercubes and their complements // J. Combin. Math. Combin. Comput.. — 1996. — Вып. 20.
  • Dejter I. J. On symmetric subgraphs of the 7-cube: an overview // Discrete Math.. — 1994. — Вып. 124.
  • Dejter I. J. Symmetry of factors of the 7-cube Hamming shell // J. Combin. Des.. — 1997. — Вып. 5.
  • Dejter I. J., Guan P. Square-blocking edge subsets in hypercubes and vertex avoidance // Graph theory, combinatorics, algorithms, and applications, SIAM. — San Francisco, CA, 1989.
  • Dejter I. J., Pujol J. Perfect domination and symmetry in hypercubes // Proceedings of the Twenty-sixth Southeastern International Conference on Combinatorics, Graph Theory and Computing. — Boca Raton, Florida, 1995. — Т. 111. — (Congr. Numer.).
  • Dejter I. J., Weichsel P. M. Twisted perfect dominating subgraphs of hypercubes // Proceedings of the Twenty-fourth Southeastern International Conference on Combinatorics, Graph Theory, and Computing (Boca Raton, Florida, 1993).. — 1993.