|
Гипотеза Коллатца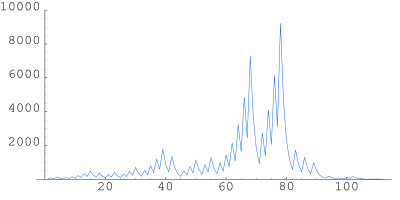 Гипо́теза Ко́ллатца (3n+1 диле́мма, сираку́зская пробле́ма) — одна из нерешённых проблем математики. Получила широкую известность благодаря простоте формулировки. Названа по имени немецкого математика Лотара Коллатца, сформулировавшего похожую задачу 1 июля 1932 года[1]. Формулировка Для объяснения сути гипотезы рассмотрим следующую последовательность чисел, называемую сираку́зской после́довательностью. Берём любое натуральное число n. Если оно чётное, то делим его на 2, а если нечётное, то умножаем на 3 и прибавляем 1 (получаем 3n + 1). Над полученным числом выполняем те же самые действия, и так далее. Гипотеза Коллатца заключается в том, что какое бы начальное число n мы ни взяли, рано или поздно мы получим единицу[2]. ПримерыНапример, для числа 3 получаем:
Последовательность, начинающаяся числом 19, приходит к единице уже за двадцать шагов:
Для числа 27 получаем:
Жирным выделены нечётные числа. Последовательность пришла к единице только через 111 шагов, достигнув в пи́ке значения 9232. Чи́сла-гра́дины — также распространённое название для совокупности рассмотренных последовательностей. Такое название возникло из-за того, что графики последовательностей (см. иллюстрацию) похожи на траектории движения градин в атмосфере. Последовательность первых чисел
Проект «Collatz Conjecture»В августе 2009 года на платформе BOINC был запущен проект добровольных распределённых вычислений «Collatz Conjecture»[3], целью которого является проверка гипотезы Коллатца на больших числах. Вычислительный модуль проекта может использовать вычислительные мощности современных видеокарт. Кроме проекта Collatz Conjecture, с августа 2017 года поиском решения этой проблемы стал также заниматься проект распределённых вычислений yoyo@home[4]. В последние годы проверены все натуральные числа до 3×1020, и каждое из них продемонстрировало соответствие гипотезе Коллатца. Реализация на языках программированияJava: public static ArrayList<Integer> conjectureCollatz (int n) {
//создадим коллекцию для хранения всего ряда чисел
ArrayList<Integer> arrayList = new ArrayList<>();
System.out.println("Исходное значение числа " + n);
//создадим переменную для хранения количества шагов
int stepCount = 0;
while (n != 1) {
//увеличиваем значение счетчика шагов
stepCount++;
//если число четное, то делим на 2
if (n % 2 == 0) {
n /= 2;
//если число нечетное, то умножаем на 3 и прибавляем 1
} else {
n = (n * 3) + 1;
}
//добавляем текущее число в коллекцию
arrayList.add(n);
//выводим текущее значение
System.out.println("На шаге " + stepCount + " значение n равно " + n);
}
//выводим количество шагов алгоритма
System.out.println("stepCount = " + stepCount);
//возвращаем значение коллекции
return arrayList;
}
maxnum = 0
num = int(input("Введите число: "))
while num != 1:
if num % 2 == 0:
num //= 2
else:
num = num*3 + 1
print(num)
maxnum = max(maxnum, num)
print("Пик:", maxnum)
int n;
int i = 0;
Console.WriteLine("Введите число n: ");
n = int.Parse(Console.ReadLine());
while (n != 1) {
if (n % 2 == 0) {
n /= 2;
i += 1;
}
else {
n = 3 * n + 1;
i += 1;
}
}
Console.WriteLine($"{n} {i}");
C++: #include <iostream>
int main() {
int maxnum = 0;
int num = 0;
int count = 0;
std::cin >> num;
while (num != 1) {
if (num % 2 == 0) {
num = num / 2;
} else {
num = num * 3 + 1;
}
std::cout << num << std::endl;
maxnum = std::max(maxnum, num);
count++;
}
std::cout << "Пик: " << maxnum << std::endl;
std::cout << "Шагов: " << count << std::endl;
}
См. также
Примечания
Литература
Ссылки
|
Portal di Ensiklopedia Dunia