Teorema numerelor prime

Teorema numerelor prime descrie distribuția asimptotică a numerelor prime.

În linii mari, teorema precizează că, dacă N este un număr natural suficient de mare, probabilitatea ca un alt număr natural, din vecinătatea lui N să fie prim, este ${\displaystyle {\frac {1}{ln\;N}}}$ , unde ln N este logaritmul natural al lui N. De exemplu, dacă N=10 000, aproximativ unul din 9 sunt prime, iar dacă N=1.000.000.000, numai unul din 21 numere (din vecinătatea lui N) sunt prime.

Enunțul teoremei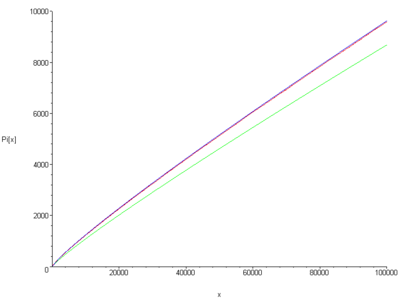

Graficul comparaţiei dintre ${\displaystyle \pi (x)}$   şi   ${\displaystyle {\frac {x}{\ln {x}}}}$.

Se definește „funcția număr prim” ${\displaystyle \pi }$

${\displaystyle \pi (x)=\#\{p\in \mathbb {P} \mid p\leq x\}}$ ,

unde ${\displaystyle x\in \mathbb {R} }$ iar ${\displaystyle \mathbb {P} }$ este mulțimea numerelor prime.

(Simbolul ${\displaystyle \#M}$ reprezintă numărul de elemente sau cardinalul mulțimii M. )

Așadar, ${\displaystyle \pi (x)}$ definește numărul numerelor prime mai mici decât x.

Teorema numerelor prime afirmă că:

${\displaystyle \lim _{x\to \infty }{\frac {\pi (x)}{\frac {x}{\ln(x)}}}=1}$.

Sau, cu alte cuvinte, funcțiile ${\displaystyle \pi (x)}$ și ${\displaystyle {\frac {x}{\ln(x)}}}$ sunt asimptotic echivalente.

Istoric

Teorema numerelor prime demonstrată pentru prima dată de matematicianul francez Jacques Hadamard, în 1896. Teorema a fost demonstrată independent, în același an, și de Charles Jean de la Vallée-Poussin^⁠(en)^[traduceți].

Îmbunătățire a teoremei

Tabel cu π(x), x / ln x și Li(x)

x	π(x)[1]	π(x) - x / lnx	Li(x) - π(x)[2]	x / π(x)
10	4	-0,3	0,921	2,2	2,500
10^2	25	3,3	1,151	5,1	4,000
10^3	168	23	1,161	10	5,952
10^4	1.229	143	1,132	17	8,137
10^5	9.592	906	1,104	38	10,425
10^6	78.498	6.116	1,084	130	12,740
10^7	664.579	44.158	1,071	339	15,047
10^8	5.761.455	332.774	1,061	754	17,357
10^9	50.847.534	2.592.592	1,054	1.701	19,667
10^10	455.052.511	20.758.029	1,048	3.104	21,975

Note

1. „Number of primes < 10^n (A006880)”. On-Line Encyclopedia of Integer Sequences. 
2. „Number of primes < 10^n (A057835)”. On-Line Encyclopedia of Integer Sequences. 

Bibliografie

• Ingham, A.E. - The Distribution of Prime Numbers, Cambridge University, 1990
• Hardy, G.H. - An Introduction to the Theory of Numbers, Oxford University Press, Oxford, 1979

Legături externe

• Tabele cu numere prime Arhivat în 15 noiembrie 2010, la Wayback Machine. de Anton Felkel
• Teorema numerelor prime la MathWorld
• Prime Number Generator Arhivat în 4 septembrie 2009, la Wayback Machine.

Vezi și

• Indicatorul lui Euler