Scădere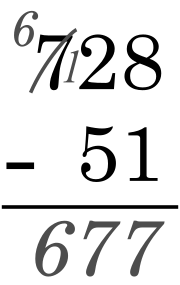

"5 − 2 = 3" (verbal, "cinci minus doi egal 3")

Un exemplu de problemă

Scăderea este una dintre cele 4 operații aritmetice elementare; este inversarea operației de adunare, însemnând că dacă începem cu orice număr la care adăugăm orice număr, apoi scădem numărul pe care l-am adunat, ne întoarcem la numărul cu care am început. Scăderea este reprezentată prin semnul minus.

Denumirile membrilor formulei

c − b = a

sunt descăzut (c) − scăzător (b) = diferență (a).

Scăderea este utilizată pentru patru procese înrudite:

1. Dintr-o mulțime, se înlătură (se scade) un număr cunoscut de elemente. Spre exemplu, din 5 mere minus 2 mere, rămân 3 mere.
2. Dintr-o mărime, se înlătură o valoare numerică exprimată în aceleași unități. Spre exemplu, dacă o persoană cântărind 90 kilograme slăbește 5 kilograme, va cântări 90 − 5 = 85 kilograme.
3. Compararea a două mărimi de același fel pentru a se găsi diferența dintre ele. Spre exemplu, diferența dintre 800 lei și 600 lei este 800 − 600 = 200 lei. Acest proces mai este cunoscut sub numele de scădere comparativă.
4. Pentru a găsi distanța dintre două locuri la o distanță fixă de locul de plecare. Spre exemplu, circulând pe o autostradă, intre o bornă pe care este marcată distanța de 150 kilometri și alta pe care este marcată distanța de 160 kilometri, distanța parcursă între cele două borne este de 160 − 150 = 10 kilometri.

În matematică, deseori este util a vedea sau a defini scăderea ca un tip de adunare. Putem vedea 7 − 3 = 4 ca suma a doi termeni: șapte și minus trei (trei negativ sau opusul lui trei). Această perspectivă permite aplicarea proprietăților și nomenclaturii adunării.

Scăderea nu este asociativă sau comutativă.

Scăderea fundamentală: numere întregi

Fie un segment de dreaptă de lungime b, având capătul stâng notat cu a și cel drept notat cu c. Începând din a, sunt necesari b pași pentru a ajunge în c. Această mișcare spre dreapta este reprezentată matematic prin intermediul adunării:

a + b = c.

Din c, sunt necesari b pași înspre stânga pentru a reveni în punctul a. Această mișcare spre stânga este modelată matematic prin intermediul scăderii:

c − b = a.

Fie un segment de dreaptă notat cu numerele 1, 2 și 3. Din poziția 3, este nevoie de 0 pași pentru a rămâne în poziția 3: 3 − 0 = 0. Sunt necesari 2 pași spre stânga pentru a ajunge pe poziția 1: 3 − 2 = 1. Această imagine nu poate ilustra ce se întâmplă dacă se parcurg cel puțin 3 pași la stânga, începând din poziția 3. Pentru a reprezenta o astfel de operație, segmentul de dreaptă trebuie să fie extins.

Pentru a scădea numere întregi alese arbitrar, se începe cu o semidreaptă care conține toate numerele naturale (0, 1, 2, 3, 4, 5, 6, ...). Din 3, sunt necesari 3 pași pentru a ajunge la 0: 3 − 3 = 0, dar 3 − 4 este din nou o operație ce nu poate fi reprezentată pe segmentul de dreaptă. Pentru a soluționa problema, fie o dreaptă ce conține toate numerele întregi (..., -3, -2, -1, 0, 1, 2, 3, ...). Din 3, sunt necesari 4 pași spre stânga pentru a ajunge în poziția -1: 3 - 4 = -1.