Minimização de circuitos

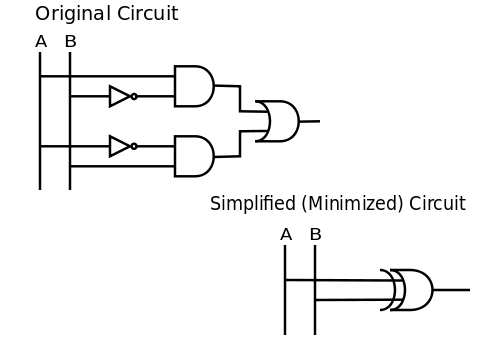
Na álgebra booleana, minimização de circuitos é o problema de se obter o menor circuito lógico, que representa uma função booleana ou uma tabela verdade dada. Acredita-se que o problema de minimização de circuitos é intratável,[1] mas existem heurísticas efetivas como o Mapa de Karnaugh e o algoritmo Quine-McCluskey que facilitam o processo.

Objetivo

O problema de ter um circuito eletrônico complicado (isto é, um com muitos elementos, como as portas lógicas) é que cada elemento ocupa um determinado espaço físico em sua implementação, o que custa tempo e dinheiro para produzi-lo. A minimização de circuitos pode ser uma forma de otimização lógica, usada para reduzir o tamanho da complexidade lógica dos circuitos integrados.

Exemplo

Existem muitas formas de minimizar um circuito, este é um exemplo que minimiza (ou simplifica) uma função booleana. Note que a função booleana realizada pelo circuito está diretamente relacionada com a expressão algébrica da qual a função é implementada.[2] Considere o circuito usado para representar ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)}$. É evidente que duas negações, duas conjunções, e uma dinjunção são utilizadas nessa proposição. Isto significa que para construir o circuito, precisaria-se de duas portas NOT, duas portas AND, e uma porta OR.

Nós podemos simplificar (minimizar) o circuito, aplicando identificadores lógicos ou utilizando a intuição. Uma vez que o exemplo mostra que A é verdadeiro quando B é falso, ou o contrário, podemos concluir que isto simplesmente significa ${\displaystyle A\neq B}$. Em termos de portas lógicas, a desigualdade simplesmente significa uma porta XOR (OU exclusivo). Portanto, ${\displaystyle (A\wedge {\bar {B}})\vee ({\bar {A}}\wedge B)\iff A\neq B}$. Então os dois circuitos mostrados abaixo são equivalentes:

Você pode observar também a veracidade do resultado usando uma tabela verdade.

Ver também

• Árvore de decisão
• Mapa de Karnaugh
• Composição de funções

Referências

1. Kabanets, Valentine; Cai, Jin-Yi (2000), «Circuit minimization problem», Proc. 32nd Symposium on Theory of Computing, Portland, Oregon, USA, pp. 73–79, doi:10.1145/335305.335314, Predefinição:ECCC .
2. M. Mano, C. Kime. "Logic and Computer Design Fundamentals" (Fourth Edition). Pg 54

Leitura adicional

• De Micheli, Giovanni. Synthesis and Optimization of Digital Circuits. McGraw-Hill, 1994, Part III, Logic-Level Syntesis and Optimization
• Zvi Kohavi, Niraj K. Jha. Switching and Finite Automata Theory. 3rd ed. Cambridge University Press. 2009. ISBN 978-0-521-85748-2, chapters 4–6
• Knuth, Donald E. (2010). «chapter 7.1.2: Boolean Evaluation». The Art of Computer Programming. 4A. [S.l.]: Addison-Wesley. pp. 96–133. ISBN 0-201-03804-8