Equação de Helmholtz

A equação de Helmholtz é um tipo de equação diferencial parcial que é expressa da seguinte forma:

${\displaystyle \nabla ^{2}A+k^{2}A=0}$

onde ∇^2 é o Laplaciano, k é o número de onda, e A é a amplitude.

A equação, que recebeu o nome de Hermann von Helmholtz, surge em vários domínios da física e engenharia, tipicamente para descrever fenómenos físicos que são dependentes do tempo. Ela corresponde a um caso geral da Equação de Laplace.

Motivação e usos

A equação de Helmholtz frequentemente surge no estudo de problemas físicos envolvendo equação diferencial parcial (EDP) no espaço e no tempo. A equação de Helmholtz, que representa uma forma independente do tempo da equação de onda, resulta da aplicação da técnica de separação de variáveis para reduzir a complexidade da análise.

Por exemplo, considere a equação de onda $${\displaystyle \left(\nabla ^{2}-{\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}\right)u(\mathbf {r} ,t)=0.}$$

A separação de variáveis começa assumindo que a função de onda u(r, t) é separável: $${\displaystyle u(\mathbf {r} ,t)=A(\mathbf {r} )T(t).}$$

Substituindo esta forma na equação de onda e simplificando, obtemos a seguinte equação: $${\displaystyle {\frac {\nabla ^{2}A}{A}}={\frac {1}{c^{2}T}}{\frac {\mathrm {d} ^{2}T}{\mathrm {d} t^{2}}}.}$$

Note que a expressão do lado esquerdo depende apenas de r, enquanto que a expressão do lado direito depende apenas de t. Como resultado, esta equação é válida no caso geral se, e somente se, ambos os lados da equação forem iguais ao mesmo valor constante. Este argumento é fundamental na técnica de resolver equações diferenciais parciais lineares por separação de variáveis. Desta observação, obtemos duas equações, uma para A(r), e outra para T(t): $${\displaystyle {\frac {\nabla ^{2}A}{A}}=-k^{2}}$$ $${\displaystyle {\frac {1}{c^{2}T}}{\frac {\mathrm {d} ^{2}T}{\mathrm {d} t^{2}}}=-k^{2},}$$

onde escolhemos, sem perda de generalidade, a expressão −k^2 para o valor da constante. (É igualmente válido usar qualquer constante k como constante de separação; −k^2 é escolhida apenas para conveniência nas soluções resultantes.)

Rearranjando a primeira equação, obtemos a equação de Helmholtz (homogénea): $${\displaystyle \nabla ^{2}A+k^{2}A=(\nabla ^{2}+k^{2})A=0.}$$

Da mesma forma, após fazer a substituição ω = kc, onde k é o número de onda e ω é a frequência angular (assumindo um campo monocromático), a segunda equação torna-se

$${\displaystyle {\frac {\mathrm {d} ^{2}T}{\mathrm {d} t^{2}}}+\omega ^{2}T=\left({\frac {\mathrm {d} ^{2}}{\mathrm {d} t^{2}}}+\omega ^{2}\right)T=0.}$$

Agora temos a equação de Helmholtz para a variável espacial r e uma equação diferencial ordinária de segunda ordem no tempo. A solução no tempo será uma combinação linear de funções seno e cosseno, cuja forma exata é determinada pelas condições iniciais, enquanto a forma da solução no espaço dependerá das condições de fronteira. Alternativamente, transformadas integrais, como a Laplace ou transformada de Fourier, são frequentemente usadas para transformar uma equação diferencial parcial hiperbólica numa forma da equação de Helmholtz.

Devido à sua relação com a equação de onda, a equação de Helmholtz surge em problemas em áreas da física como o estudo da radiação eletromagnética, sismologia e acústica.

Resolução da equação de Helmholtz usando separação de variáveis

A solução para a equação de Helmholtz espacial: $${\displaystyle \nabla ^{2}A=-k^{2}A}$$ pode ser obtida para geometrias simples usando a separação de variáveis.

Membrana vibrante

O análogo bidimensional da corda vibrante é a membrana vibrante, com as bordas fixadas para serem imóveis. A equação de Helmholtz foi resolvida para muitas formas básicas no século XIX: a membrana retangular por Siméon Denis Poisson em 1829, o triângulo equilátero por Gabriel Lamé em 1852 e a membrana circular por Alfred Clebsch em 1862. A cabeça de tambor elíptica foi estudada por Émile Mathieu, levando à equação diferencial de Mathieu.

Se as bordas de uma forma são segmentos de linha reta, então uma solução é integrável ou conhecível em forma fechada apenas se for expressável como uma combinação linear finita de ondas planas que satisfazem as condições de fronteira (zero na fronteira, ou seja, membrana fixada).

Se o domínio é um círculo de raio a, então é apropriado introduzir coordenadas polares r e θ. A equação de Helmholtz toma a forma $${\displaystyle A_{rr}+{\frac {1}{r}}A_{r}+{\frac {1}{r^{2}}}A_{\theta \theta }+k^{2}A=0.}$$

Podemos impor a condição de fronteira de que A desaparece se r = a; assim $${\displaystyle A(a,\theta )=0.}$$

A técnica de separação de variáveis leva a soluções de teste da forma $${\displaystyle A(r,\theta )=R(r)\Theta (\theta ),}$$ onde Θ deve ser periódica de período 2π. Isto leva a

$${\displaystyle \Theta ''+n^{2}\Theta =0,}$$ $${\displaystyle r^{2}R''+rR'+r^{2}k^{2}R-n^{2}R=0.}$$

Segue-se da condição de periodicidade que $${\displaystyle \Theta =\alpha \cos n\theta +\beta \sin n\theta ,}$$ e que n deve ser um inteiro. A componente radial R tem a forma $${\displaystyle R(r)=\gamma J_{n}(\rho ),}$$ onde a função de Bessel J_n(ρ) satisfaz a equação de Bessel $${\displaystyle \rho ^{2}J_{n}''+\rho J_{n}'+(\rho ^{2}-n^{2})J_{n}=0,}$$ e ρ = kr. A função radial J_n tem infinitas raízes para cada valor de n, denotadas por ρ_m,n. A condição de fronteira de que A desaparece onde r = a será satisfeita se os números de onda correspondentes forem dados por $${\displaystyle k_{m,n}={\frac {1}{a}}\rho _{m,n}.}$$

A solução geral A então assume a forma de uma série de Fourier generalizada de termos envolvendo produtos de J_n(k_m,nr) e o seno (ou cosseno) de nθ. Estas soluções são os modos de vibração de uma cabeça de tambor circular.

Soluções tridimensionais

Em coordenadas esféricas, a solução é:

$${\displaystyle A(r,\theta ,\varphi )=\sum _{\ell =0}^{\infty }\sum _{m=-\ell }^{\ell }\left(a_{\ell m}j_{\ell }(kr)+b_{\ell m}y_{\ell }(kr)\right)Y_{\ell }^{m}(\theta ,\varphi ).}$$

Esta solução surge da solução espacial da equação de onda e da equação de difusão. Aqui j_ℓ(kr) e y_ℓ(kr) são as funções de Bessel esféricas, e Ym
ℓ(θ, φ) são os harmónicos esféricos (Abramowitz e Stegun, 1964). Note que estas formas são soluções gerais e requerem condições de fronteira para serem usadas em qualquer caso específico. Para domínios exteriores infinitos, uma condição de radiação pode também ser necessária (Sommerfeld, 1949).

Escrevendo r₀ = (x, y, z) a função A(r₀) tem assimptótica

$${\displaystyle A(r_{0})={\frac {e^{ikr_{0}}}{r_{0}}}f\left({\frac {\mathbf {r} _{0}}{r_{0}}},k,u_{0}\right)+o\left({\frac {1}{r_{0}}}\right){\text{ à medida que }}r_{0}\to \infty }$$

onde a função f é chamada amplitude de dispersão e u₀(r₀) é o valor de A em cada ponto da fronteira r₀.

Soluções tridimensionais dada a função num plano bidimensional

Dado um plano bidimensional onde A é conhecido, a solução para a equação de Helmholtz é dada por:[1] $${\displaystyle A(x,y,z)=-{\frac {1}{2\pi }}\iint _{-\infty }^{+\infty }A'(x',y'){\frac {e^{ikr}}{r}}{\frac {z}{r}}\left(ik-{\frac {1}{r}}\right),dx'dy',}$$

onde

${\displaystyle A'(x',y')}$ é a solução no plano bidimensional, ${\displaystyle r={\sqrt {(x-x')^{2}+(y-y')^{2}+z^{2}}},}$ À medida que z se aproxima de zero, todas as contribuições da integral desaparecem exceto para r=0. Assim ${\displaystyle A(x,y,0)=A'(x,y)}$ até um fator numérico, que pode ser verificado como 1 transformando a integral em coordenadas polares ${\displaystyle (\rho ,\theta )}$.

Esta solução é importante na teoria da difração, por exemplo, na derivação da difração de Fresnel.

Aproximação paraxial

Mais informações: Aproximação da envolvente lentamente variável

Na aproximação paraxial da equação de Helmholtz,[2] a amplitude complexa A é expressa como $${\displaystyle A(\mathbf {r} )=u(\mathbf {r} )e^{ikz}}$$ onde u representa a amplitude complexa que modula a onda plana sinusoidal representada pelo fator exponencial. Então, sob uma suposição adequada, u aproximadamente resolve $${\displaystyle \nabla _{\perp }^{2}u+2ik{\frac {\partial u}{\partial z}}=0,}$$ onde ${\textstyle \nabla _{\perp }^{2}{\overset {\text{ def }}{=}}{\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}}$ é a parte transversal do Laplaciano.

Esta equação tem aplicações importantes na ciência da ótica, onde fornece soluções que descrevem a propagação de ondas eletromagnéticas (luz) na forma de ondas parabólicas ou feixes gaussianos. A maioria dos lasers emite feixes que assumem esta forma.

A suposição sob a qual a aproximação paraxial é válida é que a derivada em z da função de amplitude u é uma função lentamente variável de z:

$${\displaystyle \left|{\frac {\partial ^{2}u}{\partial z^{2}}}\right|\ll \left|k{\frac {\partial u}{\partial z}}\right|.}$$

Esta condição é equivalente a dizer que o ângulo θ entre o vetor de onda k e o eixo óptico z é pequeno: θ ≪ 1.

A forma paraxial da equação de Helmholtz é encontrada substituindo a expressão acima para a amplitude complexa na forma geral da equação de Helmholtz como segue:

$${\displaystyle \nabla ^{2}(u\left(x,y,z\right)e^{ikz})+k^{2}u\left(x,y,z\right)e^{ikz}=0.}$$

A expansão e o cancelamento produzem o seguinte:

$${\displaystyle \left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}\right)u(x,y,z)e^{ikz}+\left({\frac {\partial ^{2}}{\partial z^{2}}}u(x,y,z)\right)e^{ikz}+2\left({\frac {\partial }{\partial z}}u(x,y,z)\right)ik{e^{ikz}}=0.}$$

Devido à desigualdade paraxial mencionada acima, o termo ∂^2u/∂z^2 é negligenciado em comparação com o termo k·∂u/∂z. Isto produz a equação de Helmholtz paraxial. Substituindo u(r) = A(r) e^−ikz obtém-se então a equação paraxial para a amplitude complexa original A:

$${\displaystyle \nabla _{\perp }^{2}A+2ik{\frac {\partial A}{\partial z}}=0.}$$

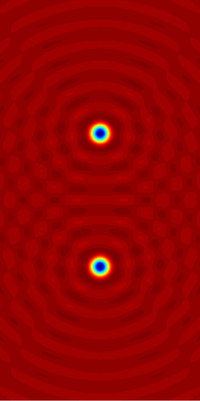
A integral de difração de Fresnel é uma solução exata para a equação de Helmholtz paraxial.[3]

Equação de Helmholtz não homogénea

Duas fontes de radiação no plano, representadas matematicamente por uma função f, que é zero na região azul

A parte real do campo resultante A, A é a solução para a equação de Helmholtz não homogénea (∇^2 + k^2) A = −f.

A equação de Helmholtz não homogénea é a equação $${\displaystyle \nabla ^{2}A(\mathbf {x} )+k^{2}A(\mathbf {x} )=-f(\mathbf {x} )\ {\text{ em }}\mathbb {R} ^{n},}$$ onde ƒ : R^n → C é uma função com suporte compacto, e n = 1, 2, 3. Esta equação é muito semelhante à equação de Poisson com triagem, e seria idêntica se o sinal de mais (na frente do termo k) fosse trocado por um sinal de menos.

Para resolver esta equação de forma única, é necessário especificar uma condição de fronteira no infinito, que é tipicamente a condição de radiação de Sommerfeld

$${\displaystyle \lim _{r\to \infty }r^{\frac {n-1}{2}}\left({\frac {\partial }{\partial r}}-ik\right)A(\mathbf {x} )=0}$$

em ${\displaystyle n}$ dimensões espaciais, para todos os ângulos (ou seja, qualquer valor de ${\displaystyle \theta ,\phi }$). Aqui ${\displaystyle r={\sqrt {\sum _{i=1}^{n}x_{i}^{2}}}}$ onde ${\displaystyle x_{i}}$ são as coordenadas do vetor ${\displaystyle \mathbf {x} }$.

Com esta condição, a solução para a equação de Helmholtz não homogénea é

$${\displaystyle A(\mathbf {x} )=\int _{\mathbb {R} ^{n}}!G(\mathbf {x} ,\mathbf {x'} )f(\mathbf {x'} ),\mathrm {d} \mathbf {x'} }$$

(repare que esta integral é na verdade sobre uma região finita, já que f tem suporte compacto). Aqui, G é a função de Green desta equação, ou seja, a solução para a equação de Helmholtz não homogénea com f igual à função delta de Dirac, então G satisfaz

$${\displaystyle \nabla ^{2}G(\mathbf {x} ,\mathbf {x'} )+k^{2}G(\mathbf {x} ,\mathbf {x'} )=-\delta (\mathbf {x} ,\mathbf {x'} )\in \mathbb {R} ^{n}.}$$

A expressão para a função de Green depende da dimensão n do espaço. Temos $${\displaystyle G(x,x')={\frac {ie^{ik|x-x'|}}{2k}}}$$ para n = 1,

$${\displaystyle G(\mathbf {x} ,\mathbf {x'} )={\frac {i}{4}}H_{0}^{(1)}(k|\mathbf {x} -\mathbf {x'} |)}$$ para n = 2, onde H(1)
0 é uma função de Hankel, e $${\displaystyle G(\mathbf {x} ,\mathbf {x'} )={\frac {e^{ik|\mathbf {x} -\mathbf {x'} |}}{4\pi |\mathbf {x} -\mathbf {x'} |}}}$$ para n = 3. Note que escolhemos a condição de fronteira de que a função de Green é uma onda que se afasta para Predefinição:Mabs → ∞.

Finalmente, para um n geral,

$${\displaystyle G(\mathbf {x} ,\mathbf {x'} )=c_{d}k^{p}{\frac {H_{p}^{(1)}(k|\mathbf {x} -\mathbf {x'} |)}{|\mathbf {x} -\mathbf {x'} |^{p}}}}$$

onde ${\displaystyle p={\frac {n-2}{2}}}$ e ${\displaystyle c_{d}={\frac {1}{2i(2\pi )^{p}}}}$.[4]

Referências

1. Mehrabkhani, S., & Schneider, T. (2017). Is the Rayleigh-Sommerfeld diffraction always an exact reference for high speed diffraction algorithms?. Optics express, 25(24), 30229-30240.
2. J. W. Goodman. Introduction to Fourier Optics 2nd ed. [S.l.: s.n.] pp. 61–62 
3. Grella, R. (1982). «Fresnel propagation and diffraction and paraxial wave equation». Journal of Optics. 13 (6): 367–374. Bibcode:1982JOpt...13..367G. doi:10.1088/0150-536X/13/6/006 
4. Björn Engquist; Hongkai Zhao (November 2018). «Approximate Separability of the Green's Function of the Helmholtz Equation in the High Frequency Limit». Communications on Pure and Applied Mathematics. 71 (11): 2220-2274. doi:10.1002/cpa.21755  Verifique data em: |data= (ajuda)