|
Árvore PatriciaA árvore PATRICIA é uma representação compacta de uma Trie onde os nós que teriam apenas um filho são agrupados nos seus antecessores. É comum que as árvores Trie possuam um grupo disperso de chaves, desse modo, muitos nós possuem apenas um descendente. Isto faz com que as Trie tenham um custo grande de espaço.[1] Uma Trie usa cada uma das partes de uma chave, por vez, para determinar a sub-árvore. Por outro lado, a árvore PATRICIA escolhe um elemento da chave (armazenando a sua posição) para determinar a sub-árvore. Isso remove a necessidade de nós com apenas um descendente. Concebido por Donald Morrison, PATRICIA é um algoritmo para realização de buscas em árvores com as chaves dos nós representadas em binário, sem armazenar as chaves nos nós. O nome é um acrônimo de “Practical Algorithm To Retrieve Information Coded In Alphanumeric”, e o método é particularmente útil para tratamento de chaves de tamanho variável extremamente longas, tais como títulos e frases. No caso de pesquisas analíticas, os dados podem tirar proveito deste método desde que as informações sejam armazenadas como cadeias de texto. Uma restrição dessas árvores é a necessidade de não haver um elemento que seja prefixo de outro, o que pode facilmente ser obtido se necessário. TerminologiaO nome PATRICIA é um acrônimo em inglês para Practical Algorithm to Retrieve Information Coded in Alphanumeric. E é um caso particular da árvore Radix, que é um tipo de árvore de prefixos ou TRIE, em outras palavras, a árvore Patricia é uma árvore Radix binária. HistóriaA árvore PATRICIA foi apresentada pela primeira vez em 1968 por Donald R. Morrison no artigo Practical Algorithm To Retrieve Information Codec In Alphanumeric, publicado no Journal of ACM (sigla para Association for Computing Machinery). A motivação inicial de Morrison foi otimizar a busca de arquivos em bibliotecas.[2] Gernot Gwehenberger independentemente inventou e descreveu a mesma estrutura de dados na mesma época.[3] OperaçõesBuscaA busca por uma string em uma arvore PATRICIA é similar a busca em uma Trie, com a diferença de que ao chegar em um nó, é comparado apenas um caractere, contra a comparação de substrings inteiras que acontece na Trie. No pior caso, a complexidade de tempo é O(|s|), onde s é a string procurada. Inserção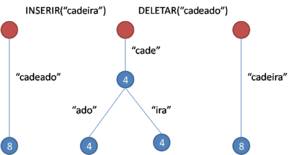 Inserir uma string em uma árvore Patricia é similar a pesquisar por essa string até o ponto onde a busca é encerrada, pois a string não é encontrada na árvore. Se a busca é encerrada em uma aresta, um novo nó é criado nessa aresta. Esse nó armazena a posição do caractere que distingue a chave destino daquela aresta e a chave que se deseja inserir, e tem como filhos o nó que estava na extremidade seguinte da aresta e um novo nó com a parte restante da nova chave. Se a busca for encerrada em um nó, então um nó filho é criado e o restante da nova chave é usado como rótulo para aresta entre os dois. Ambos os casos tem complexidade de tempo de O(|s| + |E|), onde s é a string que será inserida e E é o alfabeto suportado pela árvore. RemoçãoRemover uma string de uma árvore PATRICIA é o oposto da operação de inserção. Primeiro, localiza-se a folha correspondente a string e remove-se ela da árvore. Como o pai terá apenas um filho, os nós pai e irmão do nó removido são agrupados em um único nó. A complexidade de tempo depende diretamente do tempo para remover 2 nós da árvore, se essa remoção for considerada linear, então a complexidade de tempo da operação é O(|s|), onde s é a string que será removida, se essa remoção tiver complexidade O(N), então a complexidade de tempo da operação é O(|s| + N), onde N é o tamanho total de todas as strings armazenadas na árvore. PropriedadesEspaçoUma diferença importante entre a árvore PATRICIA e a árvore Trie é que a árvore PATRICIA não contém nós com apenas um filho. Cada nó tem dois filhos ou é um nó folha. Isso significa que o número de nós internos (não-folha) não ultrapassa o número de nós folhas. Como cada folha corresponde a uma string armazenada pela árvore, então se a árvore tem n strings, a complexidade de espaço é dada por O(n * |E|), onde E é o alfabeto suportado. Além disso, as strings são armazenadas separadamente com complexidade de espaço de O(N), onde N é o tamanho total de todas as strings.[4] Correspondência de PrefixosA árvore PATRICIA possui suporte para uma operação chamada correspondência de prefixos. Essa operação retorna uma lista de todas as strings que possuem uma string especificada como prefixo. Isso é feito pesquisando pela string da mesma forma que a operação de busca até esgotar os caracteres da string. Nesse ponto, cada folha da sub-árvore a partir do nó onde a busca terminou, possui a string procurada como prefixo. A complexidade de tempo para atravessar essa sub-árvore é O(k), onde k é o número de folhas, já que cada nó interno tem, obrigatoriamente, dois filhos. Portanto, a complexidade de tempo dessa operação é O(|s| + k), onde s é a string procurada como prefixo.[4] APLICAÇÕESBanco de DadosO tamanho de uma árvore PATRICIA não depende do tamanho das chaves inseridas nela. Cada nova chave adiciona no máximo um novo nó na árvore. Diferente da árvore-B, a árvore PATRICIA cresce lentamente mesmo com a inserção de um número grande de strings, por causa da alta compressão inerente da estrutura. O ScaleDB é uma estrutura baseada na árvore PATRICIA, porém otimizado para o acesso em disco como a árvore-B.[5] Busca em redes P2PUma questão importante em sistemas P2P é como localizar pontos que contém informação relevante para uma determinada consulta. Para isso, cada ponto capaz de tomar decisões de roteamento precisa manter um índice com os caminhos dos arquivos XML dos vizinhos. Esses índices podem ser eficientemente armazenados em árvores PATRICIA.[6] O problema do maior prefixo comumEncontrar o maior prefixo comum é um problema antigo com diversas aplicações, desde o problema de strings em comum até busca de IP em roteadores de Internet. Com o uso da árvore PATRICIA é possível realizar as funções de Buscarprefixo(x) e Inserir(x) com complexidade de tempo O(log|x|), e Deletar(x) em O(1), onde |x| é o número de bits usados para codificar x. Ou seja, depende apenas de |x| e não do tamanho da estrutura de dados.[7] Ganho de eficiência com documentos XMLA medida em que XML se torna o padrão para troca de informações na Internet, como acessar precisamente dados salvos em arquivos XML aparece como um problema crucial para ser resolvido. A estrutura de indexação usada em XML pode ser substituída por uma estrutura do tipo PATRICIA para ganho de performance em tempo de execução das operações[8] Referências
|
Portal di Ensiklopedia Dunia