|
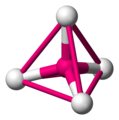
Viervlak
Een viervlak of tetraëder is een veelvlak met vier vlakken in de vorm van een gelijkzijdige driehoek, vier hoekpunten en zes ribben. Het is de 3-simplex en een piramide met een gelijkzijdige driehoek als grondvlak. De oude naam tetraëder komt van het Oudgriekse τετρα, tetra, dat vier betekent en van ἕδρα, hédra, dat stoel of ook zijvlak betekent. Regelmatig veelvlakHet regelmatige viervlak is een van de vijf mogelijke regelmatige veelvlakken en past precies in een kubus, wanneer twee kruisende diagonalen van twee tegenoverliggende zijvlakken van de kubus als twee tegenoverliggende ribben van het viervlak worden genomen. Het regelmatige viervlak is een deltaëder, is zijvlaktransitief en heeft tetrahedrale symmetrie. Er ontstaat een afgeknotte tetraëder door de hoekpunten af te knotten tot een derde deel van de ribben. De vier verwijderde delen zijn dan ook weer een viervlak. KristallografieHet viervlak en het regelmatige achtvlak zijn de twee bouwstenen van de hexagonale dichtste bolstapeling. Er zijn verschillende ruimtevullingen met regelmatige viervlakken mogelijk. Diamant heeft een kubisch vlakgecentreerd rooster met een dubbel aantal atomen, vier regelmatige viervlakken van koolstofatomen per eenheidscel. Alle moleculen met een sp3-hybridisatie, zoals methaan CH4 en siliciumoxide SiO4, hebben de structuur van een viervlak: de koolstof in het middelpunt en de vier waterstofatomen op de vier hoekpunten van het viervlak. Sommige polymeren, meer bepaald de harsen, hebben per monomeer vier reactiepunten, plaatsen waar een verbinding met een andere monomeer mogelijk is. Deze polymeren, bijvoorbeeld bakeliet, vormen een 3D-structuur, opgebouwd uit viervlakken. Afbeeldingen
Formules
Zie de categorie Viervlak van Wikimedia Commons voor mediabestanden over dit onderwerp.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Portal di Ensiklopedia Dunia