Het netwerk links is equivalent met de aansluiting rechts. Volgens de stelling van Thévenin is in een lineair elektrisch netwerk iedere combinatie van spannings - en stroombronnen met weerstanden op twee aansluitpunten elektrisch equivalent aan een spanningsbron met een weerstand in serie . De stelling was eerder in 1853 ontdekt door de Duitse onderzoeker Hermann von Helmholtz , maar werd in 1883 herontdekt door de Franse ingenieur Léon Charles Thévenin (1857-1926).
De grootte van de vervangende spanningsbron en de weerstand worden als volgt bepaald:
De waarde van de spanningsbron is de spanning op de aansluitpunten zonder verbinding.
De vervangende weerstand is de aangesloten stroom gedeeld door de openklemspanning. De stelling wordt samen met de stelling van Norton , de overeenkomstige stelling voor stroombronnen, de elektriciteitswetten van Kirchhoff en de wet van Ohm in de netwerkanalyse toegepast.
Voorbeeld
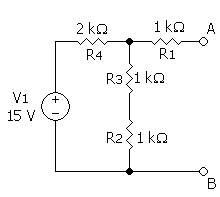
Om het gebruik van de stelling te verduidelijken volgt een voorbeeld. Om de schakeling hieronder te analyseren, bestaat de eerste stap erin om de openklemspanning te bepalen. De volgende stap is om de inwendige weerstand te bepalen. Daaruit volgt het Thévenin-equivalent.
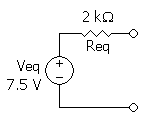
oorspronkelijk netwerk De openklemspanning bedraagt 7,5 V. De inwendige weerstand bedraagt 2 kΩ. het Thévenin-equivalent
Berekening
V
A
B
=
R
2
+
R
3
(
R
2
+
R
3
)
+
R
4
⋅
V
1
{\displaystyle V_{\mathrm {AB} }={R_{2}+R_{3} \over (R_{2}+R_{3})+R_{4}}\cdot V_{\mathrm {1} }}
=
1
k
Ω
+
1
k
Ω
(
1
k
Ω
+
1
k
Ω
)
+
2
k
Ω
⋅
15
V
{\displaystyle ={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \over (1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega )+2\,\mathrm {k} \Omega }\cdot 15\mathrm {V} }
=
1
2
⋅
15
V
=
7
,
5
V
{\displaystyle ={1 \over 2}\cdot 15\mathrm {V} =7,5\mathrm {V} }
R
1
{\displaystyle R_{1}}
A
{\displaystyle A}
B
{\displaystyle B}
R
1
{\displaystyle R_{1}}
R
1
{\displaystyle R_{1}}
De weerstand is:
R
A
B
=
R
1
+
[
(
R
2
+
R
3
)
‖
R
4
]
{\displaystyle R_{\mathrm {AB} }=R_{1}+\left[\left(R_{2}+R_{3}\right)\|R_{4}\right]}
=
1
k
Ω
+
[
(
1
k
Ω
+
1
k
Ω
)
‖
2
k
Ω
]
{\displaystyle =1\ \mathrm {k} \Omega +\left[\left(1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega \right)\|2\ \mathrm {k} \Omega \right]}
=
1
k
Ω
+
(
1
1
k
Ω
+
1
k
Ω
+
1
2
k
Ω
)
−
1
=
2
k
Ω
{\displaystyle =1\ \mathrm {k} \Omega +\left({1 \over 1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega }+{1 \over 2\ \mathrm {k} \Omega }\right)^{-1}=2\ \mathrm {k} \Omega }









![{\displaystyle R_{\mathrm {AB} }=R_{1}+\left[\left(R_{2}+R_{3}\right)\|R_{4}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f117305420c5c21ea1e692ff127cc86dbd958816)
![{\displaystyle =1\ \mathrm {k} \Omega +\left[\left(1\ \mathrm {k} \Omega +1\ \mathrm {k} \Omega \right)\|2\ \mathrm {k} \Omega \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/559ca9be3d5ba4028981fb3d4e7568daf116ed88)
