nl Kristalveldtheorie

Kristalveldtheorie (Engels: crystal field theory; doorgaans afgekort tot CFT) is een model dat de elektronenstructuur van overgangsmetalen in hun verbindingen beschrijft, die doorgaans als metaalcomplexen dan wel coördinatieverbindingen worden bestempeld.^[1]^[2]^[3]^[4]^[5] CFT beschrijft de achtergronden van een aantal (para)magnetische en spectroscopische (kleur) eigenschappen, de hydratatie, enthalpieën, en de structuur van spinel-achtige kristallen. De theorie doet geen uitspraak over de binding die optreedt in de verschillende complexen van overgangsmetalen. CFT is oorspronkelijk ontwikkeld door de fysici Hans Bethe en John Hasbrouck van Vleck^[6] in de jaren '30 van de 20e eeuw. CFT is daarna gecombineerd met de molecuulorbitaaltheorie, waarbij de ligandveldtheorie (LFT) ontwikkeld is. Deze laatste theorie geeft inzicht in het soort bindingen dat optreedt in de complexen van overgangsmetalen.

Overzicht van de kristalveldtheorie

Als basis voor de beschrijving van interactie tussen het ion van het overgangsmetaal en de liganden gebruikt CFT de aantrekkende kracht tussen het positief geladen metaalion en de negatieve lading van een vrij elektronenpaar van het ligand. De theorie beschrijft de energieveranderingen van de vijf ontaarde d-orbitalen ten gevolge van de omringen door een aantal puntladingen bestaande uit de elektronen van de liganden. Als het ligand tijdens de complexvorming het metaalion nadert, zullen de elektronen van het ligand dichter bij sommige van de d-orbitalen komen en verder weg bij andere d-orbitalen. De ontaarding van deze orbitalen vervalt daardoor. Elektronen in de d-orbitalen en die in de ligand stoten elkaar af (gelijke ladingen). De d-elektronen dichter bij de ligand zullen een hogere energie hebben dan de elektronen verder weg, wat resulteert in de splitsing van de energieniveaus van de d-orbitalen. De grootte van de splitsing wordt beïnvloed door de volgende factoren:

het soort metaalion
het oxidatiegetal van het metaalion (een hoger oxidatiegetal geeft een grotere splitsing)
de ruimtelijke verdeling van de liganden rond het metaalion (ruimtelijke structuur)
het soort ligand

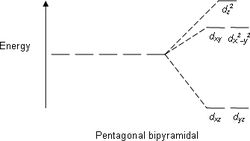
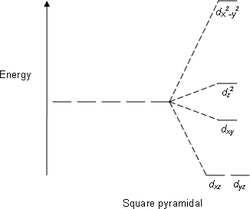
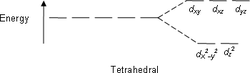
De meeste complexen hebben een octaëdrische omringing: zes liganden vormen een octaëdron rond het metaalion. In octaëdrische omringingen worden de d-orbitalen gesplitst, waarbij het energieverschil beschreven wordt als Δ_oct. De waarde Δ wordt ook aangeduid met de term kristalveld-splitsingsparameter of opsplitsingsenergie. De d_xy-, d_xz- en d_yz-orbitalen krijgen daarbij de lagere energie, d_z²- en de d_x²–y²-orbitalen de hogere energie. De eerste groep is verder weg van de liganden dan de tweede groep en ondervindt dus minder afstoting. De drie lage-energie-orbitalen worden gezamenlijk aangeduid met t_2g, de twee hoge energie-orbitalen als e_g. De namen zijn ontleend aan benamingen uit de moleculaire symmetrie. Voorbeelden van de energie-diagrammen voor de verschillende orbitalen zijn hieronder weergegeven onder het hoofdstuk Hoge-spin en Lage-spin.

De tetraëder vormt de basis voor de tweede grote groep complexen; hier vormen vier liganden een tetraëder rond het metaalion. Ook in een tetraëdrisch kristalveld worden de d-orbitalen in twee groepen gesplitst. Het energieverschil wordt nu aangeduid met Δ_tet, waarbij de orbitalen met de lagere energie gevormd worden door d_z² - en d_x²-y² -orbitalen, de hoge-energiegroep bestaat uit d_xy -, d_xz - en d_yz - orbitalen, dus tegengesteld aan de octaëdergroep. Verder, omdat in de tetraëder-omringing de elektronen van de liganden niet rechtstreeks op de d-orbitalen gericht zijn, is de splitsing kleiner. Andere oriëntaties van liganden, zoals de vlakke vierkant geometrie worden ook goed beschreven door CFT.

Zoals boven al is aangegeven is de grootte van de interactie, dus Δ afhankelijk van de ligand en de geometrie van het complex. Sommige liganden geven altijd kleine waarden voor Δ, andere leiden altijd tot grote waarden van deze parameter. De achtergrond daarvan wordt door de ligandveldtheorie beschreven en verklaard. Daarnaast is er de spectrochemische reeks, een lijst van liganden waarvan de volgorde empirisch is vastgesteld. De volgorde is zodanig dat de liganden die aanleiding geven tot kleine waarden van Δ vooraan staan; liganden die steeds aanleiding geven tot grote waarden van Δ staan achteraan:

I⁻ < Br⁻ < S²⁻ < SCN⁻ < Cl⁻ < NO₃⁻ < N₃⁻ < F⁻ < OH⁻ < C₂O₄²⁻ < H₂O < NCS⁻ < CH₃CN < pyridine < NH₃ < ethyleendiamine < 2,2'-bipyridine < fenantroline < NO₂⁻ < PPh₃ < CN⁻ < CO

Het oxidatiegetal van het metaalion speelt ook een rol in de grootte van Δ, het energieverschil tussen de hoge en de lage energieniveaus. Als het oxidatiegetal groter wordt van een metaalion, neemt de waarde van Δ ook toe. Een V³⁺-complex zal dus een grotere Δ hebben dan het overeenkomstige V²⁺-complex met dezelfde groep liganden. De hogere lading van het V³⁺ heeft tot gevolg dat de liganden sterker worden aangetrokken, de afstand wordt kleiner, en het effect dus groter dan in het V²⁺-ion.

Hoge- en lage-spin-complexen

Liganden die aanleiding geven tot een grote waarde van Δ zoals CN⁻ en CO worden aangeduid als strong-field of sterke veld-liganden. In complexen met deze liganden is het onvoordelig om elektronen in de hoge energiebanen te plaatsen. De lage banen worden zo veel mogelijk opgevuld, waarna eventueel de hogere banen aan de beurt komen (Aufbau principe). De resulterende complexen worden aangeduid met de term low spin-complex. Zo is bijvoorbeeld NO₂⁻ een sterke veld-ligand met een grote waarde van Δ tot gevolg. Het octaëdrische ion [Fe(NO₂)₆]³⁻, met 5 d-elektronen, zal daarom een splitsingspatroon geven zoals hiernaast is weergegeven. De vijf elektronen zitten allemaal in het t_2g niveau.

Andersom worden liganden, zoals I⁻ en Br⁻, die kleine waarden van Δ bij de d-orbitalen veroorzaken aangeduid als weak-field of zwakke veld-liganden. Als deze liganden aan ijzer gebonden zijn wordt het makkelijker gebruik te maken van de hoge energiebanen, omdat dit minder afstoting tussen de elektronen onderling tot gevolg heeft. Het gevolg is dat er eerst in elk van de vijf d-orbitalen een elektron geplaatst wordt (regel van Hund) en een high spin-complex wordt gevormd. Het octaëdrische ion [FeBr₆]³⁻, net als [Fe(NO₂)₆]³⁻, ook met 5 d-elektronen, zal tot een bezetting van alle vijf de orbitalen leiden.

Om de lage-spin toestand te laten optreden moet de energie nodig voor het plaatsen van een elektron in een van de hoge banen, Δ, groter zijn, dan de energie die nodig is om een elektron in een al enkel bezette t_2g orbitaal te plaatsen. De aanduiding e_g verwijst naar d_z² en d_x²-y², die een hogere energie hebben dan de t_2g orbitalen in octaëdrische complexen. Als de energie die nodig is om twee elektronen in één orbitaal te plaatsen groter is dan de energie nodig om een elektron in een e_g te plaatsen, de splitsingsenergie Δ, dan ontstaat een high spin-complex.

Vormen de vier liganden rond het metaalion een tetraëder, dan wordt de splitsingsenergie aangegeven met Δ_tet. De waarde is ongeveer 4/9 × Δ_oct (voor hetzelfde metaal en dezelfde soort liganden). Het gevolg is dat de energie die nodig is om twee elektronen in één baan te zetten, meestal groter is dan de energiekosten voor plaatsing in de hogere baan. Tetraëdrische complexen zijn dan ook bijna allemaal high spin.

De opsplitsingsdiagrammen bieden een goede theoretische verklaring voor de magnetische eigenschappen van de complexen. Een verbinding met ongepaarde elektronen in zijn orbitalen zal paramagnetisch zijn en aangetrokken worden door magneten. Een verbinding waarin alleen gepaarde elektronen voorkomen zal diamagnetisch zijn en licht worden afgestoten door magneten.

Kristalveld-stabilisatie-energie

De kristalveld-stabilisatie-energie (vanuit het Engels: crystal field stabilization energy; vaak afgekort tot CFSE) is de energie die vrijkomt door een overgangsmetaal in een kristalveld van liganden te plaatsen. De stabilisatie ontstaat doordat, als de d-orbitalen gesplitst worden in het ligandveld (zoals hierboven uitgelegd) een aantal een lagere energie krijgen (en andere een hogere) dan voordat de liganden rond het metaalion geplaatst werden, want dan zijn de d-orbitalen gelijk in energie. In de octaëdrische omringing wordt de t_2g set lager in energie dan in het vrije metaalion. Als er elektronen in deze orbitalen voorkomen, zal het complex dus stabieler zijn dan het vrije metaalion. De energiewinst wordt aangeduid met CFSE. Aan de andere kant, de orbitalen in de e_g groep zijn hoger in energie dan die in het vrije ion, dus als elektronen daar geplaatst moeten worden, dan zal de CFSE verlaagd worden.

Als de splitsing van de d-orbitalen in het octaëdrische kristalveld gelijk is aan Δ_oct, dan is de energiewinst voor de drie t_2g orbitalen ²/₅ Δ_oct, en de destabilisatie van de e_g groep gelijk aan ³/₅ Δ_oct. Als voorbeeld gelden de figuren onder de paragraaf over high en low spin-complexen. Het lage-spin (bovenste) voorbeeld heeft vijf elektronen in de t_2g orbitalen, dus is de totale CFSE gelijk aan 5 x ²/₅ Δ_oct = 2Δ_oct. Het hoge-spin (onderste) voorbeeld geeft een CFSE van (3 x ²/₅ Δ_oct) - (2 x ³/₅ Δ_oct) = 0. De energiewinst door de elektronen in de lagere energie-orbitalen wordt tenietgedaan door de extra energie die nodig is om elektronen in de hogere banen te plaatsen.

De redenering rond CFSE is toepasbaar op alle coördinatieverbindingen en complexen met alle mogelijk ruimtelijke verdelingen. Op deze manier kan de veel voorkomende vlakke vierkantverdeling (eigenlijk een octaëdrische omringing met twee vrije elektronenparen) van veel d⁸ complexen verklaard worden door de grote CFSE winst die hier te behalen is.

De kleuren van complexen van overgangsmetalen

De felle kleuren van veel coördinatieverbindingen worden ook verklaard vanuit de kristalveld theorie. Als een d-orbitaal van een dergelijk complex opgesplitst is in 2 niveaus dan kan een dergelijke molecuul bij absorptie van een foton zichtbaar licht direct een of meer elektronen naar de hogere banen laten springen, waarbij een aangeslagen toestand ontstaat. Het energieverschil tussen de grondtoestand en de aangeslagen toestand is gelijk aan de energie van het foton. De fotonenergie is evenredig met de frequentie van de straling, of omgekeerd evenredig met de golflengte ervan. Omdat alleen bepaalde golflengten geabsorbeerd worden laat een oplossing van de stof de complementaire kleur door, de kleur die wij zien.

Zoals boven is uitgelegd, leiden verschillende liganden tot verschillende waarden van Δ, zodat complexen van hetzelfde metaalion verschillende kleuren te zien kunnen geven. Voor een gegeven metaalion zullen de zwakke veld-liganden een complex veroorzaken met een kleine waarde voor Δ, de absorptie zal dan bij langere golflengten optreden, of lagere frequentie ν. Anderzijds zullen de sterke veld-liganden een grote waarde van Δ veroorzaken en dus licht absorberen met een kortere golflengte λ en een hogere ν.

Absorptie versus emissie

De kleurencirkel laat de kleur zien van een verbinding als de verbinding slechts één absorptie in het zichtbare deel van het spectrum vertoont. Als bijvoorbeeld rood licht geabsorbeerd wordt, wordt de verbinding gezien als een groene stof (het groen licht wordt dus geëmitteerd).

λ geabsorbeerd ten opzichte van de kleur van de oplossing:

400 nm: violet geabsorbeerd, groen-geel geëmitteerd (λ = 560 nm)
450 nm: blauw geabsorbeerd, geel geëmitteerd (λ = 600 nm)
490 nm: blauw-groen geabsorbeerd, rood geëmitteerd (λ = 620 nm)
570 nm: geel-groen geabsorbeerd, violet geëmitteerd (λ = 410 nm)
580 nm: geel geabsorbeerd, donkerblauw geëmitteerd (λ = 430 nm)
600 nm: oranje geabsorbeerd, blauw geëmitteerd (λ = 450 nm)
650 nm: rood geabsorbeerd, groen geëmitteerd (λ = 520 nm)

Kristalveld-splitsingspatronen

Splitsingsdiagrammen in een kristalveld
Octaëder Vierzijdige bipiramide	Vijfzijdige bipiramide	Vlak antiprisma

Vlak vierkant	Vierzijdige piramide	Tetraëder

Trigonal bipyramidal Driezijdige bipiramide

Overzicht van geometrieën

Zie ook

Bronnen, noten en/of referenties

↑ Steven S. Zumdahl.957-964.. (2005). GEEN TITEL OPGEGEVEN Chemical Principles Fifth Edition pag.: 550–551 – Houghton Mifflin Company (Boston)
↑ Steven S. Zumdahl. (2005). GEEN TITEL OPGEGEVEN Chemical Principles Fifth Edition pag.: 957–964 – Houghton Mifflin Company (Boston)
↑ Martin S. Silberberg. (2006). GEEN TITEL OPGEGEVEN Chemistry: The Molecular Nature of Matter and Change, Fourth Edition pag.: 1028–1034 – McGraw Hill Company (New York)
↑ D.F. Shriver, P.W. Atkins. (2001). GEEN TITEL OPGEGEVEN Inorganic Chemistry third edition pag.: 227–236 – University Press (Oxford)
↑ G.L. Miessler, D.A. Tarr. (2003). GEEN TITEL OPGEGEVEN Inorganic Chemistry third edition – Pearson Prentice Hall (New Jersey) ISBN 0-13-035471-6
↑ J. H. Van Vleck. (1932). Theory of the Variations in Paramagnetic Anisotropy Among Different Salts of the Iron Group Phys. Rev. 41 pag.: 208–215

[1] Steven S. Zumdahl.957-964.. (2005). GEEN TITEL OPGEGEVEN Chemical Principles Fifth Edition pag.: 550–551 – Houghton Mifflin Company (Boston)

[2] Steven S. Zumdahl. (2005). GEEN TITEL OPGEGEVEN Chemical Principles Fifth Edition pag.: 957–964 – Houghton Mifflin Company (Boston)

[3] Martin S. Silberberg. (2006). GEEN TITEL OPGEGEVEN Chemistry: The Molecular Nature of Matter and Change, Fourth Edition pag.: 1028–1034 – McGraw Hill Company (New York)

[4] D.F. Shriver, P.W. Atkins. (2001). GEEN TITEL OPGEGEVEN Inorganic Chemistry third edition pag.: 227–236 – University Press (Oxford)

[5] G.L. Miessler, D.A. Tarr. (2003). GEEN TITEL OPGEGEVEN Inorganic Chemistry third edition – Pearson Prentice Hall (New Jersey) ISBN 0-13-035471-6

[6] J. H. Van Vleck. (1932). Theory of the Variations in Paramagnetic Anisotropy Among Different Salts of the Iron Group Phys. Rev. 41 pag.: 208–215

[1]

[2]

[3]

[4]

[5]

[6]