|
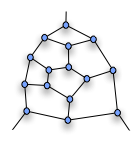
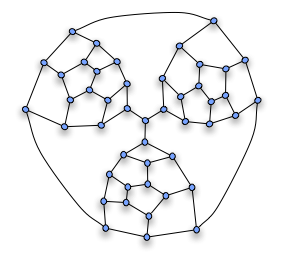
Hamiltonpad  Een hamiltonpad is een pad langs knooppunten in een graaf waarbij elk knooppunt precies één keer op het pad ligt. Een gesloten hamiltonpad noemt men een hamiltoncykel of hamiltoncircuit. De naam hamiltonpad komt van de Ierse wiskundige Sir William Rowan Hamilton (1805-1865). Een graaf die een hamiltoncircuit bevat noemt men een hamiltoniaanse graaf of hamilton-graaf. Elke cykel-graaf is hamiltoniaans, evenals elke volledige graaf met 3 of meer knopen. Een graaf is hamilton-verbonden of hamilton-geconnecteerd als voor elk paar van onderscheiden knooppunten u en v er een hamiltonpad bestaat met als eindpunten u en v. De graaf bestaande uit één enkel knooppunt is triviaal hamilton-verbonden. Het bepalen of er een hamiltonpad of hamiltoncircuit bestaat in een gegeven graaf, die gericht of niet-gericht kan zijn, is een fundamenteel probleem in de grafentheorie. Dit hamiltonpadprobleem is NP-volledig. Het is een speciaal geval van het handelsreizigersprobleem; dat bekomen wordt door de afstand tussen twee steden gelijk aan één te stellen als ze aanliggend zijn, en gelijk aan twee als dat niet zo is. Als de afgelegde afstand gelijk aan het aantal steden is, is de route een hamiltonpad. Als er geen hamiltonpad is, zal de kortste route langer zijn. Het vermoeden van TaitPeter Tait formuleerde in 1884 het volgende vermoeden: "Elke 3-verbonden, planaire, kubische graaf bevat een hamiltoncircuit." (Een kubische graaf is een graaf waarvan elke knoop verbonden is met drie andere knopen; een 3-verbonden graaf is een graaf waaruit minstens 3 knopen moeten verwijderd worden om een niet-samenhangende graaf over te houden). Dit vermoeden werd in 1946 ontkracht door William Tutte,[1] die een tegenvoorbeeld construeerde met 46 knopen en 69 kanten. Hij observeerde dat wanneer een graaf het volgende fragment bevat: elk hamiltoncircuit het fragment moet binnengaan en verlaten via de bovenste knoop en een van de onderste twee; het kan niet langs een van de onderste knopen binnengaan en langs de andere buitengaan en toch het ganse fragment aandoen. Wanneer nu drie van deze fragmenten gecombineerd worden in een graaf als volgt: dan zou een hamiltoncircuit langs de drie kanten rond de centrale knoop moeten passeren, hetgeen onmogelijk is. Holton en McKay[2] bewezen in 1988 dat de kleinste 3-verbonden kubische planaire grafen zonder hamiltoncircuit 38 knopen hebben. Zulke kleinste tegenvoorbeelden van het vermoeden van Tait waren rond 1965 onafhankelijk van elkaar gevonden door Joshua Lederberg, David Barnette en Juray Bosák. Stelling van TutteWilliam Tutte bewees in 1946 dat elke 4-verbonden planaire graaf (met minstens twee kanten) een hamiltoncircuit heeft.[3] Stelling van OreDe stelling van Ore geeft een voldoende voorwaarde opdat een graaf een hamiltonpad heeft, die erop neerkomt dat een graaf met een "voldoend groot aantal kanten" een hamiltonpad heeft. Zie ookBronnen, noten en/of referenties
|
Portal di Ensiklopedia Dunia