| Gamma
|
Kansdichtheid
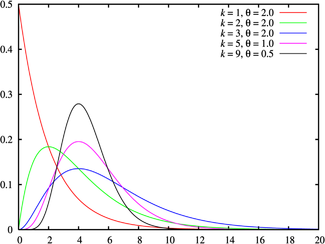
|
Verdelingsfunctie
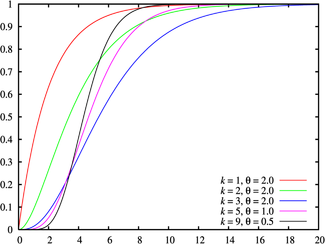
|
| Parameters
|


|
| Drager
|

|
| Kansdichtheid
|

|
| Verdelingsfunctie
|

|
| Verwachtingswaarde
|

|
| Modus
|
 als als 
|
| Variantie
|

|
| Scheefheid
|

|
| Kurtosis
|

|
| Entropie
|


|
Moment-
genererende functie
|
 als als 
|
| Karakteristieke functie
|

|
|
|
In de kansrekening en statistiek is de gamma-verdeling een continue kansverdeling, met twee parameters. De exponentiële verdeling, de chi-kwadraatverdeling en de Erlang-verdeling zijn speciale gevallen van de gamma-verdeling.
Definitie
De kansdichtheid van de gamma-verdeling met vormparameter  en schaalparameter
en schaalparameter  , ook genoteerd als
, ook genoteerd als  -verdeling, is:
-verdeling, is:

waarbij  de gammafunctie is.
de gammafunctie is.
Eigenschappen
- Als
 een
een  -verdeling heeft, dan heeft
-verdeling heeft, dan heeft  een
een  -verdeling, voor willekeurige
-verdeling, voor willekeurige  .
.
- Als
 onderling onafhankelijk en gelijkverdeeld zijn volgens de exponentiële verdeling met parameter
onderling onafhankelijk en gelijkverdeeld zijn volgens de exponentiële verdeling met parameter  , dan heeft
, dan heeft  een
een  -verdeling.
-verdeling.
- De
 -verdeling is de exponentiële verdeling met parameter
-verdeling is de exponentiële verdeling met parameter  .
.
- Als
 een
een  -verdeling heeft, dan heeft
-verdeling heeft, dan heeft  een chi-kwadraatverdeling met
een chi-kwadraatverdeling met  vrijheidsgraden. Daaruit blijkt dat de
vrijheidsgraden. Daaruit blijkt dat de  -verdeling identiek is aan de chi-kwadraatverdeling met
-verdeling identiek is aan de chi-kwadraatverdeling met  vrijheidsgraden.
vrijheidsgraden.
- De
 -verdeling is een Erlang-verdeling met parameters
-verdeling is een Erlang-verdeling met parameters  en
en  . Hierin is
. Hierin is  een reëel en
een reëel en  een geheel getal.
een geheel getal.
Toepassingen
De gamma-verdeling wordt vaak gebruikt wanneer er verschillende, onderling onafhankelijke, experimenten met een exponentiële verdeling in het spel zijn. Stel dat de wachttijd in minuten op de bus bij een halte een exponentiële verdeling met parameter  volgt, dan heeft, onder bepaalde onafhankelijkheidsaannames, de wachttijd op de vijfde bus een
volgt, dan heeft, onder bepaalde onafhankelijkheidsaannames, de wachttijd op de vijfde bus een  -verdeling.
-verdeling.








































