ആരേഖം

ഇംഗ്ലീഷ് വിലാസം

https://ml.wikipedia.org/wiki/Function_of_a_graph

[−2,+3] എന്ന അന്തരാളത്തിലെ വിലകൾ ഇന്പുട് നല്കി കിട്ടുന്ന f(x) = x^4 − 4^x എന്ന ഫലനത്തിന്റെ ആരേഖം.

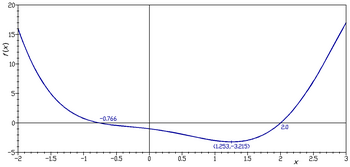ഗണിതത്തിൽ f എന്ന x ന്റെ ഒരു ഫലനം ഉണ്ടെങ്കിൽ, (x, f(x))എന്ന എല്ലാ ക്രമീകൃതജോഡികളുടെയും ഗണമാണ് അതിന്റെ ആരേഖം അഥവാ ഗ്രാഫ്.[1] ഇതിന്റെ ചിത്രീകൃതരൂപത്തെയും അതെ പേരിൽ തന്നെയാണ് വിളിയ്ക്കുന്നത്. x എന്ന ഇന്പുട് ഒരു വാസ്തവികസംഖ്യയാണെങ്കിൽ അതിന്റെ ആരേഖം രണ്ടു മാനങ്ങൾ ഉള്ളതായിരിയ്ക്കും. ഒരു അനുസ്യൂതഫലനത്തിന്റെ ആരേഖം ഒരു വക്രരേഖ ആയിരിയ്ക്കും.

ഒരു ഫലനത്തിന്റെ ആരേഖം എന്ന ആശയത്തെ കൂടുതൽ വിപുലപ്പെടുത്തി ഒരു ബന്ധത്തിന്റെ ആരേഖവും വരയ്ക്കാൻ സാധിയ്ക്കുന്നതാണ്. ഒരു ബന്ധം ഒരു ഫലനം ആണോ എന്ന് നോക്കാനായി ലംബരേഖാ ടെസ്റ്റ് ചെയ്തു നോക്കാവുന്നതാണ്. ഒരു ബന്ധം ഒന്നിലധികം ചരങ്ങളുടെ ഫലനം ആണോ എന്ന് നോക്കാനായി തിരശ്ചീനരേഖാ ടെസ്റ്റ് ചെയ്തും നോക്കാവുന്നതാണ്.. ഒരു ഫലനത്തിന് എതിർഫലനം ഉണ്ടെങ്കിൽ അത് കണ്ടുപിടിയ്ക്കാനായി ഒരു ഗ്രാഫിന്റെ y = x എന്ന രേഖയിലൂടെയുള്ള പ്രതിബിംബം എടുത്താൽ മതി.[1]

സയൻസിലും എഞ്ചിനീറിങ്ങിലും സാങ്കേതികവിദ്യയിലും സാമ്പത്തികശാസ്ത്രത്തിലും മറ്റു പല മേഖലകളിലും ആരേഖങ്ങളുടെ ഉപയാഗം വളരെയേറെയുണ്ട്.ഏറ്റവും ലഘുവായ ഉപയോഗത്തിൽ ഒരു ചരത്തെ മറ്റൊന്നിന്റെ ഫലനമായി രണ്ടു മാനങ്ങളിൽ ആരേഖം വരയ്ക്കുക എന്നുള്ളതാണ്.

ആധുനിക ഗണസിദ്ധാന്തപ്രകാരം വാസ്തവത്തിൽ ഒരു ഫലനവും ആരേഖവും ഒന്നു തന്നെയാണ്.[2] എന്നാൽ ഫലനം എന്ന ആശയം ഗണങ്ങൾ തമ്മിലുള്ള മാപ്പിംഗ് എന്ന ആശയത്തെ കാണിയ്ക്കാനാണ് കൂടുതൽ ഉപയോഗിയ്ക്കുന്നത്. ആരേഖത്തിൽ ഈ മാപ്പിംഗ് അത്രയ്ക്കും വ്യക്തമാകില്ല. അതിനാൽ ഒരു ഫലനത്തെ അതിന്റെ ആരേഖത്തിൽ നിന്നും വേർതിരിച്ച് പഠിയ്ക്കുന്നതാണ് ഫലനങ്ങളെപ്പറ്റി വ്യക്തമായി പഠിയ്ക്കാൻ നല്ലത്. ആരേഖങ്ങളെ ഫലനങ്ങളുടെ ചിത്രീകരണമായി കാണുന്നതാണ് നല്ലത്. ആരേഖം എന്ന ആശയം ഫലനത്തിന്റെ ബീജഗണിതത്തെയും ജ്യാമിതിയെയും ഒന്നിപ്പിയ്ക്കുന്നു.[1]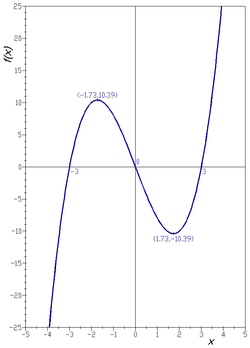

f(x) = x^3 − 9x എന്ന ഫലനത്തിന്റെ ആരേഖം

വരയ്ക്കുന്ന വിധം

ഒരു ആരേഖം വരയ്ക്കാനായി ഉള്ള ഏറ്റവും എളുപ്പമുള്ള വഴി 'ബിന്ദുക്കളെ തമ്മിൽ യോജിപ്പിയ്ക്കുക എന്നുള്ളതാണ്'. ഒരു ഫലനത്തിന്റെ എല്ലാ ഇന്പുട് വിലകളെയും അതിന്റെ ഔട്ട്പുട്ട് വിലകളെയും ഒരു കോ ഓർഡിനേറ്റ് സിസ്റ്റത്തിൽ അടയാളപ്പെടുത്തി അവ തമ്മിൽ രേഖാഖണ്ഡങ്ങൾ വഴി ബന്ധിപ്പിയ്ക്കുന്നതാണ് ഈ രീതി[1]

ലംബരേഖാ ടെസ്റ്റ്

ഒരു ബന്ധം ഒരു ഫലനം ആകുന്നത് ആ ബന്ധത്തിന്റെ മണ്ഡലത്തിലെ ഓരോ വിലയ്ക്കും അതിന്റെ രംഗത്തിൽ ഒരേ ഒരു വില ഉണ്ടാകുമ്പോളാണ്.[1] അതായത് y = f(x) എന്ന x എന്ന ബന്ധത്തിൽ x'ന്റെ ഓരോ വിലയ്ക്കും ഓരോ വ്യത്യസ്ത y ഉണ്ടാകുമ്പോൾ. ഒരു ആരേഖത്തിൽ ഇത് കണ്ടുപിടിയ്ക്കാനായി ഏതെങ്കിലും ലംബരേഖ ബന്ധത്തിന്റെ ആരേഖത്തെ ഒന്നിലധികം ബിന്ദുക്കളിലൂടെ കടന്നുപോകുന്നുണ്ടോ എന്ന് നോക്കിയാൽ മതി. അതായത് xy പ്രതലത്തിൽ കിടക്കുന്ന ഒരു വക്രരേഖയിൽകൂടി കടന്നുപോകുന്ന ലംബരേഖകളൊന്നും ആ വക്രത്തിന്റെ ഒന്നിലധികം ബിന്ദുവിലൂടെ കടന്നുപോകുന്നില്ലെങ്കിൽ ആ വക്രരേഖ ഒരു ഫലനത്തിന്റെ വക്രരേഖയാണ്.[1]

ഉദാഹരണങ്ങൾ

ഒരു ചരത്തിന്റെ ആരേഖം

 f(x, y) = sin(x^2) · cos(y^2) എന്ന ഫലനത്തിന്റെ ആരേഖം

${\displaystyle f(x)={\begin{cases}a,&{\text{if }}x=1,\\d,&{\text{if }}x=2,\\c,&{\text{if }}x=3,\end{cases}}}$

എന്ന ഫലനത്തിന്റെ ആരേഖം

${\displaystyle \{(1,a),(2,d),(3,c)\}.\,}$ആണ്

താഴെകൊടുത്തിരിയ്ക്കുന്ന ക്യൂബിക്കൽ ഫലനത്തിന്റെ ആരേഖം വലതുവശത്തു കൊടുത്തിരിയ്ക്കുന്നു.

രണ്ടു ചരങ്ങളുടെ ഫലനം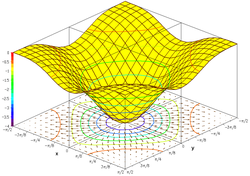

f(x, y) = −(cos(x^2) + cos(y^2))^2 എന്ന ഫലനത്തിന്റെ ആരേഖം.

${\displaystyle f(x,y)=\sin(x^{2})\cos(y^{2})\,}$

എന്ന ഫലനത്തിന്റെ ആരേഖം

${\displaystyle \{(x,y,\sin(x^{2})\cos(y^{2})):x{\text{ and }}y{\text{ are real numbers}}\}.}$

ഈ ഗണം മൂന്നു മാനങ്ങളുള്ള കോ ഓർഡിനേറ്റ് സിസ്റ്റത്തിൽ ചിത്രീകരിച്ചാൽ കിട്ടുന്നത് ഒരു ഉപരിതലമാണ്(surface) (ചിത്രം കാണുക). പലപ്പോഴും ഇത്തരം ഒരു ആരേഖം വരയ്ക്കുമ്പോൾ അതിന്റെ ഗ്രേഡിയന്റ് കൂടി വരയ്ക്കുന്നത് ഉപകാരപ്രദമായിരിയ്ക്കും. അതുപോലെ പല ലെവൽ കർവുകളും (ഒരേ ഔട്ട്പുട്ട് വില തരുന്ന ഇന്പുട് വിലകളുടെ ഗണമാണ് ലെവൽ സെറ്റ്. ഇതിനെ ഒരു ഉപരിതലത്തിൽ ചിത്രീകരിച്ചാൽ ലെവൽ കർവ് കിട്ടുന്നു.) ഇത്തരം ആരേഖത്തിൽ വരയ്ക്കാം. ഇത്തരം ലെവൽ കർവുകളെയും ഗ്രേഡിയന്റ്'കളെയും താഴെയുള്ള ഒരു പ്രതലത്തിലേക്ക് പ്രൊജക്റ്റ് ചെയ്തു വരയ്ക്കാവുന്നതാണ്.

അവലംബം

1. "Lecture 11: Graphs of Functions" (PDF). Department of Mathematics, University of Notre Dame. Retrieved 14 ഏപ്രിൽ 2018. If f is a function with domain A, then the graph of f is the set of all ordered pairs.
2. Charles C Pinter (2014) [1971]. A Book of Set Theory. Dover Publications. p. 49. ISBN 978-0-486-79549-2.

പുറംകണ്ണികൾ

• Weisstein, Eric W. "Function Graph." From MathWorld—A Wolfram Web Resource.