|
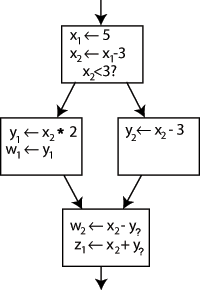
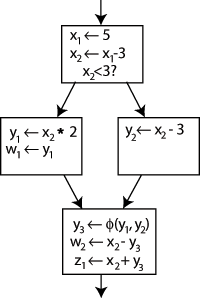
静的単一代入静的単一代入(せいてきたんいつだいにゅう、英: Static Single Assignment form, SSA)形式は、コンパイラ設計における 中間表現 (IR) のひとつで、各変数が一度のみ代入されるよう定義されたものである。もともとの中間表現における変数は「バージョン」に分割され、全ての変数の定義がバージョンを表現できるよう、通例新たな変数は元の名前に添え字を付けて表現される。SSA ではuse-def 連鎖が明示的であり、連鎖は要素を一つだけ持つ。 SSA はRon Cytron、Jeanne Ferrante、Barry Rosen、Mark Wegman、Ken Zadeck および IBM の研究者たちにより1980年代に開発された。 Scheme、ML、Haskell などの関数型言語のコンパイラでは、Fortran や C などのコンパイラで SSA の利用が期待される箇所で継続渡しスタイル (CPS) を用いるのが一般的である。SSA と CPS は形式的に等価であり、最適化やコードの変換などがいずれかに施された場合、もう片方にも同様に適用することができる。 SSA の利点変数の性質を簡単なものにすることにより様々なコンパイラ最適化を簡略化すると同時にその結果を改善することが SSA の第一の利点である。 例として、下記のようなコードを考える。 y := 1 y := 2 x := y 人間であれば、最初の代入が不要であり、3行目で使用されている y1 := 1 y2 := 2 x1 := y2 SSA を利用することにより、下記のコンパイラ最適化アルゴリズムを実現したり、あるいは改善することができる。 SSA への変換ツリー上のコードの SSA 形式への変換は、代入の対象を新たな変数に置き換え、変数の使用箇所をその定義箇所に到達する「バージョン付き」のものに置き換えるだけの基本的に簡潔な問題である。例として、下記のような制御フローグラフを考える。 "x x - 3" の左辺の名前を変え、それ以降 x を新たな名前に変えることができ、それでもプログラムは全く同じ動作をする。このことを利用して、SSA ではそれぞれに対して一度しか代入が行われない新たな二つの変数x1 と x2 を作成する。同様に、全ての変数に対してバージョンを区別するための添え字を与える。 ここで、各々の変数を使用している箇所がどの定義を参照しているかをただ一点を除いて把握している。最後のブロックの y は制御フローのどちらを通るかによって y1 と y2のどちらを参照するかが異なる。ではこれをどのようにして知るのか? その答えは、Φ (ファイ) 関数と呼ばれる特別な命令を最後のブロックの始めに追加することである。この命令は、どちらの制御フローから到達したのかによって y1 あるいは y2 を選択し y の新たな定義 y3 を生成する。 これにより、最後のブロックの y は y3 を用いることができ、いずれの場合でも正し値を得ることができる。 x についても Φ 関数を追加する必要があるか?という質問があるかもしれないが、答えは「不要」である。x のバージョンは x2 のみがこの箇所に到達しており、問題にはならない。 より一般的な質問として、任意の制御フローが与えられたとき、どこに、またどの変数に対して Φ 関数を挿入するべきか、という問題がある。これは難しい質問であるが、支配辺境(dominance frontier) と呼ばれる概念を用いて求める優れた方法がある。 ここで、Φ 関数は実際に実装されるものではなく、コンパイラに対して Φ 関数でグループとされる全ての変数の値をメモリやレジスタの同じ場所に配置するよう指示するマーカーである。 支配辺境を用いた最小 SSA の計算まず、dominator の概念が必要である。制御フローのノード A が別のノード B を 厳密に支配する とき、A に到達しなければ B に到達することがないことを意味する。これは、B に到達していれば A のコードが動作していることが分かるため有用である。また A が B を 支配するとき、A が B を厳密に支配するか、A = B であることを意味する。 ここで、支配辺境(dominance frontier)を次のように定義することができる。A は B を厳密に支配していないが、B の直前にあるノードのいくつかを支配しているとき( A が B の直前にあれば、A 自身)、ノード B は A の支配辺境内にあるものとする。A から見ると、これらは A を介さず、最初に登場する制御パス上のノードである。
for each node b
if the number of predecessors of b ? 2
for each p in predecessors of b
runner := p
while runner ≠ idom(b)
add b to runner’s dominance frontier set
runner := idom(runner)
注意:上記のコードでは、ノード n の前のノードは制御を n に渡す任意のノードであり、idom(n) がノードの n を直接支配する。 支配辺境を見つけるための効率的なアルゴリズムが存在し、論文 "Efficiently computing static single assignment form and the control dependence graph", by R. Cytron, J. Ferrante, B. Rosen, M. Wegman and F. Zadeck, ACM Trans. on Programming Languages and Systems 13(4) 1991 pp.451–490. において最初に示された。また "Modern compiler implementation in Java" by Andrew Appel (Cambridge University Press, 2002) も有用である。詳細は論文を参照のこと。 ライス大学の Keith D. Cooper, Timothy J. Harvey, Ken Kennedy は、論文 A Simple, Fast Dominance Algorithmにおいて、アルゴリズムを提唱した。このアルゴリズムはよく設計されたデータ構造を用いてパフォーマンスを改善させている。 Φ 関数の数を減らすための方法"最小の" SSA はそれぞれの名前に一度だけ変数が割り当てられることを保証し、もともとのプログラムでの名前の参照(変数の使用箇所)が 一意の名前を参照できることを保証する。(後者はコンパイラが各操作の対象となる変数の名前を特定できるようにするために必要である) しかし、Φ 関数の一部はデッドコードである可能性がある。このため、最小の SSA は必ずしも特定の手続きに必要な最小の Φ 関数を生成する必要はない。方法によっては、このような Φ 関数は無用であり、解析の効率を落としてしまう。 Pruned SSAPruned SSA 形式は非常に簡単な観察:すなわち「 Φ 関数は、それ以降に『生存している』変数にのみ必要であるに基づいており(ここでの「生存」とは変数の値が問題の Φ 関数から始まるパス上で使用されることを意味する)、変数が「生存」していなければ、Φ 関数の結果が使用されることはなく、Φ 関数による割り当ては無効である。 Pruned SSA を構築する場合には、Φ 関数を挿入する際に、生存変数情報(live variable information)を 用いて与えられた Φ 関数が必要なのかどうかを判断する。もともとの変数が Φ 関数を挿入する場所ですでに「生存」していなければ、Φ 関数は挿入されない。 刈り込み(pruning)を扱うもう一つの方法としてデッドコード削除の問題がある。Φ 関数は、入力プログラム内の変数の使用箇所のいずれかが Φ 関数に置き換えられる場合のみ SSA 形式に Φ 関数が各変数の参照箇所は、その変数を支配する最も近い定義に置き換えられる。 最低でも一箇所の参照箇所ないし生きた Φ 関数の引数を支配する最も近い定義であれば、生きているとみなすことができる。 Semi-pruned SSASemi-pruned SSA 形式 [1] は、生存変数の情報を求める比較的高い計算コストを要せず、Φ 関数の数を減らすための試みである。 Semi-pruned SSA は次の観察に基づいている:「変数が基本的なブロックに入る際に生存していなければ、 Φ 関数は必要ない」。 従って、SSA の構築の際、ブロックの局所変数に対する Φ 関数は省略可能である。 ブロックの局所変数のセットを求めるのは完全な生存変数解析を行うより簡単で高速に実行でき、pruned な SSA 形式を求めるより高速である。 一方、pruned な SSA 形式のほうが不要な Φ 関数は少ない。 SSA 形式からの変換SSA 形式は直接実行するために有用な形式ではないため、元のコードとの直接の対応関係を保持した中間コード上で用いられることが多い。これは、SSA を既存の中間コードの要素(基本ブロック、命令、オペランドなど)と SSA での対応する要素をマップした関数として構築することで実現できる。SSA が必要なくなればこれらのマップ関数は廃棄してよく、最適化された新しい IR が残る。 SSA 形式で最適化を行うと、非常に複雑な SSA の網目構造が作成される。すなわちオペランドが必ずしも同じ起点を持たない Φ 命令が存在することになる。このような場合色分け(color-out)アルゴリズムが用いられる。単純なアルゴリズムではそれぞれの以前のパスに従ってコピーを作成するが、 Φ 関数の出力ではなく入力となる起点のシンボルが多数できてしまう。SSA からコピーの回数を少なくするためのアルゴリズムが複数あり、大半のものは干渉グラフやコピーの融合を行うための近似を行う。 SSA の拡張SSA 形式の拡張は二種類に分類される。 改名戦略型の拡張は、異なった変数の改名基準を用いる。SSA 形式では値を代入する際に変数の名前を変えるが、これ以外の方法として各変数の参照時に名前を変える静的単一参照形式(static single use form)と、各変数の名前を代入されたときに変え、さらに変数が使用される条件節ごとに変える静的単一情報形式(static single information form)がある。 機能固有型拡張は、変数へ一度だけ代入を行うという性質を保ちつつ、新たな機能をモデル化できるよう新たな意味論を導入する。機能固有型の拡張は、配列、オブジェクトやポインタなどの高レベルプログラミング言語の機能をモデル化する。また投機実行や分岐予測などの低レベルのアーキテクチャ上の機能をモデル化する機能固有型の拡張も存在する。 配列配列の要素レベルに対する SSA としては、1998年に Kathleen Knobe と Vivek Sarkar による Array SSA[2]や2006年に Silvius Rus, Guobin He, Lawrence Rauchwerger による Region Array SSA[3] などが提案されている。 SSA形式を用いたコンパイラ前述のように理論的には1980年代にはその基本は確立されている。しかし、実際のコンパイラ(特に、プロプライエタリでないもの)への導入は比較的近年であり、従って、古いコンパイラは SSA 形式をコンパイルや最適化の一部でのみ使用し、ほとんどのものは全面的に SSA に依存することはない。SSA に大きく依存するコンパイラの例として、下記のものがある。
参考文献
関連項目外部リンク
|
Portal di Ensiklopedia Dunia