無限インパルス応答

無限インパルス応答（むげんインパルスおうとう、英: Infinite impulse response, IIR）はインパルス応答のうち無限長の時間においてゼロでない値を返すものである。有限インパルス応答 (FIR) と対比される。

この属性を持つシステムをIIRシステムと呼ぶ。最も単純なアナログIIRフィルタとしてRCフィルタがあり、1つの抵抗器 (R) と1つのコンデンサ (C) で形成される。このフィルタは、RC時定数で決定される指数関数的インパルス応答の特性を持つ。他にはチェビシェフフィルタ、バターワースフィルタ、ベッセルフィルタなどがある。

FIRフィルタとは異なり、IIRフィルタ設計では、フィルタの出力が明確に定義されない「時刻ゼロ」の場合を注意深く扱う必要がある。IIRフィルタは一般に、FIRフィルタに比較して高速で安価だが、バンドパスフィルタとしての性能や安定性が劣る。

IIRフィルタ

無限インパルス応答フィルタ（英: Infinite impulse response filter、IIRフィルタ）は無限インパルス応答で表現されるフィルタ/フィルタ回路である。巡回形フィルタとも呼ばれる[1]。

デジタルIIRフィルタ

デジタルIIRフィルタはIIRで表現されるデジタルフィルタである。

${\displaystyle \ b_{i}}$ を係数とする ${\displaystyle P}$ 次のフィードフォワードと${\displaystyle \ a_{i}}$ を係数とする ${\displaystyle Q}$ 次のフィードバックをもち、入出力を ${\displaystyle x[n]}$・${\displaystyle y[n]}$ とする離散時間システムを考える。システムは差分方程式を用いて次のように表現される。

${\displaystyle {\begin{aligned}a_{0}y[n]&=\sum _{i=0}^{P}b_{i}x[n-i]-\sum _{j=1}^{Q}a_{j}y[n-j]\\&=b_{0}x[n]+b_{1}x[n-1]+\cdots +b_{P}x[n-P]-a_{1}y[n-1]-a_{2}y[n-2]-\cdots -a_{Q}y[n-Q]\end{aligned}}}$

移項すると、

${\displaystyle \ \sum _{j=0}^{Q}a_{j}y[n-j]=\sum _{i=0}^{P}b_{i}x[n-i]}$

フィルタの伝達関数を見つけるため、上記方程式の両辺のZ変換を行う。このとき、Z変換のシフト性を利用する。

${\displaystyle \ \sum _{j=0}^{Q}a_{j}z^{-j}Y(z)=\sum _{i=0}^{P}b_{i}z^{-i}X(z)}$

ここで、伝達関数は次のように定義される。

${\displaystyle {\begin{aligned}H(z)&={\frac {Y(z)}{X(z)}}\\&={\frac {\displaystyle \sum _{i=0}^{P}b_{i}z^{-i}}{\displaystyle \sum _{j=0}^{Q}a_{j}z^{-j}}}\end{aligned}}}$

これらのデジタルIIRフィルタの設計は、アナログIIRフィルタに基づいてなされてきた。多くの場合、デジタルIIRフィルタを設計するにあたってまずアナログIIRフィルタ（例えば、チェビシェフフィルタ、バターワースフィルタ、楕円フィルタ）を設計し、インパルス不変法や双一次変換といった離散化技法を適用してデジタルに変換する。

ブロック図の説明

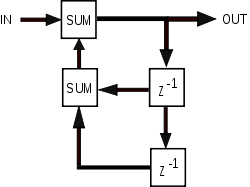単純なIIRフィルタのブロック図

右図は典型的なIIRフィルタのブロック図である。${\displaystyle z^{-1}}$ ブロックは単位遅延である。係数やフィードバック/フィードフォワード経路の数は実装依存である。

安定性

伝達関数により、そのシステムが有界入力-有界出力 (BIBO) 安定かどうかを判断できる。BIBO安定であるためには、伝達関数の全ての極の絶対値が1未満でなければならない。言い換えれば、全ての極は ${\displaystyle z}$-平面上の単位円の中に位置しなければならない。

極は、 ${\displaystyle H(z)}$ の分母が 0 となるような ${\displaystyle z}$ の値として定義される。

${\displaystyle \ 0=\sum _{j=0}^{Q}a_{j}z^{-j}}$

明らかに ${\displaystyle a_{j}\neq 0}$ ならば、極は z-平面の原点に位置しない。これは、FIRフィルタで常に極が原点に位置し、常に安定しているのと対照的である。

IIRフィルタは、FIRフィルタに比べて遷移域がシャープであることから、FIRフィルタよりも好まれることがある。

例

フィルタの伝達関数 H を次のように定義する。

${\displaystyle H(z)={\frac {B(z)}{A(z)}}={\frac {1}{1-az^{-1}}}}$ ここでROCは ${\displaystyle a<|z|}$ かつ ${\displaystyle 0<a<1}$

このときの極は a にあって、安定であり、因果性である。時間領域のインパルス応答は次のようになる。

${\displaystyle h(n)=a^{n}u(n)}$

これは ${\displaystyle n\geq 0}$ のとき、ゼロ以外の値をとる。

脚注

1. "フィードバックループが含まれており，このような構造のシステムを IIR ディジタルフィルタまたは巡回形ディジタルフィルタとよぶ" 雛元. (2008). 2-2 巡回形ディジタルフィルタ. 電子情報通信学会『知識の森』.

関連項目

• フィルタ回路
• 有限インパルス応答
• システム解析

外部リンク

• The fifth module of the BORES Signal Processing DSP course - Introduction to DSP