ja %E3%83%AA%E3%83%B3%E3%83%89%E3%83%A9%E3%83%BC%E5%BA%A7%E6%A8%99

相対論的物理において、リンドラー座標チャート (Rindler coordinate chart) は平坦な時空、すなわちミンコフスキー真空を表現するために重要かつ有用な座標チャート（英語版）である。リンドラー座標系は、ミンコフスキー空間内を一様加速度運動している基準系を記述する。特殊相対性理論によれば、一様な加速度を受ける粒子は双曲線運動（英語版）を行う。このような各粒子が静止して見えるのがリンドラー基準系である。

リンドラーチャートという名前は、この座標チャートの使用を普及させたウォルフガング・リンドラー（英語版）に由来する。ただし、アルバート・アインシュタインとネイサン・ローゼンの1935年の論文^[1]に既に使われていた概念である。

デカルトチャートとの関係

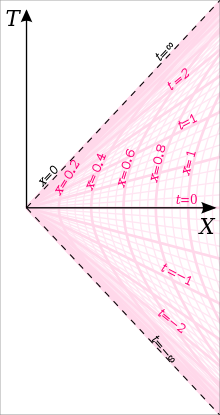
リンドラーチャートを得るには、まず下の計量を持つデカルトチャート（慣性系）から始める（ただし、 $c =1$ とする）。

\mathrm {d} s^{2}=-\mathrm {d} T^{2}+\mathrm {d} X^{2}+\mathrm {d} Y^{2}+\mathrm {d} Z^{2},\;^{\forall }T,X,Y,Z

$\scriptstyle 0\,<\,X\,<\,\infty ,\;-X\,<\,T\,<\,X$ の領域はよく「リンドラーのくさび」と呼ばれ、この領域では、固有時間がリンドラー座標時（後述）と同じに定義されたリンドラー観測者の（ $x =1$ の双曲線に沿った）固有加速度を $g$ とおくと、下の座標変換により新たなチャートが得られる。

t={\frac {1}{g}}\operatorname {arctanh} \left({\frac {T}{X}}\right),\;x={\sqrt {X^{2}-T^{2}}},\;y=Y,\;z=Z

逆変換は次のとおりになる。

T=x\,\sinh(gt),\;X=x\,\cosh(gt),\;Y=y,\;Z=z

リンドラーチャートでは、ミンコフスキー線素（英語版）は次のとおりに書ける。

\mathrm {d} s^{2}=-g^{2}x^{2}\mathrm {d} t^{2}+\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2},\;^{\forall }x>0,^{\forall }t,y,z

「リンドラー観測者」はリンドラー座標系において「静止」している、つまり $x, y, z$ を一定に保ち、時間とともに $t$ だけが変化する観測者として定義することができる。この世界線に留まるためには、観測者は一定の固有加速度（英語版）で加速する必要があり、 $x =0$ （リンドラー地平面）に近い観測者ほどより大きな固有加速度を持つ。すべてのリンドラー観測者は慣性系上において時刻 $T =0$ の瞬間には静止しており、この時刻には固有加速度 $g i$ の観測者は $X = 1/ g i$ （実際には $X = c 2 / g i$ だが、 $c =1$ の単位を使うものとする）の位置にあり、それぞれリンドラー座標系上ではリンドラー地平面から等距離を保つ。すべてのリンドラー観測者が各々の時計を $T =0$ でゼロにあわせたとすると、リンドラー座標系の定義時に、どのリンドラー観測者の固有時をリンドラー座標系の座標時 $t$ として採用するかを選ぶ余地がある。そして、選んだ観測者の固有加速度が前述の $g$ の値となる（リンドラー地平面からの距離が違う、その他のリンドラー観測者の固有時と、リンドラー座標時との関係は定数倍となる）^[2]。広く行われている慣習として、リンドラー座標系は固有加速度 $g =1$ のリンドラー観測者の固有時を座標時として採用する。その場合、上式の $g$ は消去される。

上式

t={\frac {1}{g}}\operatorname {arctanh} \left({\frac {T}{X}}\right),\;x={\sqrt {X^{2}-T^{2}}},\;y=Y,\;z=Z

は $c =1$ の単純化を行ってある。単純化を受けていない下式のほうが、加速度を $g$ としたときのリンドラー地平面までの距離を出すためには便利である。

{\begin{aligned}t&={\frac {c}{g}}\operatorname {arctanh} \left({\frac {cT}{X}}\right)\;{\overset {X\,\gg \,cT}{\approx }}\;{\frac {c^{2}T}{gX}}\\X&\approx {\frac {c^{2}T}{gt}}\;{\overset {T\,\approx \,t}{\approx }}\;{\frac {c^{2}}{g}}\end{aligned}}

この項のこれより下では、 $g =1$ および $c =1$ と置くこととし、 $X$ および $x$ の単位は $c^2/ g = 1$ となるように置くこととする。 $g = 1 光秒 /(秒 2)$ と置くのと $g = 1 光年 /(年 2)$ とするのとでは全く異ることに注意されたい。 $c =1$ とすることを決めても、固有加速度 $g$ の大きさを表わす単位には選択の余地がある。例えば、長さ ( $X$ および $x$ ) の単位として光年を使うものとすれば、時間 ( $T$ および $t$ ) の単位は年となり、 $g = 1 光年/(年 2)$ となり、これは約9.5 メートル/(秒²) に等しいが、長さ ( $X$ および $x$ ) の単位として光秒を使うものとすれば、時間 ( $T$ および $t$ ) の単位は秒となり $g = 1 光秒/(秒 2)$ 、すなわち 299792458 メートル/(秒²) に等しくなる。

リンドラー観測者

新しいチャートでは、次の余標構場^{[訳語疑問点]}をとるのが自然である。

\mathrm {d} \sigma ^{0}=-x\,\mathrm {d} t,\;\;d\sigma ^{1}=\mathrm {d} x,\;\;\mathrm {d} \sigma ^{2}=\mathrm {d} y,\;\;\mathrm {d} \sigma ^{3}=\mathrm {d} z

この双対標構場（英語版）^{[訳語疑問点]}は以下のようになる。

{\vec {e}}_{0}={\frac {1}{x}}\partial _{t},\;\;{\vec {e}}_{1}=\partial _{x},\;\;{\vec {e}}_{2}=\partial _{y},\;\;{\vec {e}}_{3}=\partial _{z}

これにより、（リンドラー座標系が覆う領域、つまりリンドラーのくさび上の）各世界点における接空間上に、「局所ローレンツ基準系」が定義される。時間的ベクトル場 $\scriptstyle {\vec {e}}_{0}$ の積分曲線は、リンドラー観測者と呼ばれる一連の観測者の世界線からなる時間的合同（英語版）^{[訳語疑問点]}を与える。リンドラーチャート上では、これらの世界線は $\scriptstyle x\;=\;x_{0},\;y\;=\;y_{0},\;z\;=\;z_{0}$ を表わす縦座標のようにみえる。上述の座標変換により、これらがもとのデカルトチャートでは双曲線に対応することがわかる。

いくつかのリンドラー観測者（紺の双曲線）をデカルトチャート上に描いたもの。45°の赤線はリンドラー地平面を表わす。リンドラー座標系は赤線よりも右にのみ定義される。

ローレンツ多様体上の一般の時間的合同と同様、この合同にも kinematic decomposition^{[訳語疑問点]} が存在する（レイチャウデューリ方程式を参照）。この場合、リンドラー観測者の合同の「膨張」と「渦度」は消える。膨張テンソルの消失は、「各観測者が隣の観測者と一定の距離を保つ」ということを意味する。渦度テンソルの消失は、各観測者の世界線が他の観測者の世界線に巻き付いたりしないということを意味する。これは局所的には「渦」が存在しないということである。

各観測者の加速ベクトル（英語版）は共変微分を用いて以下のように得られる。

\nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}={\frac {1}{x}}{\vec {e}}_{1}

つまり、各リンドラー観測者は $\scriptstyle \partial _{x}$ 方向に加速をしている。それぞれを見れば、各観測者は「一定の大きさの」加速度でこの方向に加速しており、その世界線は一定の曲率をもつため、ユークリッド幾何でいう円のローレンツ的な相似物になる。

リンドラー観測者は「渦無し」であるため、「超曲面直交」^{[訳語疑問点]} となる。直交超曲面断片は $\scriptstyle t\;=\;t_{0}$ である。これらはリンドラーチャート上には水平な半平面として現われ、デカルトチャート上には $\scriptstyle T\;=\;X\;=\;0$ を通る半平面として現われる（上図参照）。 $d t = 0$ の線素については、通常のユークリッド幾何 $d σ 2 = d x 2 + d y 2 + d z 2; \forall x > 0, \forall y, z$ が満たされることがわかる。したがって、リンドラーチャートの空間座標はリンドラー観測者が相互に静止しているということをとても単純に反映していると言える。この、リンドラー観測者の剛体性については後述する。

「パラドックス的」性質

$x$ 座標がより小さな定数であるリンドラー観測者は、より大きな加速度で加速して追随していることに注意されたい。ニュートン力学的では、同じ距離を保つ観測者は同一の加速度をもっていなければならないので、この事実には驚くかもしれない。しかし、相対論的物理学では、外力により棒を（長軸に並行に）加速するとき、後端点は先端点よりも強く加速しなければ最終的には破壊されてしまう。これはローレンツ収縮（英語版）から言えることである。棒が加速するにつれ、速度は増加し長さは減少していく。棒は短くなっていくので、後端は先端よりも強く加速する必要がある。別の言い方をすると、後端は同じだけの速度変化をより短い時間で行わなければならないということである。この事を微分方程式にすると、ある距離で後端の加速度は発散し、リンドラー地平面が生じることがわかる。

この現象は、よく知られた「パラドックス」、ベルの宇宙船パラドックス（英語版）の基礎となっている。しかし、これは相対論的力学の単純な帰結である。このことを示す一つの方法は、加速度ベクトルとは対応する世界線の曲率（英語版）であると考えることである。ここで、「リンドラー観測者の世界線はユークリッド空間でいう同心円の相似物」であるから、「内側のレーンのスピードスケーターほど外側のレーンよりも（単位弧長あたり）速く曲がる」というよく知られた事実のローレンツ幾何版だと喩えることができる。

ミンコフスキー観測者

別の基準系を導入してみよう。ミンコフスキーチャートにおける自然な選択は、以下のようなものである。

{\vec {f}}_{0}=\partial _{T},\;{\vec {f}}_{1}=\partial _{X},\;{\vec {f}}_{2}=\partial _{Y},\;{\vec {f}}_{3}=\partial _{Z}

これらのベクトル場を上述の変換で変換すると、（リンドラーのくさびの範囲内で）リンドラーチャート上ではこの基準系は以下のようになることがわかる。

{\begin{aligned}{\vec {f}}_{0}&={\frac {1}{x}}\cosh(t)\,\partial _{t}-\sinh(t)\,\partial _{x}\\{\vec {f}}_{1}&=-{\frac {1}{x}}\sinh(t)\,\partial _{t}+\cosh(t)\,\partial _{x}\\{\vec {f}}_{2}&=\partial _{y},\;{\vec {f}}_{3}=\partial _{z}\end{aligned}}

時間的単位ベクトル場 $\scriptstyle {\vec {f}}_{0}$ により定義される時間的合同の力学的分解を計算すると、ここでも膨張と渦度は消失し、加えて加速度ベクトルも消失して $\scriptstyle \nabla _{{\vec {f}}_{0}}{\vec {f}}_{0}\;=\;0$ となることがわかる。換言すれば、これは「測地合同」である。すなわち、観測者は「慣性運動」状態にある。元のデカルトチャートでは、これらミンコフスキー観測者は静止状態にある。

リンドラーチャートでは、ミンコフスキー観測者の世界線は座標面 $\scriptstyle x\;=\;0$ に漸近する双曲正割曲線として現われる。具体的には、リンドラー座標系では、世界点 $\scriptstyle t\;=\;t_{0},\;x\;=\;x_{0},\;y\;=\;y_{0},\;z\;=\;z_{0}$ を通過するミンコフスキー観測者の世界線は以下の曲線となる。

{\begin{aligned}t&=\operatorname {arctanh} \left({\frac {s}{x_{0}}}\right),\;-x_{0}<s<x_{0}\\x&={\sqrt {x_{0}^{2}-s^{2}}},\;-x_{0}<s<x_{0}\\y&=y_{0}\\z&=z_{0}\end{aligned}}

ここで、 $\scriptstyle s$ はこのミンコフスキー観測者の固有時間である。この観測者の履歴の一部しかリンドラーチャートには描かれないことに注意されたい。このことはリンドラーチャートが測地完全（英語版）ではないことを明示している。時間的測地線は有限の固有時間のうちにリンドラーチャートの範囲外に出てしまえるのである。もちろん、我々はリンドラーチャートは測地完全である元のデカルトチャートの一部分しか覆わないので、リンドラーチャートが測地完全ではありえないことは当然のことである。

上図には、 $\scriptstyle x_{0}\;=\;1$ の場合を、 $\scriptstyle s\,\in \,\left\{-{\frac {1}{2}},\;0,\;{\frac {1}{2}}\right\}$ における（縮尺を併せかつ適切にブーストされた）光円錐と共に描いてある。

リンドラー地平面

リンドラー座標系チャートは $x = 0$ に計量の行列式が 0 になってしまう「座標特異点」を持つ。これは $x \to 0$ の極限においてリンドラー観測者の加速度が発散してしまうために生じるものである。リンドラーのくさびを描いた図から読み取れる通り、リンドラーチャート上の位置 $x = 0$ はデカルトチャート上の位置 $T 2 = X 2, X > 0$ に対応し、これは二つのヌル測地合同下の半平面から成る。

測地線

リンドラーチャート上における測地方程式は測地ラグランジアンからすぐに得ることができ、以下のようになる。

{\ddot {t}}+{\frac {2}{x}}\,{\dot {x}}\,{\dot {t}}=0,\;{\ddot {x}}+x\,{\dot {t}}^{2}=0,\;{\ddot {y}}=0,\;{\ddot {z}}=0

もちろん、元のデカルトチャート上では測地線は直線として現われるから、これを座標変換してやることによってリンドラーチャート上での測地線を得ることはできる。しかし、元のチャートとは独立に測地線を得ることは有意義なので、この節ではそれを行う。

$t =0$ の空間的超断面に投影した、いくつか選んだリンドラー観測者のヌル測地線（黒の半円状弧）。リンドラー地平面は紫の平面として描かれている。

第一、第三、第四の式から、直ちに「一次積分」を得ることができる。

{\dot {t}}={\frac {E}{x^{2}}},\;\;{\dot {y}}=P,\;\;{\dot {z}}=Q

しかし、線素からは $\scriptstyle \epsilon \;=\;-x^{2}\,{\dot {t}}^{2}\,+\,{\dot {x}}^{2}\,+\,{\dot {y}}^{2}\,+\,{\dot {z}}^{2}$ が得られる。ここで、 $\scriptstyle \epsilon \;\in \;\left\{-1,\,0,\,1\right\}$ はそれぞれ時間的、光的、空間的測地線に対応する。これにより四つめの一次積分が以下のように得られる。

{\dot {x}}^{2}=\left(\epsilon +{\frac {E^{2}}{x^{2}}}\right)-P^{2}-Q^{2}

.

これで測地方程式の完全な解が得られた。

ヌル測地線（英語版）の場合、 $\scriptstyle {\frac {E^{2}}{x^{2}}}\,-\,P^{2}\,-\,Q^{2}$ から $E$ が非零のとき、 $x$ 座標は区間 $\scriptstyle 0\,<\,x\,<\,{\frac {E}{\sqrt {P^{2}\,+\,Q^{2}}}}$ を覆うことがわかる。

リンドラーのくさび上の任意の世界点を通るヌル測地線を得るのに完全な七つのパラメータは以下のようになる。

{\begin{aligned}t-t_{0}&=\operatorname {arctanh} \left({\frac {1}{E}}\left[s\left(P^{2}+Q^{2}\right)-{\sqrt {E^{2}-\left(P^{2}+Q^{2}\right)x_{0}^{2}}}\right]\right)+\\&\quad \quad \operatorname {arctanh} \left({\frac {1}{E}}{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}\right)\\x&={\sqrt {x_{0}^{2}+2s{\sqrt {E^{2}-(P^{2}+Q^{2})x_{0}^{2}}}-s^{2}(P^{2}+Q^{2})}}\\y-y_{0}&=Ps;\;\;z-z_{0}=Qs\end{aligned}}

いくつか選んだある世界点を通るヌル測地線の「軌跡」をプロットすると（つまり、 $t = 0$ の超断面に投影すると）、リンドラー地平面に直交する半円と見紛うような曲線群が得られる（図を参照）。

フェルマー計量

リンドラーチャート上では、任意の空間的超断面上に投影したヌル測地線が単純に半円状の弧になることは、上に示した一般解から直接確かめることができるが、これを示す非常に単純な方法がある。静的時空（英語版）とは、渦なしの時間的キリングベクトル場が存在する時空である。このとき、（慣性運動しているとは限らない）対応する定常観測者に直交する一連の（同一）空間的超断面を一意に定義することができる。このことから、これら任意の超断面上に、時空から受け継いだ元の計量に共形に関連付けられる新しい計量を、その計量（これは三次元リーマン多様体上のリーマン計量であることに注意）の測地線が時空のヌル測地線の投影と正に一致するような性質を持つように定義することができる。この新しい計量は「フェルマー計量」と呼ばれ、線素が

\mathrm {d} s^{2}=g_{00}\,\mathrm {d} t^{2}+g_{jk}\,\mathrm {d} x^{j}\,\mathrm {d} x^{k},\;\;j,\;k\in \{1,2,3\}

で与えられるような座標系が付与されている定常時空では、 $t = 0$ におけるフェルマー計量は単純に

\mathrm {d} \rho ^{2}={\frac {1}{-g_{00}}}\left(g_{jk}\,\mathrm {d} x^{j}\,\mathrm {d} x^{k}\right)

となる（ここで、計量の係数は $t = 0$ で評価されたものとする）。

リンドラーチャートでは、時間的並進 $\partial t$ が上述の時間的キリングベクトルであるから、これは定常時空である（これはミンコフスキー時空がアインシュタイン方程式の自明な静的真空解であることからも驚くべきことではない）。したがって、リンドラー観測者のフェルマー計量は直ちに以下のように書ける。

\mathrm {d} \rho ^{2}={\frac {1}{x^{2}}}\left(\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}\right),\;\;^{\forall }x>0,\;\;^{\forall }y,z

しかし、これはよく知られた「三次元双曲空間」 $H 3$ の上半空間チャートにおける線素である。これは、複素解析の学生が代々「共形写像問題」（とその他多くの問題）に関連して習わされる、よく知られた双曲平面 $H 2$ の上半平面チャートにごく似ており、多くの数学に関心のある読者にとっては $H 2$ の測地線が単に（実軸で表わされる無限大を中心とする円に直交する）半円になることは既知であろう。

対称性

リンドラーチャートはミンコフスキー時空の座標チャートであるから、十個の互いに線形独立なキリングベクトル場があることが予期される。実際に、デカルトチャートでは一つの時間並進、三つの空間並進、三つの空間回転、三つのローレンツブーストに対応する部分群をもつ、十個の互いに線形独立なキリングベクトル場を容易に見付けることができる。付随して、これらはミンコフスキー時空の対称性群たる（固有等時）ポアンカレ群を生成する。

しかし、キリングベクトル方程式を直接書き下して解くのが教育的によい。四つの見慣れたキリングベクトル場

\partial _{t},\;\;\partial _{y},\;\;\partial _{z},\;\;-z\,\partial _{y}+y\,\partial _{z}

（時間並進、加速方向と直交する空間並進、および加速方向と直交する空間回転）に加えて六つ、

{\begin{aligned}&\exp(\pm t)\,\left({\frac {y}{x}}\,\partial _{t}\pm \left[y\,\partial _{x}-x\,\partial _{y}\right]\right)\\&\exp(\pm t)\,\left({\frac {z}{x}}\,\partial _{t}\pm \left[z\,\partial _{x}-x\,\partial _{z}\right]\right)\\&\exp(\pm t)\,\left({\frac {1}{x}}\,\partial _{t}\pm \partial _{x}\right)\end{aligned}}

（複号同順）が得られる。標準的生成子との関係は練習問題に残しておく。ここで、デカルトチャートにおける $\partial T$ に相当する生成子を得ることはできるが、リンドラーのくさびはこの並進に対して明らかに不変ではない。なぜこうなるのだろうか？答えは、滑らかな多様体上の偏微分方程式系により定義されるどんなものとも同じで、キリング方程式は一般に局所解は持つが大域解があるとはかぎらないということである。つまり、パラメータが適切ならばキリングフローを局所近傍に定義することはできるが、大域的（英語版）に well-defined^{[訳語疑問点]} なフローが得られるとは限らない。これはローレンツ多様体そのものの問題ではなく、一般の滑らかな多様体の研究において同様な問題は発生する。

距離の定義

リンドラーチャートの研究から得られる多くの教訓の一つに、いくつかの異なる（しかし筋の通った）リンドラー観測者にとっての距離概念がありうるという事実が挙げられる。

二人のリンドラー観測者（紺の縦線）の間の「レーダー距離」の作業的意味。リンドラー地平面は左端の赤い縦線で示されている。レーダーパルスの世界線と共に、世界点 A（中央下）, B（右中央）, C（中央上）における（適切にスケールした）光円錐も示す。

最初の一つは、ここまでに暗黙に採用されていたもので、空間的超断面 $t = t 0$ 上における誘導リーマン計量である。これを、この誘導リーマン計量に対応するという意味で「定規距離」と呼ぼう。しかし、この距離の作業的な意味は直ちに明らかなわけではない。

物理測定の立場からいってより自然な二つの世界線の間の距離概念は、「レーダー距離」である。これはある観測者の世界線上の世界点 A からヌル測地線を小物体に向けて飛ばし、世界点 B で反射して観測者に返し、世界点 C で受けとるのにかかった往復時間を観測者の持つ理想時計で測り、割ることで計算できる。

（ミンコフスキー時空では、幸いにも二つの世界線の間に複数のヌル測地線が存在するという可能性については考えなくてもよい。しかし、これを宇宙論的モデルに適用するのはそう単純にはいかない。この二人の観測者間の距離概念は、観測者の入れ替えに対して対称な概念であることに注意が必要である。）

具体的には、座標 $x = x 0, y = 0, z = 0$ のリンドラー観測者と座標 $x = x 0 + h, y = 0, z = 0$ （前者は後続であるから、追随するためにより強い加速度をうけていることに注意。）リンドラー線素において $d y = 0, d z = 0$ と置くことにより、すぐに加速度方向のヌル測地線の満す方程式を得ることができる。

t-t_{0}=\log(x/x_{0})

したがって、これら二人の観測者の間のレーダー距離は以下で与えられる。

x_{0}\,\log \left(1+{\frac {h}{x_{0}}}\right)=h-{\frac {h^{2}}{2\,x_{0}}}+O\left(h^{3}\right)

これは定規距離より若干小さいが、近傍の観測者間では違いは無視できる。

三つめの距離概念は次のように説明される。（点ではなく）なんらかの物体の上に置かれた単位円を観測者の場所から見たときの見込み角を計測する。これを「光学直径距離」と呼ぶ。ミンコフスキー時空上におけるヌル測地線の単純な性質から、（加速方向に沿って並んだ）リンドラー観測者間の光学的距離は容易に決定できる。スケッチを書けば、光学直径距離が $\scriptstyle h\,+\,{\frac {1}{x_{0}}}\,+\,O\left(h^{3}\right)$ のようにスケールすることは納得できるだろう。したがって、後続の観測者が先行する観測者までの距離を推定する（ $h > 0$ の）場合、レーダー距離よりも若干長い定規距離よりも光学距離が若干長いことになる。先行する観測者から後続の観測者までの距離は読者に考えて欲しい。

ほかにも距離概念はあるが、要点は明確である。これらの様々な概念による、あるリンドラー観測者間の距離の値は一般的に一致しないが、全ての概念で「リンドラー観測者は一定の距離を保つ」ということは一致するのである。近傍のリンドラー観測者の間が相互に定常であることは、リンドラー合同の膨張テンソルが恒等的にゼロであることの帰結である。しかし、この剛体性はより大きなスケールでも保たれることはここまで見てきた通りである。この剛体性は、相対論的物理学においては（少くとも不均一な応力をかけることなしに）棒を剛体的に加速することはできない（および円板を剛体的に回転させることはできない）というよく知られた事実に対するに、真に特筆すべき性質である。この事実を明らかにする最も簡単な方法は、ニュートン力学では剛体を「蹴った」場合、その全ての物質要素は瞬時に運動状態を変える。これは当然のごとく、光速よりも速く物理的効果のある情報を伝えることはできないとする相対性原理に反している。

この帰結として、棒の長さに沿って各所に外力を加えるときは、棒の異る箇所には異なる大きさの加速度を与えなければ、いつか棒は限界を越えて膨張し最終的には破壊されるということを示すことができる。換言すれば、破壊されずに加速され続ける棒はその長さに沿って変化する応力を感じなければならないということである。さらには、力を時間的に変化させるどんな試行実験でも、「蹴る」にしろ徐々に加速するにしろ、物体の違う部分が外力に対して光速を超えて反応を示すような、相対論とは相容れないモデルを避けなければならないという問題からは避けて通れないということが言える。

定規距離の作業的意味の問題に戻ると、観測者間で非常にゆっくりと小さな定規を片方の端からもう片方の端まで繰り返し手渡していった場合に得られる距離に他ならないことがわかる。しかし、この理解を詳細にわたって正当化するためには、なんらかの物性モデルについての考察が必要となる。

曲がった時空への一般化

ここまで説明してきたリンドラー座標は、フェルミ正規座標（英語版）という形で曲がった時空へと一般化できる。この一般化は根本的には適切な正規直交四つ組の構築と、それらのフェルミ・ウォーカー移動による適当なトラジェクトリ上の移動に関わっている。詳しくは、Ni & Zimmerman (1978)を参照されたい。この一般化により、実際に地球上の研究室から慣性および重力の効果を研究したり、さらにはより興味深い慣性・重力カップリング効果を研究したりすることができる。

脚注

^ Einstein, Albert; Rosen, Nathan (1935). “A Particle Problem in the General Theory of Relativity”. Physical Review 48: 73. Bibcode: 1935PhRv...48...73E. doi:10.1103/PhysRev.48.73.
^ Koks, Don: Explorations in Mathematical Physics (2006), pp. 240-252

参照文献

背景知識として有用:

Boothby, William M. (1986). An Introduction to Differentiable Manifolds and Riemannian Geometry. New York: Academic Press. ISBN 0-12-116052-1 See Chapter 4 for background concerning vector fields on smooth manifolds.
Frankel, Theodore (1979). Gravitational Curvature: an Introduction to Einstein's Theory. San Francisco : W. H. Freeman. ISBN 0-7167-1062-5 See Chapter 8 for a derivation of the Fermat metric.

リンドラー座標系:

Rindler, Wolfgang (1969). Essential Relativity. New York, Van Nostrand Reinhold Co. doi:10.1007/978-1-4757-1135-6. ISBN 978-0-387-90201-2

Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0 See Section 6.6.
Rindler, Wolfgang (2001). Relativity: Special, General and Cosmological. Oxford: Oxford University Press. ISBN 0-19-850836-0
Ni, Wei-Tou; Zimmermann, Mark (1978). “Inertial and gravitational effects in the proper reference frame of an accelerated, rotating observer”. Physical Review D 17 (6): 1473–1476. Bibcode: 1978PhRvD..17.1473N. doi:10.1103/PhysRevD.17.1473.

リンドラー地平面:

Jacobson, Ted; Parenti, Renaud (2003). “Horizon Entropy”. Found. Phys. 33 (2): 323–348. doi:10.1023/A:1023785123428. eprint version
“Analogue Gravity”. Living Reviews in Relativity. 2006年5月6日閲覧。

[1] Einstein, Albert; Rosen, Nathan (1935). “A Particle Problem in the General Theory of Relativity”. Physical Review 48: 73. Bibcode: 1935PhRv...48...73E. doi:10.1103/PhysRev.48.73.

[2] Koks, Don: Explorations in Mathematical Physics (2006), pp. 240-252

[1]

[2]

リンドラー座標