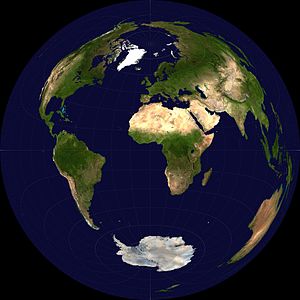
ランベルト正積方位図法

ランベルト正積方位図法（北極を中心とした地図、北半球のみ）。極点を中心とした投影は、投影される扇形の中心角を360°（すなわち円板）に設定した場合のランベルト正積円錐図法に相当する。

ランベルト正積方位図法（経緯度ともに0度を中心とした衛星写真）

ランベルト正積方位図法（ランベルトせいせきほういずほう）とは、地図投影法の一種であり、方位図法（地図の中心からの方位が正しく示される）および正積図法（英語版）（面積が正しく示される）の両方の性質を持つ。

北極点もしくは南極点を基準点（中心）とした場合、経線は中心から放射状に、緯線は基準点を中心とする同心円に描かれる。面積が正しく表されるよう、緯線の間隔は特に図の外側（基準点に対して赤道より遠い側の半球）で狭くなっている。中心付近の歪みは比較的小さいので、大陸図や分布図に用いられる。

緯度が l° である緯圏を投射図上に描くための半径 r は、r = 2 R sin((90－l)/2) （Rは地球の半径）で与えられる。

同様に世界全体が円形に描かれる図法には、正距方位図法などがある。

定義

球とそれに S で接する平面の断面図。対蹠点を除く球面上の全ての点は、S を中心とする円弧に沿って平面に投影される。

ランベルト正積方位図法を定めるには、球と、その球にある点 S で接する平面を考える。P を S の対蹠点でない球上の任意の点とする。d を S と P の三次元空間での距離とすれば（球面に沿っての距離ではない）、この投影によって P は平面上で S から d の距離にある点 P′ に移される。

より厳密にいえば以下のようになる。S を中心とし、P を通り、今考えている平面と直交するような円がただひとつ存在する。この円は平面と2点で交わるので、P′ を P に近い方として定める。これが投影後の点である（図を参照）。S の対蹠点はこの円がただひとつに定まらないため投影から省かれる。S は半径 0 の円弧に沿って自身に投影される[1]。

コンピュータ上で投影を行うためには明示的な式を与える必要がある。単位球面（すなわち x^2 + y^2 + z^2 = 1 を満たす三次元空間 ${\displaystyle \mathbb {R} ^{3}}$ 上の点 (x, y, z) の集合）上の S = (0, 0, -1) を図の中心とする投影を考えてみよう。デカルト座標で球面上の点 ${\displaystyle (x,y,z)}$ と平面上の点 ${\displaystyle (X,Y)}$ を表すこととすると、この投影とその逆写像は次で表される。

${\displaystyle (X,Y)=\left({\sqrt {\frac {2}{1-z}}}x,{\sqrt {\frac {2}{1-z}}}y\right),}$

${\displaystyle (x,y,z)=\left({\sqrt {1-{\frac {X^{2}+Y^{2}}{4}}}}X,{\sqrt {1-{\frac {X^{2}+Y^{2}}{4}}}}Y,-1+{\frac {X^{2}+Y^{2}}{2}}\right).}$

球面座標 (φ, θ) （φ が天頂からの角度、θ が方位角）と極座標 (R, Θ) を用いると次のように表される[1]。

${\displaystyle (R,\Theta )=\left(2\cos(\phi /2),\theta \right),}$

${\displaystyle (\phi ,\theta )=\left(2\arccos(R/2),\Theta \right).}$

円柱座標系 (r, θ, z) と極座標 (R, Θ) では

${\displaystyle (R,\Theta )=\left({\sqrt {2(1+z)}},\theta \right),}$

${\displaystyle (r,\theta ,z)=\left(R{\sqrt {1-{\frac {R^{2}}{4}}}},\Theta ,-1+{\frac {R^{2}}{2}}\right).}$

となる。

他の点を中心とする場合や半径が 1 以外の球面に対して定義される射影も同様の式で表現される[2]。

性質

前節で述べたとおり、単位球面に対するランベルト正積方位図法による投射は (0, 0, 1) では定義されない。それ以外の点は、平面上で中心が原点 (0, 0), 半径 2 の開円板に移される。球面上の点 (0, 0, -1) は (0, 0) へ、赤道 z = 0 は半径 ${\displaystyle {\sqrt {2}}}$, 中心 (0, 0) の円に、南半球 z < 0 はその円に含まれる開円板に移ることになる。

この射影は球面（から点 (0, 0, 1) を除いたもの）と半径 2 の開円板との微分同相写像 （両方向について無限回微分可能な全単射）である。正積図法であることは球面上の面素の面積を、逆写像を用いて変数変換して計算することで示すことができる。デカルト座標では

${\displaystyle dA=dX\;dY.}$

したがって球上で面積を測ることは円板上（地図上）で対応する部分の面積を測ることと同等であることが分かる。

一方、この図法では球面上の曲線間の角度の関係は保存されない。一般に、球面の一部と平面間の写像では角度と面積を両方保存することはできない（もしそれが可能なら、それは局所的等長写像となり、ガウス曲率が保存されるはずであるが、球面と円板はこれが異なるので、これは不可能である）。この、平らな図では球面の一部分を完全に表すことはできないということは、地図学における基本的な問題である。

結果として、球面上の区域は地図上ではかなり形が歪むことがある。この歪みはとくに図法の中心 (0, 0, -1) から離れたところで顕著である。このため、実用上はこの図法で描く地図は半球までに制限するということがよく行われる。もう半球は必要なら別の図で描けばよい。

脚注

1. ^ Borradaile (2003).
2. “Coordinate Conversions and Transformations including Formulas”. International Association of Oil & Gas Producers (2009年11月). 2010年10月6日閲覧。

参考文献

• Borradaile, Graham J. (2003). Statistics of Earth science data. Berlin: Springer-Verlag. ISBN 3-540-43603-0 
• Do Carmo, Manfredo P. (1976). Differential geometry of curves and surfaces. Englewood Cliffs, New Jersey: Prentice Hall. ISBN 0-13-212589-7 
• Hobbs, Bruce E., Means, Winthrop D., and Williams, Paul F. (1976). An outline of structural geology. New York: John Wiley & Sons, Inc. ISBN 0-471-40156-0 
• Ramsay, John G. (1967). Folding and fracturing of rocks. New York: McGraw-Hill 
• Spivak, Michael (1999). A comprehensive introduction to differential geometry. Houston, Texas: Publish or Perish. ISBN 0-914098-70-5 

関連項目

• ランベルト正積円錐図法
• ランベルト正積円筒図法
• ランベルト正角円錐図法
• ヨハン・ハインリヒ・ランベルト