„ā≥„ÉÉ„ÉČ„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥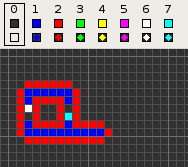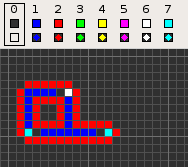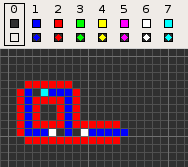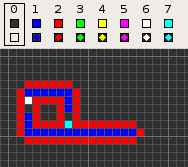 „ā≥„ÉÉ„ÉČ„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥ÔľąCodd's cellular automatonԾȄĀĮ„ÄĀ1968ŚĻī„ÄĀ„ā§„āģ„É™„āĻšļļŤ®ąÁģóś©üÁßĎŚ≠¶ŤÄÖ„ā®„ÉČ„ā¨„Éľ„ÉĽF„ÉĽ„ā≥„ÉÉ„ÉČ„ĀĆŤÄÉś°ą„Āó„Āü„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥ (CA)„Äā„Éē„ā©„É≥„ÉĽ„Éé„ā§„Éě„É≥„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„Ā®ŚźĆśßė„ĀģŤ®ąÁģó„ÉĽśßčÁĮČšłáŤÉĹśÄß„āíśúČ„Āó„Ā¶„ĀĄ„āč„ĀĆ„ÄĀ„Éē„ā©„É≥„ÉĽ„Éé„ā§„Éě„É≥„ĀģCA„ĀĆ29Áä∂śÖč„Ā†„Ā£„Āü„Āģ„ĀęŚĮĺ„Āó„Ā¶8Áä∂śÖč„Āßśßčśąź„Āē„āĆ„Ā¶„ĀĄ„āč„Äā„ā≥„ÉÉ„ÉČ„ĀĮ„ĀĚ„ĀģCA„Āß universal constructor „Āģ„āą„ĀÜ„ĀęŤá™Ś∑ĪŤ§áŤ£Ĺś©üśĘį„āíśßčśąźŚŹĮŤÉĹ„Āß„Āā„āč„Āď„Ā®„āíÁ§ļ„Āó„Āü„ĀĆ„ÄĀ2009ŚĻī„Āĺ„Āß„ĀĚ„āĆ„ĀĆŚģĆŚÖ®„ĀęŚģüŤ£Ö„Āē„āĆ„āč„Āď„Ā®„ĀĮ„Ā™„Āč„Ā£„Āü„Äā ś≠īŚŹ≤1940ŚĻīšĽ£„Āč„āČ50ŚĻīšĽ£„Āę„Āč„ĀĎ„Ā¶„ÄĀ„āł„Éß„É≥„ÉĽ„Éē„ā©„É≥„ÉĽ„Éé„ā§„Éě„É≥„ĀĮšĽ•šłč„Āģ„āą„ĀÜ„Ā™ŚēŹť°Ć„ā휏źÁ§ļ„Āó„Āü[1]:
ŚĹľ„ĀĮ29„ĀģÁä∂śÖč„āíśĆĀ„Ā§„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„āíśßčÁĮČ„Āó„ÄĀ„ĀĚ„āĆ„āíšĹŅ„Ā£„Ā¶ universal constructor „āíÁĒü„ĀŅŚáļ„Āó„Āü„Äā1968ŚĻī„ÄĀ„ā≥„ÉÉ„ÉČ„ĀĮ„āā„Ā£„Ā®ŚćėÁīĒ„Ā™ 8 Áä∂śÖč„Ā†„ĀĎ„Āč„āČ„Ā™„āč„Éě„ā∑„É≥„āíÁôļŤ¶č„Āó„Āü[2]„Äā„Āó„Āü„ĀĆ„Ā£„Ā¶„Éē„ā©„É≥„ÉĽ„Éé„ā§„Éě„É≥„ĀģŚēŹť°Ć„ĀĮś¨°„Āģ„āą„ĀÜ„ĀęšŅģś≠£„Āē„āĆ„Ā™„ĀĎ„āĆ„Āį„Ā™„āČ„Ā™„ĀŹ„Ā™„Ā£„Āü:
„ā≥„ÉÉ„ÉČ„ĀģCA„ĀģÁôļŤ°®„Āč„āČ3ŚĻīŚĺĆ„ÄĀEdwin Roger Banks „ĀĆŚćöŚ£ęŤęĖśĖá„Āߍ®ąÁģó„Āä„āą„Ā≥śßčÁĮČ„ĀģšłáŤÉĹśÄß„āíÁ§ļ„Āô4Áä∂śÖč„ĀģCA„ā휏źÁ§ļ„Āó„Āü„Äā„Āü„Ā†„Āó„ÄĀ„ā≥„ÉÉ„ÉČ„āāBanks„āā„ĀĚ„ĀģCAšłä„ĀģŤá™Ś∑ĪŤ§áŤ£Ĺś©üśĘį„Āģśßčśąź„āíÁ§ļ„Āó„Ā¶„ĀĄ„Ā™„ĀĄ[3]„Äā1973ŚĻī„ÄĀJohn Devore „ĀĆšŅģŚ£ęŤęĖśĖá„Āß„ā≥„ÉÉ„ÉČ„ĀģCA„āíśĒĻŤČĮ„Āó„Ā¶Ś§ßŚĻÖ„ĀęŚćėÁīĒŚĆĖ„Āó„ÄĀŚĹďśôā„Āģ„ā≥„É≥„ÉĒ„É•„Éľ„āŅšłä„ĀߌģüŤ£ÖŚŹĮŤÉĹ„Ā™Ť¶Źś®°„Āę„Āó„Āü„Äā„Āó„Āč„Āó„ÄĀŤá™Ś∑ĪŤ§áŤ£Ĺ„Āģ„Āü„āĀ„Āģ„Éá„Éľ„āŅ„ÉÜ„Éľ„Éó„ĀĮťĚ쌳ł„Āęťē∑„ĀŹ„ÄĀŚģüťöõ„ĀęŤá™Ś∑ĪŤ§áŤ£Ĺ„ĀĆÁĘļŤ™ć„Āß„Āć„Āü„Āģ„ĀĮ Golly „Ā®„ĀĄ„ĀÜ„Éó„É≠„āį„É©„Ɇ„ĀĆťĖčÁôļ„Āē„āĆ„Ā¶„Āč„āČ„Āģ„Āď„Ā®„Āß„Āā„āč„Äā„āĮ„É™„āĻ„Éą„Éē„ā°„Éľ„ÉĽ„É©„É≥„āį„Éą„É≥„ĀĮ1984ŚĻī„ÄĀ„ā≥„ÉÉ„ÉČ„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„āí„Āē„āČ„ĀęŚćėÁīĒŚĆĖ„Āó„Āü„āā„Āģ„āíŤÄÉś°ą„Āó„Āü„Äā„É©„É≥„āį„Éą„É≥„Āģ„Éę„Éľ„Éó„Ā®ŚĎľ„Āį„āĆ„ÄĀ„ĀĮ„āč„Āč„ĀęŚįĎ„Ā™„ĀĄ„āĽ„Éęśēį„Āߍᙌ∑ĪŤ§áŤ£Ĺś©üŤÉĹ„āíŚģüÁŹĺ„Āó„Ā¶„ĀĄ„āč„ĀĆ„ÄĀŤ®ąÁģó„Ā®śßčÁĮČ„ĀģšłáŤÉĹśÄß„ĀĮŚ§Ī„āŹ„āĆ„Ā¶„ĀĄ„āč[4]„Äā ŚźĄÁ®ģCA„ĀģśĮĒŤľÉ
šĽēśßė „ā≥„ÉÉ„ÉČ„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„ĀĮŚõ썼ʌĮĺÁßįśÄß„Āģ„Āā„āč4ŤŅĎŚāćÔľą„Éē„ā©„É≥„ÉĽ„Éé„ā§„Éě„É≥ŤŅĎŚāćԾȄÄĀ8Áä∂śÖč„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„Āß„Āā„āč„Äā„ĀĚ„Āģ„ā≥„É≥„āĽ„Éó„Éą„ĀĮÁ©ļ„Āģ„Éē„ā£„Éľ„Éę„ÉČ(0)šłä„ĀģÁĶĆŤ∑Į(1)„ĀęŚüļ„Ā•„ĀĄ„Ā¶„ĀĄ„āč„ÄāÁĶĆŤ∑Į„ĀĮšŅ°ŚŹ∑„ĀģťÄö„āčŚįéÁ∑ö„Āß„Āā„āä„ÄĀ4„Āč„āČ7„ĀģÁä∂śÖč„Āßśßčśąź„Āē„āĆ„ÄĀŚĺĆ„āć„Āę„ĀĮ 1 ŚÄč„ĀģÁä∂śÖč0„Āģ„āĽ„Éę„ĀĆÁĹģ„Āč„āĆ„Ā¶ŤĽĘťÄĀ„ĀģśĖĻŚźĎ„āíŚģöÁĺ©„Āó„Ā¶„ĀĄ„āč„ÄāšŅ°ŚŹ∑„ĀĆÁ©ļ„Āģ„Éē„ā£„Éľ„Éę„ÉČÔľąÁä∂śÖč0„ĀßśļÄ„Āü„Āē„āĆ„ĀüÁ©ļťĖďԾȄĀęśľŹ„āĆŚáļ„Āô„Āģ„āíťė≤„Āź„Āü„āĀ„ÄĀÁĶĆŤ∑Į„ĀģŚĎ®Śõ≤„ĀĮÁä∂śÖč2„ĀģÁ∑ö„ĀߍĘꍶ܄Āē„āĆ„Ā¶„ĀĄ„āč„Äā„Āď„Āģ„āą„ĀÜ„Ā™Śüļśú¨śßčśąź„ĀĮ„ĀĚ„ĀģŚĺĆ„ĀģŚ§ö„ĀŹ„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥„Āß„āāśé°ÁĒ®„Āē„āĆ„Ā¶„ĀĄ„āč„Äāšĺč„Āą„Āį„ÄĀ„ÉĮ„ā§„ɧ„ÉĮ„Éľ„Éę„ÉČ„Ā™„Ā©„ĀĆ„Āā„āč„Äā ś¨°„ĀģŤ°®„ĀĮ„ÄĀśßė„ÄÖ„Ā™ś©üŤÉĹ„āíśĆĀ„Ā£„ĀüšŅ°ŚŹ∑Śąó„āíÁ§ļ„Āó„Ā¶„ĀĄ„āč„ÄāšłÄťÉ®„ĀģšŅ°ŚŹ∑Śąó„ĀĮŚįéÁ∑öŚÜÖ„Āß„ĀģŤ°ĚÁ™Ā„āíťė≤„Āź„Āü„āĀ„ÄĀŚįĎ„Ā™„ĀŹ„Ā®„āā2„āĽ„Éę„ĀģÁ©ļÁôĹÔľąÁä∂śÖč1ԾȄĀߌąÜťõĘ„Āē„āĆ„āčŚŅÖŤ¶Ā„ĀĆ„Āā„āč„Äā„ĀĚ„Āģ„Āü„āĀśú¨ť†ÖÁõģ„ĀģŚÜ흆≠„Āę„Āā„āčŚčēÁĒĽ„ĀĮ 'extend' „ĀģŚčēšĹú„āíÁ§ļ„Āó„Ā¶„ĀĄ„āč„ĀĆ„ÄĀšłč„ĀģŤ°®„Āß„ĀĮ„ĀĚ„āĆ„āíÔľąśúÄ„āāÁü≠„ĀĄÔľČ '70116011' „Ā®„Āó„Ā¶„ĀĄ„āč„Äā
„ā≥„É≥„ÉĒ„É•„Éľ„āŅ„ĀģśßčÁĮČ„ā≥„ÉÉ„ÉČ„ĀĮ„ÄĀWang„ĀģW„Éě„ā∑„É≥ (Wang B-machine) „ĀęŚüļ„Ā•„ĀĄ„Ā¶„ÄĀ„Āď„Āģ„āĽ„Éę„ÉĽ„ā™„Éľ„Éą„Éě„Éą„É≥šłä„Āߍᙌ∑ĪŤ§áŤ£Ĺ„Āô„āč„ā≥„É≥„ÉĒ„É•„Éľ„āŅ„ā퍮≠Ť®ą„Āó„Āü„Äā„Āó„Āč„Āó„ĀĚ„āĆ„ĀĮś•Ķ„āĀ„Ā¶Ś∑®Ś§ß„Ā™Ť®≠Ť®ą„Ā®„Ā™„āä„ÄĀTim Hutton „ĀĆ2009ŚĻī„ĀęśėéÁĘļ„Ā™śßčśąź„ĀßśßčÁĮČ„Āô„āč„Āĺ„ĀߌģüŤ£Ö„Āē„āĆ„Ā™„Āč„Ā£„Āü[5]„Äā„ĀĚ„ĀģťĀéÁ®č„ĀßHutton„ĀĮ„ā≥„ÉÉ„ÉČ„ĀģŤ®≠Ť®ą„ĀęŤč•ŚĻ≤„ĀģŤ™§„āä„ĀĆ„Āā„āč„Āď„Ā®„āíÁôļŤ¶č„Āó„Āü„Äā ŤĄöś≥®
ťĖĘťÄ£ť†ÖÁõģ
Ś§ĖťÉ®„É™„É≥„āĮ
|
Portal di Ensiklopedia Dunia













