|
クレンペラーのバラ飾り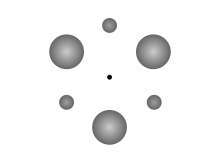 クレンペラーのバラ飾りは、重い天体と軽い天体が、共通の重心の周りで規則的な繰り返しの軌道で周回する重力系である。 1962年にWolfgang Klempererによって最初に記述された。 [1] クレンペラーは系を次のように説明した。 『このような対称性と独特な幾何学的配置によってバラ飾りと呼ばれるだろう。2つ(またはそれ以上)の偶数の「惑星」があり、1つ(またはいくつか)が他よりも重い天体で、等しい質量の各セットはすべて、2つ(またはそれ以上)の互いにかみ合う正多角形の角に配置される。そのため、より軽いものと重いものが交互に並んでい、(または循環的に互いに追従している)。』 最も単純なバラ飾りは、 菱形構成[重、軽、重、軽]で、互いに90度離れた4つの重い天体と軽い天体が交互に配置されている状態である。それぞれ同じ質量を持った重い天体2つと、軽い天体2つの組み合わせで構成されている。 配置パターンが周期的である限り、「質量」の種類を増やすことができる。例えば、[1,2,3 ... 1,2,3]、[1,2,3,4,5 ... 1,2,3,4,5]、[1,2,3,3,2,1 ... 1,2,3,3,2,1]など。 クレンペラーは八角形と菱形のバラ飾りについても言及した。 すべてのクレンペラーのバラ飾りは不安定化に対して脆弱であるが、六角形のバラ飾りは、互いのL4およびL5 ラグランジアンポイントに座っている「惑星」のため、特別な安定性を持っている。 誤用とスペルミス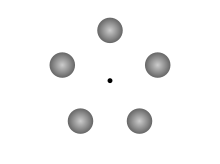 「クレンペラーのバラ飾り」(しばしばスペルミスされる「ケンペラーのバラ飾り/Kemplerer rosette」)という用語は、三個かそれ以上の等しい質量が、等辺多角形の頂点に置かれ、それらの重心の周りに等しい角速度を与えられた配置を意味するのによく用いられる。 クレンペラーは実際、この配置にかれの論文の出だしで触れているが、実際のばら飾りを提唱する前から存在する、既知の平衡系の一組に過ぎない。
不安定性この系のシミュレーション[2] (または単純な線形摂動解析)は、そのような系が不安定であることを示している。完全な幾何学的軌道から離れれば、振動が発生し、最終的に系の破壊につながる(クレンペラーの論文もこの事実を述べている)。 これはバラ飾りの中心が自由空間にあるか、それとも恒星の周りの軌道にあるか、いずれかでも起きる。 その理由は、摂動が対称性を破壊し、摂動が増加し、対称性がさらに損なわれるためである。 より長い説明は、接線方向の摂動が天体の隣にある天体に近づき、別の隣の天体から遠ざかる。重力の不均衡は、より近い隣の天体ほど大きくなり、より遠くの隣の天体ほど小さくなり、摂動を受けた物体をより近い隣に引き寄せ、摂動を減衰させるのではなく増幅させる。 内側の半径方向の摂動により、摂動が起こる物体に近づき、物体にかかる力が増加し、軌道速度が増加する。これにより、間接的に接線摂動と上記の理由が発生する。 参照資料
外部リンク |
Portal di Ensiklopedia Dunia