Rotazione stellare

L'aspetto deformato di Achernar (α Eridani) è causato dalla sua rapida rotazione.

La rotazione stellare è il movimento angolare di una stella sul proprio asse di rotazione. Il tempo di rotazione di una stella può essere misurato sulla base del suo spettro o cronometrando i movimenti delle strutture attive della sua superficie.

La rotazione della stella ha come effetto un rigonfiamento, posto nella regione equatoriale, dovuto alla forza centrifuga. Poiché le stelle non sono corpi solidi esse sono anche soggette ad una rotazione differenziale, perciò la velocità di rotazione equatoriale sarà diversa da quella delle latitudini più elevate. Tali differenze possono avere delle influenze significative sulla generazione del campo magnetico,[1] che tende spesso ad interagire con il vento stellare, causando un progressivo rallentamento della velocità di rotazione della stella.

Misurazioni

A meno che una stella non sia osservata in direzione del suo polo, ogni regione della sua superficie sembra avere dei determinati valori di movimento o in avvicinamento o allontanamento dall'osservatore. La componente del movimento che è in direzione con l'osservatore è detta velocità radiale. Quando la velocità radiale indica un avvicinamento all'osservatore, la radiazione subisce un aumento di frequenza (blueshift) dovuto all'effetto Doppler; se invece la velocità indica un allontantamento, la frequenza tende a diminuire (redshift). Tali effetti si riscontrano nell'osservazione degli spettri stellari, le cui linee di assorbimento poste ai limiti del tracciato spettrografico tendono ad allargarsi.[2] Tale allargamento va però accuratamente tenuto separato dagli altri effetti che possono causare un aumento nello spessore delle linee.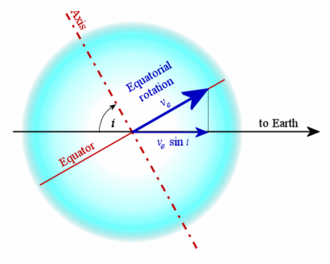

Questa stella ha un'inclinazione ${\displaystyle i}$ rispetto alla linea di vista di un osservatore sulla Terra ed una velocità di rotazione ${\displaystyle v_{e}}$ all'equatore.

La componente della velocità radiale osservata attraverso l'allargamento delle linee spettrali dipende dall'inclinazione del polo della stella sulla linea di vista dell'osservatore. Il valore che ne deriva è dato dalla formula

${\displaystyle v_{e}\cdot \sin i}$

dove ${\displaystyle v_{e}}$ è la velocità di rotazione all'equatore ed ${\displaystyle i}$ è l'inclinazione; quest'ultima però non è sempre conosciuta, per cui il risultato dà un valore minimo per la velocità di rotazione della stella. In altri termini, se ${\displaystyle i}$ non è un angolo retto, la velocità è sempre maggiore di ${\displaystyle v_{e}\cdot \sin i}$.[2]

Nelle stelle giganti le microturbolenze atmosferiche possono dar luogo a degli allargamenti delle linee spettrali decisamente maggiori di quelli causati solamente dagli effetti della rotazione, alterando notevolmente il segnale. Può essere anche impiegato un approccio alternativo, basato sull'effetto lente gravitazionale, che ha come risultato l'amplificazione dell'immagine della stella retrostante. Le informazioni più dettagliate che se ne ottengono permettono di distinguere gli effetti della microturbolenza da quelli della rotazione.[3]

Se una stella mostra tracce di attività magnetica superficiale, come le macchie stellari, queste possono essere rintracciate per stimare la velocità di rotazione. Le macchie possono però formarsi in luoghi diversi dall'equatore e possono migrare di latitudine nel corso della loro vita; la rotazione differenziale, cui è soggetta la stella, è in questo modo all'origine di misurazioni variabili. L'attività magnetica stellare è spesso associata alla rapida rotazione, pertanto questa tecnica può trovare impiego per le misurazioni delle stelle magneticamente attive.[4] Le osservazioni delle macchie hanno mostrato inoltre che tali caratteristiche possono variare la velocità di rotazione della stella, poiché il campo magnetico svolge un ruolo di primo piano nel plasmare i flussi di gas all'interno della stella.[5]

Effetti fisici

Rigonfiamento equatoriale

Raffronto tra Vega (a sinistra) e il Sole (a destra); da notare il pronunciato rigonfiamento equatoriale di Vega.

La rotazione di una stella produce una netta forza centrifuga in direzione perpendicolare all'asse di rotazione. Al polo essa si presenta pari a zero e non si oppone alla forza di gravità generata dalla stella; all'equatore invece la forza centrifuga non è uguale a zero e perciò si oppone parzialmente alla forza di gravità. Per poter bilanciare questo squilibrio di forze, la superficie stellare tende a rigonfiarsi in corrispondenza dell'equatore e la stella diviene uno sferoide oblato.

Un esempio peculiare di rigonfiamento equatoriale è riscontrabile in Regolo A (α Leonis A), la cui velocità di rotazione all'equatore è stata misurata in 317 ±3 km/s, che corrisponde ad un periodo di rotazione di 15,9 ore (l'86% della velocità raggiunta la quale una stella andrebbe incontro alla propria rottura). Il raggio equatoriale della stella è il 32% più largo del raggio polare.[6] Altre stelle caratterizzate da un'alta velocità di rotazione sono Alfa Arae, Vega ed Achernar.

La velocità di rottura di una stella è un'espressione utilizzata per descrivere il caso in cui la forza centripeta all'equatore sia identica alla forza gravitazionale; perché una stella sia stabile, la velocità di rotazione deve essere al di sotto di questa soglia.[7]

Rotazione differenziale

Le stelle, come il Sole, presentano sulla loro superficie una rotazione differenziale, che dipende dal variare, a seconda della latitudine, della velocità angolare. La velocità angolare tende normalmente a diminuire all'aumentare della latitudine, ma è stato recentemente osservato il contrario (come nella stella HD 31993).[8][9] La prima stella, dopo il Sole, cui è stata misurata la rotazione differenziale è AB Doradus.[10][11]

Il meccanismo alla base della rotazione differenziale è la turbolenta convezione del gas all'interno della stella; i moti convettivi trasportano energia alla superficie tramite i movimenti della massa di plasma, che a sua volta possiede una parte della velocità angolare della stella. Quando si verifica una turbolenza a causa della rotazione, il momento angolare subisce una ridistribuzione a differenti latitudini a causa del cosiddetto flusso meridionale.[12][13]

Si ritiene che le zone di transizione tra le regioni con spiccate differenze nella velocità di rotazione siano quelle in cui si verificano i "fenomeni dinamo" all'origine del campo magnetico. Quest'ultimo tende ad interagire, in maniera estremamente complessa, con la distribuzione della rotazione della stella; in questo modo l'energia magnetica viene convertita in energia cinetica, che va a modificare la distribuzione della velocità.[11]

Rallentamenti della velocità di rotazione

Le moderne teorie sulla formazione stellare sostengono che le stelle si formino dal collasso gravitazionale di una nube molecolare a bassa temperatura costituita da gas e polveri. Man mano che il collasso prosegue, la conservazione del momento angolare provoca un netto aumento della rotazione della nube, costringendo la materia in un disco attorno alla neoformata protostella, che si riscalda a causa dell'energia potenziale gravitazionale dovuta al collasso.

Velocità
di rotazione
media[14]

Classe spettrale	ve (km/s)
O5	190
B0	200
B5	210
A0	190
A5	160
F0	95
F5	25
G0	12

Il continuo collasso può portare ad un aumento della velocità di rotazione della protostella in accrescimento, al punto che essa può arrivare a rompersi a causa della grande forza centrifuga all'equatore; per evitare questo scenario la protostella deve frenare nei suoi primi 150 000 anni di vita tale velocità di rotazione.

Una possibile spiegazione a tale rallentamento è fornita dall'interazione tra il campo magnetico ed il vento stellare; l'espansione di quest'ultimo preleva via una parte del momento angolare e rallenta la rotazione della protostella in fase di collasso.[15][16]

È stato scoperto che gran parte delle stelle di sequenza principale con una classe spettrale compresa tra O5 ed F5 ruoti a velocità elevatissime;[6][17] si è anche notato che la velocità di rotazione, in queste stelle, cresce all'aumentare della massa, con un picco tra le giovani e massicce stelle di classe B. Come la durata della vita di una stella diventa minore man mano che la massa aumenta, così si ritiene che la velocità di rotazione della stella diminuisca con l'avanzare dell'età.

La diminuzione della rotazione delle stelle di sequenza principale può essere riassunta dalla relazione matematica:

${\displaystyle \Omega _{e}\propto t^{-{\frac {1}{2}}}}$

dove ${\displaystyle \Omega _{e}}$ è la velocità angolare all'equatore e ${\displaystyle t}$ è l'età della stella.[18] Tale relazione prende il nome di legge di Skumanich, dal nome dell'astrofisico Andrew P. Skumanich che la scoprì nel 1972.[19] La girocronologia è la disciplina che determina l'età di una stella a partire dalla sua velocità di rotazione.[20]

Le stelle perdono lentamente una parte della propria massa tramite l'emissione del vento stellare dalla fotosfera, su cui esercita un momento meccanico che determina un costante trasferimento verso l'esterno del momento angolare della stella. Le stelle che presentano una velocità di rotazione superiore a 15 km/s mostrano una maggiore perdita di massa e di conseguenza un più marcato rallentamento della velocità di rotazione. Così, mentre diminuisce gradualmente la velocità di rotazione della stella, si ha anche una diminuzione nella perdita del momento angolare. In queste condizioni la stella tende ad avvicinarsi, senza però mai raggiungerla, alla condizione ${\displaystyle v_{e}=0}$.[21]

Sistemi binari stretti

Un "sistema binario stretto" è una particolare tipologia di sistema stellare binario in cui le due componenti orbitano l'una attorno all'altra ad una distanza media dello stesso ordine di grandezza del loro diametro. A tali distanze possono intervenire delle interazioni più complesse, come forze mareali, trasferimenti di massa e persino collisioni.

Le interazioni mareali possono provocare un cambiamento dei parametri orbitali e rotativi: infatti mentre il momento angolare totale del sistema rimane invariato, il momento angolare di ciascuna componente può essere trasferito tra il periodo orbitale e la velocità di rotazione.[22]

Ciascuno dei membri di un sistema binario stretto esercita sull'altro una forte attrazione gravitazionale, ma i rigonfiamenti da essa causati possono non essere perfettamente allineati con la direzione della forza di gravità; perciò la forza gravitazionale esercita una componente di coppia, che comporta un trasferimento del momento angolare. Questo fa sì che il sistema vada incontro ad una continua evoluzione, anche se attraversano una fase di equilibrio stabile. L'effetto può essere più complesso nel caso in cui l'asse di rotazione non sia perpendicolare al piano orbitale.[22]

Per le binarie a contatto o semi-separate, il trasferimento di massa da una stella alla compagna può anche comportare un significante trasferimento di momento angolare. La componente in fase di accrescimento può arrivare al punto in cui raggiunge la sua velocità critica di rotazione ed inizia a perdere massa lungo l'equatore.[23]

Stelle degeneri

Quando una stella finisce di generare energia tramite la fusione nucleare essa si evolve sino ad uno stadio compatto e degenere. Durante questa fase le dimensioni della stella subiscono una riduzione significativa; tale riduzione spesso corrisponde ad un aumento della velocità angolare.

Nane bianche

Una nana bianca è una stella costituita dai prodotti del processo di fusione nucleare sintetizzati durante le ultime fasi della vita della stella, ma è priva della massa necessaria per fonderli in elementi più pesanti. Si tratta di un corpo compatto mantetenuto stabile dall'equilibrio che sussiste tra il collasso gravitazionale ed un effetto quantistico noto come pressione degenerativa degli elettroni. Normalmente le nane bianche hanno una velocità di rotazione piuttosto bassa, spesso per via della altrettanto lenta rotazione che la stella progenitrice aveva al momento in cui ha perso i suoi strati esterni, trasformandosi in nebulosa planetaria.[24]

Una nana bianca che ruota lentamente non può superare il limite di Chandrasekhar di 1,44 masse solari senza poi collassare in una stella di neutroni o esplodere come una supernova di tipo Ia; qualora la stella raggiungesse questa massa critica, ad esempio tramite l'accrescimento a spese di una gigante rossa in un sistema binario o la collisione con un'altra stella, la forza gravitazionale riuscirebbe a sovrastare la pressione degli elettroni. Se però la nana bianca ruota velocemente la forza centripeta all'equatore può controbilanciare la gravità e permettere alla stella di superare "agevolmente" il limite di Chandrasekhar. Una simile rotazione rapida può verificarsi, ad esempio, nel caso in cui l'accrescimento della massa della nana bianca abbia come risultato secondario il trasferimento di una certa quantità di momento angolare.[25]

Stelle di neutroni

La stella di neutroni (al centro) emette dai suoi poli magnetici un fascio di radiazioni, strutturato secondo uno schema conico posto attorno all'asse di rotazione.

Una stella di neutroni è un residuo stellare altamente denso, costituito essenzialmente da neutroni — particelle (nucleoni) del nucleo atomico prive di carica elettrica — la cui massa è compresa tra 1,35 e 2,1 masse solari. Come risultato del collasso, una stella di neutroni appena formata può avere un'altissima velocità di rotazione che può portarla a compiere alcune migliaia di rotazioni al secondo.[26]

Una particolare tipologia di stelle di neutroni dotate di campo magnetico sono le pulsar, dai cui poli magnetici cui si diparte uno stretto fascio di radiazioni elettromagnetiche. Se questo fascio di radiazioni è orientato in direzione del Sistema solare, la pulsar verrebe percepita da Terra come una serie di periodiche "pulsazioni" nella radiazione. L'energia irradiata dal campo magnetico gradualmente rallenta la rotazione della pulsar, al punto che le pulsar più vecchie arrivano a generare una sola pulsazione al secondo.[27]

Buchi neri

Un buco nero è un oggetto il cui campo gravitazionale è talmente forte da non far sfuggire nemmeno la luce.

Al momento della loro formazione, a causa del collasso di una grande massa in rotazione, mantengono il proprio momento angolare, che ha come effetto la costrizione dello spazio attorno al buco nero in un volume sferoidale oblato detto ergosfera. La massa in caduta all'interno di questo volume acquisisce energia e può essere espulsa lungo l'asse di rotazione del buco nero senza essere da esso inghiottita; questo processo comporta però una perdita di momento angolare da parte del buco nero.[28] La velocità di rotazione di un buco nero possiede dei valori vicini alla velocità della luce.[29]

Note

1. Jean-François Donati, Differential rotation of stars other than the Sun, su ast.obs-mip.fr, Laboratoire d'Astrophysique de Toulouse, 5 novembre 2003. URL consultato il 24 giugno 2007.
2. G. Shajn, O. Struve, On the rotation of the stars, in Monthly Notices of the Royal Astronomical Society, vol. 89, 1929, pp. 222-239. URL consultato il 25 giugno 2007.
3. Andrew Gould, Measuring the Rotation Speed of Giant Stars from Gravitational Microlensing, in Astrophysical Journal, vol. 483, 1997, pp. 98-102. URL consultato il 28 giugno 2007.
4. W. Soon, P. Frick, S. Baliunas, On the rotation of the stars, in The Astrophysical Journal, vol. 510, n. 2, 1999, pp. L135-L138. URL consultato il 25 giugno 2007.
5. A. Collier Cameron, J.-F. Donati, Doin' the twist: secular changes in the surface differential rotation on AB Doradus, in Monthly Notices of the Royal Astronomical Society, vol. 329, n. 1, 2002, pp. L23-L27. URL consultato il 25 giugno 2007.
6. H. A. McAlister, T. A. ten Brummelaar, et al., First Results from the CHARA Array. I. An Interferometric and Spectroscopic Study of the Fast Rotator Alpha Leonis (Regulus)., in The Astrophysical Journal, vol. 628, 2005, pp. 439-452.
7. J. Hardorp, P. A. Strittmatter, Rotation and Evolution of be Stars, in Proceedings of IAU Colloq. 4, Gordon and Breach Science Publishers, Ohio State University, Columbus, Ohio, 8-11 settembre 1969, p. 48. URL consultato il 26 giugno 2007.
8. L. L. Kitchatinov, G. Rüdiger, Anti-solar differential rotation, in Astronomische Nachrichten, vol. 325, n. 6, 2004, pp. 496-500. URL consultato il 27 giugno 2007.
9. G. Rüdiger, B. von Rekowski, R. A. Donahue, S. L. Baliunas, Differential Rotation and Meridional Flow for Fast-rotating Solar-Type Stars ^[collegamento interrotto], in Astrophysical Journal, vol. 494, 1998, pp. 691-699. URL consultato il 27 giugno 2007.
10. J.-F. Donati, A. Collier Cameron, Differential rotation and magnetic polarity patterns on AB Doradus, in Monthly Notices of the Royal Astronomical Society, vol. 291, n. 1, 1997, pp. 1-19. URL consultato il 3 luglio 2007.
11. Jean-François Donati, Differential rotation of stars other than the Sun, su ast.obs-mip.fr, Laboratoire d'Astrophysique de Toulouse, 5 novembre 2003. URL consultato il 24 giugno 2007.
12. Holly Korab, NCSA Access: 3D Star Simulation, su access.ncsa.uiuc.edu, National Center for Supercomputing Applications, 25 giugno 1997. URL consultato il 27 giugno 2007 (archiviato dall'url originale il 1º maggio 2012).
13. M. Küker, G. Rüdiger, Differential rotation on the lower main sequence, in Astronomische Nachrichten, vol. 326, n. 3, 2004, pp. 265-268. URL consultato il 27 giugno 2007.
14. D. McNally, The distribution of angular momentum among main sequence stars, in The Observatory, vol. 85, 1965, pp. 166-169. URL consultato il 26 giugno 2007.
15. J. Ferreira, G. Pelletier, S. Appl, Reconnection X-winds: spin-down of low-mass protostars, in Monthly Notices of the Royal Astronomical Society, vol. 312, 2000, pp. 387-397. URL consultato il 26 giugno 2007.
16. Terry Devitt, What Puts The Brakes On Madly Spinning Stars?, su news.wisc.edu, University of Wisconsin-Madison, 31 gennaio 2001. URL consultato il 27 giugno 2007.
17. Deane M. Peterson et al, Resolving the effects of rotation in early type stars. New Frontiers in Stellar Interferometry, Proceedings of SPIE Volume 5491, in The International Society for Optical Engineering, Bellingham, Washington, USA, 2004, p. 65. URL consultato il 25 giugno 2007.
18. Jean-Louis Tassoul, Stellar Rotation (PDF), Cambridge, MA, Cambridge University Press, 1972, ISBN 0-521-77218-4.
19. Andrew P. Skumanich, Time Scales for CA II Emission Decay, Rotational Braking, and Lithium Depletion, in The Astrophysical Journal, vol. 171, 1972, p. 565.
20. Gyrochronology, su astrobio.net, Astrobiology Magazine, 29 aprile 2007. URL consultato il 26 giugno 2007 (archiviato dall'url originale il 29 settembre 2007).
21. Kyoji Nariai, Mass Loss from Coronae and Its Effect upon Stellar Rotation, in Astrophysics and Space Science, vol. 3, 1969, pp. 150-159. URL consultato il 27 giugno 2007.
22. P. Hut, Tidal evolution in close binary systems, in Astronomy and Astrophysics, vol. 99, n. 1, 1999, pp. 126-140. URL consultato il 7 giugno 2007.
23. D. Weaver, M. Nicholson, One Star's Loss is Another's Gain: Hubble Captures Brief Moment in Life of Lively Duo, su hubblesite.org, NASA Hubble, 4 dicembre 1997. URL consultato il 3 luglio 2007.
24. L. A. Willson, R. Stalio, Angular Momentum and Mass Loss for Hot Stars (1ª edizione), Springer, 1990, ISBN 0-7923-0881-6.
25. S.-C Yoon, N. Langer, Presupernova evolution of accreting white dwarfs with rotation, in Astronomy and Astrophysics, vol. 419, 2004, pp. 623-644. URL consultato il 3 luglio 2007.
26. J. Lochner, M. Gibb, Neutron Stars and Pulsars, su imagine.gsfc.nasa.gov, NASA, dicembre 2006. URL consultato il 27 giugno 2007.
27. D. R. Lorimer, Binary and Millisecond Pulsars, su relativity.livingreviews.org, Max-Planck-Gesellschaft, 28 agosto 1998. URL consultato il 27 giugno 2007 (archiviato dall'url originale il 1º maggio 2012).
28. Mitchell C. Begelman, Evidence for Black Holes, in Science, vol. 300, n. 5627, 2003, pp. 1898-1903. URL consultato il 26 giugno 2007.
29. Lee Tune, Spin of Supermassive Black Holes Measured for First Time, su newsdesk.umd.edu, University of Maryland Newsdesk, 29 maggio 2007. URL consultato il 25 giugno 2007 (archiviato dall'url originale il 21 giugno 2007).

Voci correlate

• Campo magnetico stellare
• Struttura stellare

Collegamenti esterni

• (EN) Stellar Spots and Cyclic Activity: Detailed Results - ETH Zentrum, su saturn.ethz.ch. URL consultato il 9 febbraio 2008 (archiviato dall'url originale il 16 marzo 2008).

Controllo di autorità	LCCN (EN) sh85127449 · GND (DE) 4243974-7