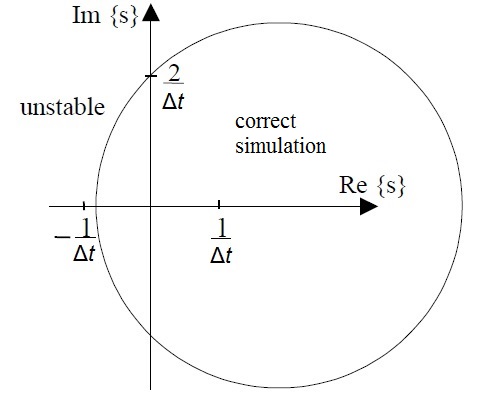
Metodo di Eulero semi-implicito

In matematica il metodo di Eulero semi-implicito, detto anche Eulero simplettico, Eulero semi-esplicito, Eulero-Cromer[1], e Newton-Størmer-Verlet (NSV), è una variante del metodo di Eulero usato per risolvere equazioni di Hamilton. È un integratore simplettico, pertanto consente di ottenere risultati migliori rispetto al metodo di Eulero semplice.

Impostazione del problema

Il metodo può essere applicato ad una coppia di equazioni differenziali nella forma

${\displaystyle {dx \over dt}=f(t,v)}$

${\displaystyle {dv \over dt}=g(t,x)}$

dove ${\displaystyle f}$ e ${\displaystyle g}$ sono funzioni date e ${\displaystyle x}$ e ${\displaystyle v}$ possono essere vettori o scalari. Le equazioni di Hamilton assumono questa forma se la funzione hamiltoniana ha la forma

${\displaystyle H=T(t,v)+V(t,x)}$

Inoltre le condizioni iniziali devono essere note:

${\displaystyle x(t_{0})=x_{0}}$

${\displaystyle v(t_{0})=v_{0}}$

Formulazione del metodo

Il metodo produce una soluzione discreta approssimata iterando le seguenti funzioni:

${\displaystyle v_{n+1}=v_{n}+g(t_{n},x_{n})\Delta t}$

${\displaystyle x_{n+1}=x_{n}+f(t_{n},v_{n+1})\Delta t}$

dove ${\displaystyle \Delta t}$ è l'intervallo di tempo e ${\displaystyle t_{n}=t_{0}+n\Delta t}$ è il tempo dopo ${\displaystyle n}$ iterazioni.

La differenza con il metodo di Eulero classico consiste nel fatto che il metodo semi-implicito usa ${\displaystyle v_{n+1}}$ nell'equazione per ${\displaystyle x_{n+1}}$, mentre il metodo classico usa ${\displaystyle v_{n}}$.

Utilizzando il metodo con un intervallo di tempo negativo per calcolare ${\displaystyle (x_{n},v_{n})}$ da ${\displaystyle (x_{n+1},v_{n+1})}$ consente di ottenere la seconda variante del metodo di Eulero semi-implicito:

${\displaystyle x_{n+1}=x_{n}+f(t_{n},v_{n})\Delta t}$

${\displaystyle v_{n+1}=v_{n}+g(t_{n},x_{n+1})\Delta t}$

la quale presenta simili proprietà.

Il metodo di Eulero semi-implicito, come quello classico, è un integratore del primo ordine: ciò significa che produce un errore dell'ordine di Δt. Tuttavia, a differenza del metodo classico, quello semi-implicito è un integratore simplettico, perciò conserva quasi inalterata l'energia (se la funzione hamiltoniana è indipendente dal tempo), mentre nel metodo classico essa aumenta costantemente.

Alternare le due varianti del metodo semi-implicito conduce, in una forma semplificata, all'integrazione di Størmer-Verlet e in un'altra forma semplificata al metodo del salto della rana, aumentando sia l'ordine dell'errore che quello della conservazione dell'energia.

Il metodo di Eulero semi-implicito rappresenta correttamente il sistema simulato se le radici complesse dell'equazione caratteristica si trovano all'interno di questa circonferenza:

Come si può vedere, il metodo è in grado di simulare correttamente sia sistemi stabili che instabili. Ciò costituisce un vantaggio rispetto al metodo classico e a quello implicito.

Esempio

Il moto di una molla, seguendo la legge di Hooke, si può rappresentare come:

${\displaystyle {\frac {dx}{dt}}=v(t)}$

${\displaystyle {\frac {dv}{dt}}=-{\frac {k}{m}}x=-\omega ^{2}x}$

Il metodo di Eulero semi-implicito in questo caso è:

${\displaystyle v_{n+1}=v_{n}-\omega ^{2}x_{n}\Delta t}$

${\displaystyle x_{n+1}=x_{n}+v_{n+1}\Delta t}$

Sostituendo ${\displaystyle v_{n+1}}$ nella seconda equazione con l'espressione data dalla prima equazione, l'iterazione può essere espressa nella seguente forma matriciale:

${\displaystyle {\begin{bmatrix}x_{n+1}\\v_{n+1}\end{bmatrix}}={\begin{bmatrix}1-\omega ^{2}\Delta t^{2}&\Delta t\\-\omega ^{2}\Delta t&1\end{bmatrix}}{\begin{bmatrix}x_{n}\\v_{n}\end{bmatrix}}}$

Note

1. (EN) Alan Cromer, Stable solutions using the Euler approximation (abstract), in The American Journal of Physics, vol. 49, n. 5, 1981, pp. 455-459.

Bibliografia

• (EN) Franz J. Vesely, Computational Physics: An Introduction, 2nd, Springer, 2001, pp. 117, ISBN 978-0-306-46631-1.

Voci correlate

• Metodi di soluzione numerica per equazioni differenziali ordinarie
• Metodo di Eulero
• Metodo di Eulero all'indietro
• Equazione differenziale ordinaria
• Meccanica hamiltoniana

Collegamenti esterni

• (EN) Branislav K. Nikolic, Euler-Cromer method, su physics.udel.edu, University of Delaware. URL consultato il 29 settembre 2021.